Veranderingen per stap

Inleiding

Om veranderingen van grafieken nauwkeurig te beschrijven kijk je naar de toenames (of afnames) van de uitkomsten bij toename van de invoerwaarden met een vaste stapgrootte.
Bijvoorbeeld bij een functie y = f(x) bekijk je de toename van y bij een toename van x met een vaste stapgrootte. Je maakt van die toenames een toenamediagram.

Je leert nu:

een toenamediagram maken bij een gegeven grafiek of een gegeven functievoorschrift;
de invloed van de stapgrootte op het toenamediagram;
vanuit een gegeven toenamediagram (en 'beginwaarde') een mogelijke grafiek van de functie samenstellen.

Je kunt al:

grafieken van functies tekenen en in beeld brengen met bijvoorbeeld de grafische rekenmachine;
werken met functievoorschriften, functiewaarden berekenen;
(toenemende, of afnemende, of constante) stijging en daling, maximum en minimum herkennen.

Verkennen

Via www.getij.nl, een website van het Ministerie van Verkeer en waterstaat, vind je een grafiek van de waterstand bij Vlissingen.

Om een beetje nauwkeuriger zicht te krijgen op de veranderingen van de waterstand, kun je ook een staafdiagram maken van de veranderingen per uur.

Maak zo'n staafdiagram.
Hoe kun je aan het staafdiagram zien of het water stijgt of daalt?
Hoe kun je aan dat staafdiagram zien wanneer het water snel stijgt?
In de Westerschelde moet je goed weten waar je wel en waar je niet kunt varen. Wat heb je dan aan het diagram met veranderingen van de waterstand?

Uitleg

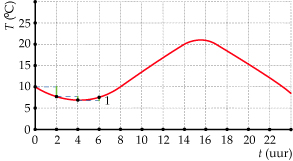
Deze grafiek geeft de gemiddelde dagtemperatuur T op een bepaalde plaats (in °C) weer afhankelijk van het tijdstip t (in uren) op de dag.

De grafiek begint op t = 0 met een temperatuur van 10°C.
Na 2 uur is die temperatuur gezakt tot ongeveer 8°C.
Er is bij t = 2 sprake van een toename van –2°C.

Weer twee uur later is de temperatuur nog een graad gezakt: bij t = 4 is sprake van een toename van –1°C ten opzichte van de temperatuur bij t = 2.

En zo kun je doorgaan met het bepalen van de toenames (of afnames) in stappen van 2 uur. Je doorloopt de tijd met een stapgrootte van 2 uur en je maakt een tabel van toenames:

t (uur)	0	2	4	6	8	10	12	14	16	18	20	22	24
ΔT		–2	–1	1	2	3	3,5	3,5	1	–3	–2	–3,5	–3,5

Onder ΔT versta je de toename van de temperatuur T.
Deze tabel kun je weergeven in een diagram.

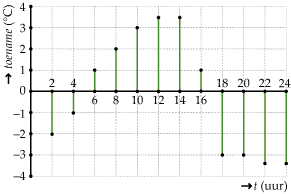
Deze tabel kun je weergeven in een diagram.
Zo'n diagram noem je toenamendiagram.

In het toenamendiagram kun je goed zien

waar de grafiek stijgend is, zijn de toenamen positief (echte toenamen);
waar de grafiek dalend is, zijn de toenamen negatief (eigenlijk afnamen);

En waar de toenamen steeds groter worden is de stijging toenemend, etc.

‡

Opgaven

Bekijk de grafiek van de gemiddelde dagtemperatuur in de Uitleg.
1. Maak zelf een tabel met 'toenames' vanaf `t=0` met een stapgrootte van Δt = 3.
2. Teken zelf het toenamendiagram van de temperatuurgrafiek met een stapgrootte van Δt = 3.

Theorie

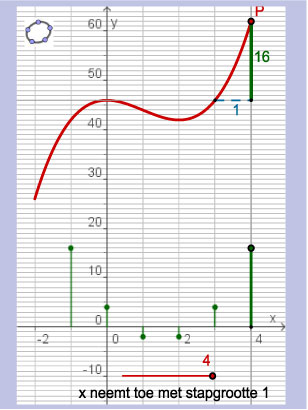
Hier zie je de grafiek van een functie y = f(x) op [–2,4].
Als je de waarden van x met een vaste stapgrootte h laat toenemen, kun je daarbij een tabel maken van de toenames Δy van de functiewaarden.

Als h = 1 dan ziet die tabel er zo uit:

x	–2	–1	0	1	2	3	4
y	26	42	46	44	42	46	64
Δy		16	4	–2	–2	4	16

Het toenamendiagram maak je hiernaast.
Telkens is de toename van de functie Δ`y=f(x)-f(x-h)`.
Bij h = 1 geldt daarom voor de toenames Δ`y=f(x)-f(x-1)`.
En dat laatste is weer handig als je het functievoorschrift weet.

Je kunt dan je GR gebruiken en invoeren Y1=f(X) en Y2=Y1(X)–Y1(X–1), waarin f de gegeven functie is. En dat levert een toenametabel op.
Een toenamediagram zoals dat hiernaast kan de rekenmachine niet maken.

‡

Voorbeeld 1

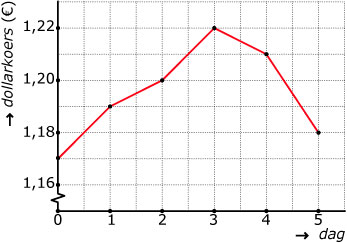
Hier zie je de grafiek van het verloop van de koers van de dollar. Maak er een toenamediagram bij met stapgrootte 1 dag.

Antwoord

Maak eerst een tabel met toenames.

dag	0	1	2	3	4	5
toename (cent)		2	1	2	–1	–3

Zet vervolgens deze toenames verticaal uit.

‡

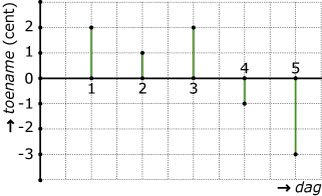
Voorbeeld 2

Gegeven de functie met voorschrift y = x² op het interval [–3,3].
Maak het toenamediagram bij deze functie met stapgrootte 1.

Antwoord

Hieronder zie je hoe je met de rekenmachine een toenametabel maakt bij een stapgrootte van 1.

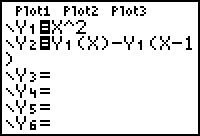
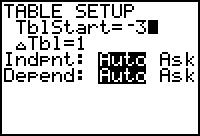
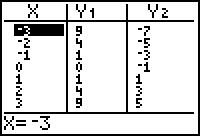
Maak daarbij een toenamediagram.

‡

Voorbeeld 3

Bekijk hoe je uit een toenamediagram een grafiek kunt samenstellen.

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Veranderingen > Per stap > Voorbeeld 3

‡

Opgaven

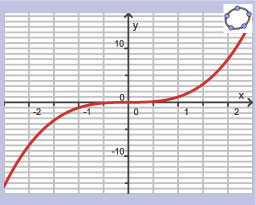
In Voorbeeld 1 zie je hoe je een toenamediagram maakt bij een gegeven grafiek.
Je ziet hier de grafiek van een functie. Je laat de waarden van `x` oplopen met een stapgrootte 1. De bijbehorende verandering van de functiewaarden kun je in een tabel zetten.
1. Maak een toenametabel die begint bij `x=-2`.
2. Teken het bijpassende toenamediagram.

Maak op je grafische rekenmachine de grafiek van de functie van `f` met voorschrift `f(x)=-x^3+6*x` op het interval `[-3,3]`.
1. Met de grafische rekenmachine kun je een toenametabel met stapgrootte 1 laten maken. In Voorbeeld 2 zie je hoe dat gaat.
  Maak een toenametabel die begint bij `x=-3`.
2. Wat weet je op grond van alleen de toenametabel van het maximum van deze functie?
  1. Dat zit tussen `x=0` en `x=1` want bij die waarden horen dezelfde toenamen.
  2. Dat zit tussen `x=0` en `x=1` want bij die waarden horen de grootste toenamen.
  3. Dat zit bij `x=1,5` want precies daar gaan de toenamen over in afnamen.
  4. Tussen `x=1` en `x=2` want bij die waarden gaan de toenamen over van positief in negatief.
3. Teken het bijpassende toenamediagram.

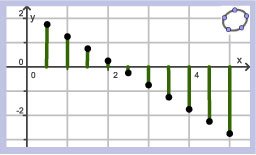Je ziet hier het toenamediagram van een functie `f`.
Schets een mogelijke grafiek van `f`.

Hier zie je het toenamediagram van de grafiek van een functie `f` waarvoor geldt: `f(0)=4`.
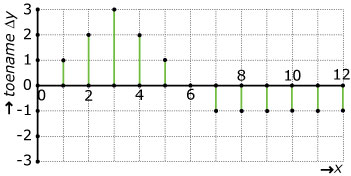
1. Maak nu een grafiek van functie `f`, bekijk Voorbeeld 3 nog maar eens
2. Je kunt wel een mogelijke grafiek van `f` tekenen. Maar waarom zijn er nog meerdere mogelijkheden?
  1. Het toenamediagram is te onduidelijk om functiewaarden nauwkeurig uit af te lezen.
  2. Omdat een toenamediagram een vaste stapgrootte heeft kun je geen tussenliggende functiewaarden bepalen.
  3. Er zijn meerdere toenametabellen mogelijk bij dit toenamediagram.

Verwerken

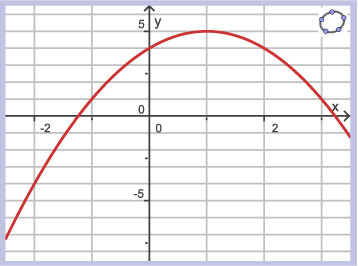Dit is een deel van de grafiek van een functie.
Teken bij deze grafiek een toenamediagram met stapgrootte `1`, te beginnen bij `x=-2`.

Gegeven is de functie `f` met voorschrift `f(x)=0,5*x^4-4x^2+8`.
1. Met de grafische rekenmachine kun je de grafiek van deze functie bekijken en een toenametabel maken. Teken een toenamediagram op het interval `[-3,3]` met een stapgrootte van `0,5`.
2. Er is precies één interval waarop de grafiek toenemend daalt. Welk interval is dat? En hoe zie je dat aan het toenamediagram?
3. Waarom kun je op grond van het toenamediagram concluderen dat er waarschijnlijk drie extremen zijn?

In een pretpark is vanaf de opening om 8:00 uur ’s morgens tot de sluitingstijd om 18:00 uur elk uur het aantal ingaande en uitgaande bezoekers geteld. Het verschil van beide is de toename (of afname) van het aantal bezoekers. Hier zie je deze toename weergegeven.
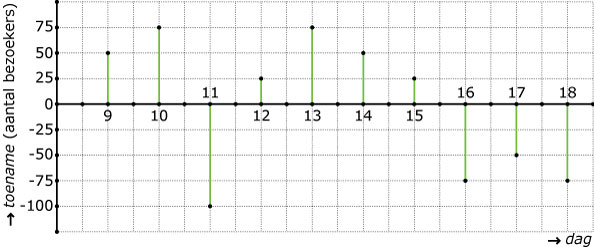
1. Maak nu een grafiek van het totaal aantal bezoekers afhankelijk van het uur van deze dag, vanaf 8:00 uur tot en met 18:00 uur.
2. Rond welk tijdstip waren er waarschijnlijk de meeste bezoekers in het pretpark?
3. Kun je vaststellen hoeveel bezoekers er maximaal in het park waren op enig moment die dag?
  Licht je antwoord toe.

Biologen houden het verloop van de aantallen van een bepaald soort vlinder in een afgesloten natuurgebied bij. Deze tabel geeft de verzamelde informatie weer.

Jaartal	2000	2001	2002	2003	2004
Aantal vlinders	2450	2050	1850	1665	1580
Verschil t.o.v. voorgaande jaar		–400	–240	–145	–85

Het lijkt erop dat het verschil `V` t.o.v. het voorgaande jaar exponentieel verandert met de tijd `t` in jaren. Er lijkt te gelden `V=-400*0,6^(t-1)` met `t = 0` in het jaar 2000.

Ga na of deze formule in overeenstemming is met de gevonden verschillen.
Ga er van uit dat deze formule geldig blijft in de jaren na 2004. Teken een toenamediagram van het aantal vlinders in dit natuurgebied met een stapgrootte van 1 jaar.
Maak ook een grafiek van het aantal vlinders `N` in de loop van de jaren.
Van wat voor soort daling is er sprake bij het aantal vlinders? Hoe kun je dat aan het toenamediagram zien?
Het aantal vlinders van deze soort lijkt zich in dit natuurgebied te stabiliseren. Hoe kun je dat aan het toenamediagram zien? En wat betekent dit voor de grafiek van het aantal vlinders?

Testen

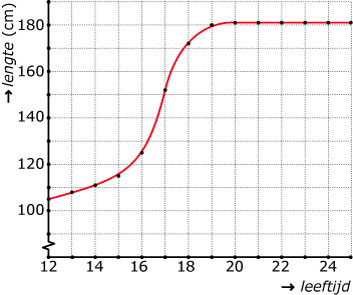Je ziet hier de grafiek van de lengte van een man vanaf zijn twaalfde levensjaar tot zijn huidige leeftijd.
1. Maak bij deze grafiek een toenamediagram met een stapgrootte van 1 jaar.
2. Hoe kun je aan het toenamediagram zien dat de grafiek nooit dalend is?
3. Waarom mag je op grond van het toenamediagram alleen nooit de conclusie trekken dat de grafiek nooit dalend is?
4. Gedurende welke periode is zijn lengte constant? Hoe zie je dat aan het toenamediagram?
5. Gedurende welke perioden is de groeisnelheid constant? Hoe zie je dat aan het toenamediagram?

Bekijk met je grafische rekenmachine de grafiek van de functie `f(x)=-0,5*x^4+4*x^2` op het interval `[-4,4]`.
1. Teken een toenamediagram met een stapgrootte van `0,5`.
2. Opwelk interval is er sprake van een afnemende daling? Hoe zie je dat aan het toenamediagram?
3. Hoe kun je in het toenamediagram de plaats van de extremen van de functie terugvinden?

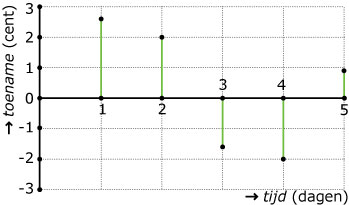De Amerikaanse dollar stond dinsdag op een koers van € 1,220. De figuur heeft betrekking op dezelfde week van zondag tot en met vrijdag. In de figuur zie je de toename of afname van de koers per dag in tienden van centen nauwkeurig.

Teken een grafiek waarin de koers van de dollar in de loop van die week zichtbaar is.