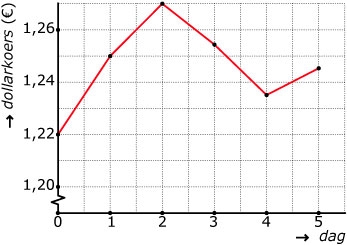
Veranderingen per stap

Antwoorden bij de opgaven

1. t	0	3	6	9	12	15	18	21	24
   T	10	7,5	8	12	17	21	18	13	8
   ΔT	--	–2,5	0,5	4	5	4	–3	–5	–5

2. 

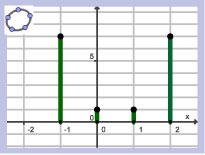
   x	–2	–1	0	1	2
   y	–8	–1	0	1	8
   Δy	--	7	1	1	7

3. 1. GR: Y1=X^3+^*X en Y2=Y1(X)–Y1(X–1) en tabel met stapgrootte 1.
   2. D
   3. -
4. 

5. 1. x	0	1	2	3	4	5	6	7	8	9	10	11	12
      y	4	5	7	10	7	5	4	3	2	1	0	–1	–2

   2. B

6. x	–2	–1	0	1	2	3
   y	–4	–1	4	5	4	1
   Δy	--	5	3	1	–1	–3

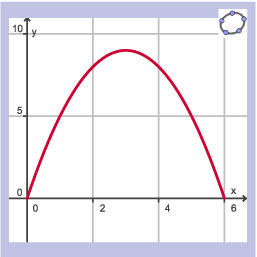
7. 1. GR: Y1=0.5X^4–4X^2+8 en Y2=Y1(X)–Y1(X–1); tabel met stapgrootte 0,5 vanaf `x=-3`.
   2. `(:0,1:)`
   3. Drie keer tekenwisseling bij de toenames.
8. 1. 
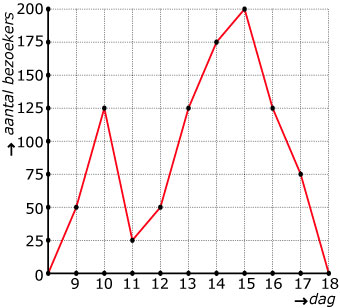
   2. Rond 15:00 uur
   3. Nee, niet precies, er is maar om het uur gemeten.
9. 1. Tabel maken van `V`
   2. 
   3. 
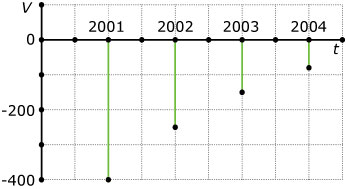
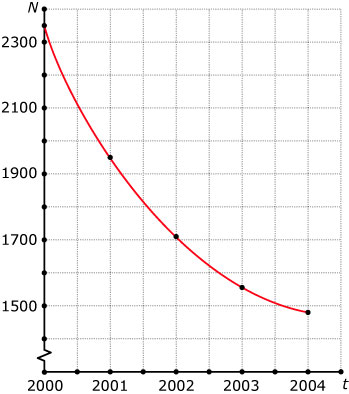
   4. Afnemende daling, de afnames worden kleiner.
   5. De afnames naderen naar 0. De grafiek van `N` heeft dan een horizontale asymptoot.
10. 1. 
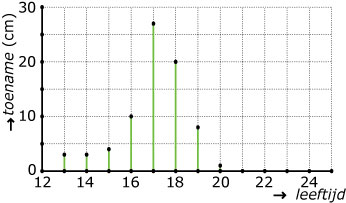
    2. Alle toenames zijn positief of 0.
    3. Er is om het jaar gemeten, wat er binnen zo'n jaar gebeurt weet je niet. Hoewel een dalende lichaamslengte voor iemand's 25e wel wat vreemd zou zijn...
    4. Ongeveer vanaf zijn 20e verjaardag. De toenames zijn dan vrijwel 0.
    5. Vanaf zijn 12e tot zijn 15e verjaardag. De toenames zijn dan constant.
11. 1. GR: Y1=-0.5X^4+4X^2 en Y2=Y1(X)–Y1(X–1); tabel met stapgrootte 0,5 vanaf `x=-4`
    2. `(:-1,0:)`, de afnames worden dan kleiner
    3. Waar tekenwisseling plaats vindt.
12.