Veeltermen

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Machtsfuncties > Veeltermen > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Machtsfuncties > Veeltermen > Uitleg

Lees eerst de Uitleg goed door.

Opgaven

  1. Bekijk de Uitleg.
    1. Bepaal met de grafische rekenmachine beide toppen van de grafiek in twee decimalen nauwkeurig.
    2. Bereken de exacte snijpunten van de grafiek van `f` met de parabool `y = -4x^2`.

  2. Neem de kwadratische functie `g` met `g(x) = 0,5x^4 - 8x^2`.
    1. Bereken algebraïsch de drie nulpunten van deze functie.
    2. Bereken de toppen van de grafiek van `g` met de grafische rekenmachine. (`x`-waarden in twee decimalen nauwkeurig.)
    3. Los op `f(x) < 4 - x^2`.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Machtsfuncties > Veeltermen > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

  1. Gebruik de applet in de Theorie. Derdegraads functies hebben de vorm `f(x) = bx^3 + cx^2 + dx + e` met `b != 0`.
    1. Neem `b=1, c=0, d=0` en `e=0`. Hoeveel nulpunten heeft `f` dan? En hoeveel toppen?
    2. Neem `b=1, c=4, d=0` en `e=0`. Hoeveel nulpunten heeft `f` dan? En hoeveel toppen?
    3. Neem `b=1, c=0, d=4` en `e=0`. Hoeveel nulpunten heeft `f` dan? En hoeveel toppen?
    4. Neem `b=1, c=0, d=-4` en `e=0`. Hoeveel nulpunten heeft `f` dan? En hoeveel toppen?
    5. Hoeveel nulpunten en hoeveel toppen heeft een derdegraads functie maximaal?

  2. Bekijk de vierdegraads functie `f(x) = 2x^4 - 512x^2`. Je wilt de nulpunten en de toppen van de grafiek van `f` bepalen. Bekijk Voorbeeld 1.
    1. Bereken de exacte nulpunten van `f`.
    2. Bij welke vensterinstellingen krijg je nu de grafiek van `f` goed in beeld?
    3. Hoeveel toppen zijn er? Bepaal de extremen van `f` in één decimaal nauwkeurig.

  3. Je wilt de ongelijkheid `0,5x^4 - 60x^2 < x^2 - 200` oplossen. Bekijk eventueel Voorbeeld 2.
    1. Eerst breng je de grafieken goed in beeld. Bereken daartoe de nulpunten van `y_1 = 0,5x^4 - 60x^2` en die van `y_2 = x^2 - 200`.
    2. Los `y_1 = y_2` op met de grafische rekenmachine en geef de oplossing van de ongelijkheid in één decimaal nauwkeurig.

  4. In Voorbeeld 3 zie je een praktijkvoorbeeld waarin een derdegraads functie voorkomt.
    1. Breng zelf de grafiek in beeld.
    2. Licht de mogelijke antwoorden op de vraag met behulp van de grafiek en de bijpassende tabel toe.

Verwerken

  1. Gegeven de functie `f` met `f(x) = (x^2 - 4)^2 - 100`.
    1. Laat zien dat hier sprake is van een vierdegraads functie.
    2. Bereken algebraïsch de nulpunten van de grafiek van `f`.
    3. Bereken de extremen van `f`.
    4. Los algebraïsch op: `f(x) <= -91`.

  2. Los de volgende vergelijkingen en ongelijkheden algebraïsch op:
    1. `x^3 - 4x^2 = 21x`
    2. `x(x^3 - 1) <= 7x`
    3. `x(6 - x)(x + 5) >= 0`
    4. `2x^4 - 12x = -18x`
    5. `x^4 - 7x^3 + 10x^2 = 0`
    6. `60 - 0,5x^4 >= 0`

  3. ChemTech produceert een bepaald onkruidbestrijdingsmiddel. Voor de productiekosten per maand gelden deze gegevens:

    `q` (in duizenden kg per maand)123456
    `TK` (in euro per maand)77510001220200040008000

    Hierin is `q` de geproduceerde hoeveelheid per maand in duizenden kg en is `TK` de totale kosten in euro. Verder verkoopt ChemTech dit middel voor € 2,25 per kg.
    1. De bedrijfsleiding heeft voor de kostenfunctie deze formule bedacht `TK = 100q^3 - 600q^2 + 1300q`. Laat zien dat deze formule redelijk goed bij de gegeven tabel past.
    2. Stel een formule op voor de totale winst `TW` afhankelijk van `q`. Ga er van uit dat de geproduceerde hoeveelheid elke maand ook wordt verkocht.
    3. Bepaal met de grafische rekenmachine bij welke productie per maand de winst maximaal is.

Testen

  1. Los de volgende vergelijkingen en ongelijkheden algebraïsch op.
    1. `x^4 - 8x >= 0`
    2. `-x^2(x - 5) = 2x^2`
    3. `20 - x^4 = 11`
    4. `(x^2 - 4)(x^2 - 9) < 36`

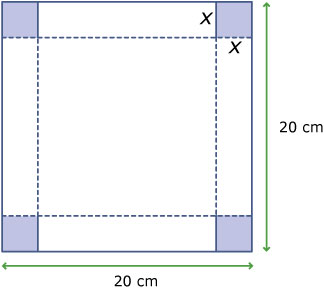  2. Je maakt een bakje met een open bovenkant door van een vierkant stuk karton van 20 cm bij 20 cm de vier hoeken in te knippen en als plakstroken te gebruiken. De ingeknipte hoeken zijn vierkantjes van `x` cm bij `x cm`.
    Er ontstaan zo een bakje met een hoogte van `x` cm.
    1. Welke afmetingen heeft de bodem van het bakje nu?
    2. Stel een formule op voor de inhoud `I(x)` van dit bakje.
      (Hoewel de bovenkant open is moet je er van uit gaan van er niets boven het bovenvlak uitsteekt!)
    3. Voor welke waarden van `x` is de inhoud van het bakje groter dan 500 cm3?