De abc-formule

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Machtsfuncties > De abc-formule > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Machtsfuncties > De abc-formule > Uitleg

Lees eerst de Uitleg goed door. Bekijk vooral hoe de `abc`-formule werkt.

Opgaven

1. Gegeven is de kwadratische functie `f` met functievoorschrift `f(x) = x^2 + 6x + 1`. Je wilt de nulpunten van `f` berekenen.
   1. In de Uitleg, pagina 1 kun je zien hoe dat in zijn werk gaat. Leg uit waarom `x^2 + 6x = (x + 3)^2 - 9`.
   2. Bereken algebraïsch de nulpunten van de grafiek van `f` in twee decimalen nauwkeurig.
   3. Je kunt deze nulpunten ook vinden met de `abc`-formule, zie de Uitleg, pagina 2. Bepaal de nulpunten nog eens, maar nu met de `abc`-formule.
   4. Welke top heeft de grafiek van `f`?


2. Neem de kwadratische functie `g` met `g(x) = x^2 + 8x + 3`. Je wilt weer de nulpunten berekenen.
   1. Laat zien dat `g(x) = (x + 4)^2 - 13`.
   2. Bepaal nu exact de beide nulpunten.
   3. Welke top heeft de grafiek van `g`?
   4. Bepaal beide nulpunten ook met behulp van de `abc`-formule. Laat zien dat je dezelfde nulpunten vindt dan bij b.
   5. Wat is het nadeel van het gebruik van de `abc`-formule?


3. De vergelijking `2x^2 + 8x = 24` kun je op meerdere manieren oplossen.
   1. Los deze vergelijking op door ontbinden in factoren.
   2. Je kunt deze vergelijking ook oplossen door hem te schrijven als `(x - 2)^2 = 16`. Laat zien hoe dat gaat en los hem dan verder op.
   3. Tenslotte kun je deze vergelijking oplossen met de `abc`-formule. Doe dat ook nog een keer.
   4. Welke methode vind je het handigst en waarom?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Machtsfuncties > De abc-formule > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

4. Bestudeer Voorbeeld 1. Je gaat nu zelf de vergelijking `x^2 + 12x = 30` oplossen.
   1. Doe dit eerst door de vergelijking te schrijven als `(x + 6)^2 = 66`.
   2. Doe dit vervolgens nog eens met de `abc`-formule.


5. Bekijk de kwadratische functie `f(x) = 2x^2 - 6x + 2`. Je wilt de nulpunten (in twee decimalen nauwkeurig) en de top van de grafiek van `f` bepalen. Bekijk Voorbeeld 2.
   1. Probeer dit eerst met behulp van kwadraat afsplitsen.
   2. Je kunt de nulpunten ook meteen met de `abc`-formule berekenen. Bepaal wat dan de `a`, `b` en `c` zijn. Bereken daarna de discriminant.
   3. Kun je aan de discriminant zien hoeveel oplossingen de vergelijking `f(x)=0` heeft?
   4. Los de vergelijking `f(x)=0` op en ga na dat je zo dezelfde nulpunten vindt als bij a.
   5. Werk je met de `abc`-formule, dan moet je vanuit de nulpunten de top bepalen. Hoe gaat dat in zijn werk?


6. Je wilt de ongelijkheid `3x^2 + 6x < x + 8` oplossen. Als je de `abc`-formule wilt gebruiken om een vergelijking op te lossen, moet de vergelijking in de vorm `ax^2 + bx + c = 0` staan. Bekijk Voorbeeld 3.
   1. Schrijf de bij de ongelijkheid horende vergelijking `3x^2 + 6x = x + 8` in deze vorm en bereken de oplossingen met de `abc`-formule.
   2. Controleer de oplossingen met de grafische rekenmachine en geef de oplossing van de ongelijkheid.


7. Kwadratische vergelijkingen kunnen soms ook opgelost worden door ontbinden in factoren. Ga bij elk van de volgende vergelijkingen na of ze opgelost kunnen worden met ontbinden in factoren. Bereken van elk van de vergelijkingen de oplossing. Gebruik de `abc`-formule alleen als dat echt nodig is.
   1. `x^2 - x - 3 = 0`
   2. `-4x^2 + 5x - 14=0`
   3. `2x^2 - 10x + 10 = 2x - 6`
   4. `x - 5x^2 = 10`
   5. `x(x - 7) = 8`

Verwerken

8. Gegeven de kwadratische functie `f` met `f(x) = x^2 + 8x - 20`.
   1. Schrijf het functievoorschrift in een zodanige vorm dat je de top van de grafiek eruit kunt aflezen.
   2. Je kunt nu op drie manieren de nulpunten van de grafiek van `f` berekenen. Doe dit eerst door het functievoorschrift dat je bij a hebt gevonden te gebruiken
   3. Bereken de nulpunten ook met behulp van de `abc`-formule.
   4. Tenslotte kun je gebruik maken van ontbinden in factoren. Dat gaat verreweg het snelst als je de ontbinding "ziet". Bereken de nulpunten nog eens op deze manier.


9. Teken met de grafische rekenmachine en één figuur de grafieken van `f(x) = 2x^2 - x + 1` en `g(x) = 10 - 3x`.
   1. Los op: `f(x) = g(x)`
   2. Los in drie decimalen nauwkeurig op: `f(x) > g(x)`


10. Los de volgende vergelijkingen op:
    1. `x^2 + 3x + 13 = 0`
    2. `1/3x^2 + 10x + 1 = 0`
    3. `2x^2 - 5x = x`
    4. `2x^2 - 12x = -18`
    5. `x^2 - 5x + 10 = 0`
    6. `x(x - 1) = 12`
    7. `60 - x^2 = 0`
    8. `5 - 1/3x^2 = 1`
    9. `x - 5x^2 = 3`

Testen

11. Los de volgende vergelijkingen en ongelijkheden algebraïsch op.
    1. `x^2 - 2x - 15 = 0`
    2. `-x^2 - x - 1 = 0`
    3. `20 - x^2 = 11`
    4. `x(x + 2) < 14`
    5. `x^2 - x + 10 >= 3`


12. Gegeven zijn de functies `f(x) = 100 - x^2` en `g(x) = 1/2 x^2 - 10x`.
    1. Bereken de nulpunten van de grafieken van `f` en `g`.
    2. Bereken algebraïsche de snijpunten van de twee grafieken van `f` en `g` in twee decimalen nauwkeurig.


13. Een basketballer maakt een driepunter zonder het bord te raken (hij gooit de bal dus in één keer door de ring van de basket). De baan van de bal is (ongeveer) een parabool, zie figuur. Het hoogste punt van de baan is gegeven. De speler laat de bal op 2,5 m boven de grond los.
    
    
    
    
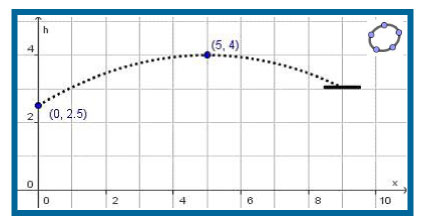
    1. Stel een formule op voor de functie `h(x)` die de baan van de bal beschrijft.
    2. De ring van de basket hangt op 3,05 m boven de grond. Hoe ver staat de speler vanaf (het midden van) de ring van de basket?