
Totaalbeeld
Samenvatten
Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Functies en grafieken. Een eigen samenvatting maken is nuttig.
Begrippenlijst:
21: functie invoerwaarde functiewaarde functievoorschrift
22: domein bereik nulwaarden/nulpunten extremen/toppen
23: lineaire functie kwadratische functie familie van functies, parameters
24: asymptoten karakteristieken (nulpunten, toppen, asymptoten)
25: ongelijkheid
Activiteitenlijst:
21: functies herkennen de notaties bij het functiebegrip gebruiken
22: het domein en het bereik van een functie bepalen de intervalnotatie gebruiken
23: werken met lineaire functies en kwadratische functies
24: asymptoten bepalen karakteristieken van een functie bepalen
25: ongelijkheden oplossen
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Achtergronden
Testen
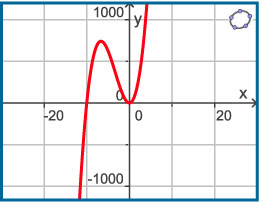 Gegeven zijn de functies `f(x) = 5x^2(x + 20)` en `g(x) = 50x^2`.
De grafiek van `f` zie je hiernaast.
Gegeven zijn de functies `f(x) = 5x^2(x + 20)` en `g(x) = 50x^2`.
De grafiek van `f` zie je hiernaast.
-
Bereken algebraïsch de nulpunten van `f` en breng de grafiek in beeld.
Pas de vensterinstellingen zo aan, dat je hetzelfde beeld krijgt als in de gegeven grafiek.
Zet nu ook de grafiek van `g` er bij.
-
Bereken de snijpunten van de grafieken van `f` en `g`.
-
Los op: `f(x) < g(x)`.
-
Bereken bij deze functies eerst de nulpunten. Bepaal vervolgens domein en bereik.
-
`f(x) = x^2(x^2 - 400)`
-
`g(x) = sqrt(20-x) - 40`
-
Gegeven is de functie `y(x) = 4 - 1/(x^2)`.
-
Welke asymptoten heeft de grafiek van deze functie?
-
Schrijf domein en bereik op.
-
Los op: `y >= 2`. Geef benaderingen in twee decimalen nauwkeurig.
-
Een sneeuwbal wordt van een hele lange besneeuwde helling gerold. De sneeuwbal
wordt daardoor bij elke omwenteling dikker.
Stel je eens voor dat die sneeuwbal op het moment van loslaten een diameter van
10 cm heeft en zuiver rond is. Neem aan dat de sneeuwbal telkens zuiver rond
blijft en dat bij elke omwenteling de diameter met 1 cm toeneemt. Het volume
V van een zon bol kun je berekenen met de formule
`V =4/3pi * r^3`
waarin `r` de straal van de bol is.
De hoeveelheid sneeuw `S` waaruit de sneeuwbal bestaat is een functie van het
aantal omwentelingen `a`.
-
Stel een functievoorschrift voor `S(a)` op.
-
Breng de grafiek in beeld.
Schrijf op bij welke vensterinstellingen een bij de situatie passend deel van de grafiek in beeld komt.
-
Na hoeveel onderwentelingen heeft de sneeuwbal een volume van ongeveer 1000 dm3?
-
Gegeven is de functie `f` met `f(x) = 0,25(x - 10)^4 - 16`.
-
Bereken de nulpunten van de grafiek van `f`. Welk minimum heeft de grafiek van `f`?
-
Los algebraïsch op: `f(x) < 10`.
-
Als je een gewicht vrij aan een touw laat slingeren, dan geldt:
`T = 2pi * sqrt(l/(9,8))`
waarbij `T` de slingertijd in seconden en `l` de lengte van het touw in m is. De
slingertijd is de tijd waarin de slinger precies één keer heen en weer beweegt.
-
Als `0 <= l <= 4`, welke waarden kan `T` dan aannemen?
-
Als de slingertijd 3 s is, hoe lang is dan het touw?
Bepaal het antwoord zowel door terugrekenen als met je grafische rekenmachine in twee decimalen nauwkeurig.
-
Waarom is de lengte van het touw ook een functie van `T`? Stel het functievoorschrift op voor `l(T)`.
Toepassen
-
Door een technische storing in de airconditioning van een groot gebouw neemt het zuurstofgehalte in de lucht tijdelijk af. Lees hierover meer in...
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Toepassingen
De technische staf heeft het verloop van het zuurstofgehalte beschreven met de formule:
`Z(t) = 200(1 - (10)/(t+10) + (100)/((t+10)^2))`
Hierin is `t` de tijd in minuten gerekend vanaf het moment dat de storing begon. Verder is `Z` het aantal cm3 zuurstof per liter lucht op het tijdstip `t`. Op `t = 0` is het zuurstofgehalte normaal.
-
Bereken `Z(0)`. Schets de grafiek van `Z(t)` voor `0 <= t <= 100`.
-
Op welk tijdstip is het zuurstofgehalte minimaal?
-
De medische staf vindt een zuurstofgehalte van 80% van het normale niveau, nog juist toelaatbaar.
Bereken gedurende hoeveel minuten het zuurstofgehalte ontoelaatbaar laag is.
-
Bestudeer het economische model in...
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Toepassingen
Er wordt een formule afgeleid voor de winst die een bedrijf per week maakt bij de verkoop van een bepaald artikel.
-
Leid zelf deze formule af.
-
Bereken de maximale winst die dit bedrijf per week kan maken.
Een levensmiddelenbedrijf heeft 30000 blikken bonen ingekocht voor € 0,90 per stuk.
Men wil die blikken bonen binnen 30 werkdagen als aanbieding verkopen.
Uit ervaring weet de handelaar dat zijn prijs bepaalt hoeveel blikken bonen hij per dag kan verkopen en dat hij daarvoor uit kan gaan van de volgende formule: `p=2,5-q/1000` waarin `p` de verkoopprijs in € per blik is en `q` het aantal blikken dat hij per dag verkoopt.
-
Als hij deze blikken bonen verkoopt voor € 1,60 per stuk, raakt hij ze dan binnen de gestelde termijn kwijt?
En maakt hij winst op de partij?
-
Bij welke verkoopprijs per blik is zijn winst maximaal als hij de termijn van 30 werkdagen om alles te verkopen laat vallen?
-
Van een rechthoekig stuk karton van 12 cm bij 20 cm kun je een bakje maken. Je knipt dan de vier hoeken even ver in, zoals je in de figuren kunt zien.
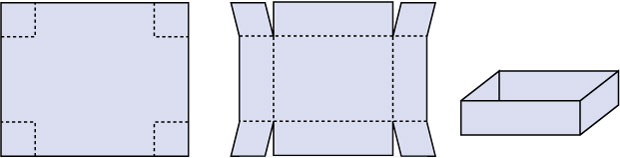
Als je er op dezelfde wijze een deksel bij maakt, krijg je een doosje waarvan de inhoud `I` wordt bepaald door de afmetingen van het bakje.
-
Noem de lengte en de breedte van het ingeknipte stukje `x`. Stel een formule op voor `I(x)`.
-
Bepaal het domein en het bereik van `I(x)`.
-
Hoe ver moet je het karton inknippen om een maximale inhoud te krijgen?
Examenopgaven
-
Toltunnel
Het aantal personenauto's (`A`) dat per dag van een nieuw aan te leggen toltunnel gebruik zal maken, is volgens een verkeersdeskundige te berekenen met de formule:
`A = 400T^2 - 9150T +46800`
Hierbij is `T` het toltarief in euro. Toltarieven hoger dan € 7,- blijven buiten beschouwing.
Met het oog op een snelle doorstroming zal de betaling op elektronische wijze geschieden.
Hierdoor is het mogelijk om een toltarief van € 2,67 in rekening te brengen omdat dat niet op praktische bezwaren stuit.
-
Bereken de totale dagopbrengst aan tolgeld voor personenauto's bij een toltarief van € 2,-.
-
Bereken in centen nauwkeurig bij welk toltarief de totale dagopbrengst aan tolgeld voor personenauto's maximaal is.
-
Bereken met hoeveel procent het aantal personenauto's afneemt als bij een tarief van € 2,40 een tariefsverhoging van 2% wordt toegepast.
(bron: examen wiskunde A vwo 1992, eerste tijdvak; gulden vervangen door euro)
Wielrennen
Bij wielrennen gaat het er meestal om in een zo kort mogelijke tijd een gegeven afstand
af te leggen. Daarnaast kent men het wereld-uurrecord. Daarbij gaat het erom in
precies één uur een zo groot mogelijke afstand af te leggen.
Op 2 september 1994 reed Miguel Indurain op de wielerbaan van Bordeaux in één uur
53,040 km. Hij vestigde daarmee het wereld-uurrecord. Kort daarna raakte hij zijn
record kwijt aan Toni Rominger, die op 5 november 1994 op dezelfde baan in één uur
55,291 km reed.
De afgelegde afstand bestaat uit een groot aantal rondes op de wielerbaan. Elke ronde
is 250 meter.
Stel dat Indurain en Rominger deze ritten tegelijkertijd hadden gereden, en naast
elkaar waren gestart en dat ieder met constante snelheid reed.
-
Hoeveel keer zou Rominger na de start in de loop van het uur Indurain hebben ingehaald?
Licht je antwoord toe.
Om te voorspellen of een wielrenner een bepaalde snelheid kan halen, kijkt men naar
het daarvoor benodigde vermogen (`W`), dat is de energie die de wielrenner per seconde
moet leveren. Daarbij speelt de luchtweerstand een belangrijke rol. De luchtweerstand
kan onder andere verkleind worden door de stroomlijn van fietser en fiets te
verbeteren.
Men gebruikt vaak de volgende formule voor `W`:
`W = ( k * v^2 + 4 ) * v`
Hierbij geldt:
- `v` is de snelheid (in m/sec);
- `W` is het vermogen (in joule/sec) dat de wielrenner moet leveren;
- `k` is een getal dat onder andere te maken heeft met de luchtweerstand.
Daan wil zich op de wielersport gaan toeleggen.Van een medische keuring weet hij dat
hij gedurende enige tijd een vermogen kan leveren van 190 joule/sec. Op zijn huidige
fiets haalt hij een snelheid van 33 km/uur, dus ruim 9 m/sec. Met behulp van
bovenstaande formule leidt hij hieruit af dat `k = 0,2`.
Door veel te trainen hoopt Daan een vermogen te kunnen leveren van 300 joule/sec.
Om er achter te komen wat de maximale snelheid is die hij dan kan halen, tekent hij
voor `k = 0,2` de grafiek van W als functie van v. Hij kan nu aflezen dat zijn
maximale snelheid dan bijna 11 m/sec zal zijn (ongeveer 39 km/uur).
Daan is ook van plan een nieuwe fiets en nieuwe fietskleding te kopen.Volgens kenners
kan hij daarmee `k` verlagen tot `k = 0,15`. Daan vraagt zich af welke snelheid hij dan kan
behalen. Om de vraag te kunnen beantwoorden, moet hij een nieuwe grafiek tekenen.
-
Welke snelheid (in km/uur) zal Daan kunnen behalen met een vermogen van 300 joule/sec, bij k = 0,15?
Licht je antwoord toe met behulp van een grafiek.
 De wielerbaan van Bordeaux ligt op zeeniveau.
Voordat Indurain en Rominger hun eerder genoemde recordritten reden, beweerde
iemand dat de magische grens van 55 kilometer in één uur slechts op grote hoogte
boven zeeniveau bereikt zou kunnen worden. (Daar is de lucht ijler en dus de
luchtweerstand kleiner. Daardoor is `k` kleiner.)
De wielerbaan van Bordeaux ligt op zeeniveau.
Voordat Indurain en Rominger hun eerder genoemde recordritten reden, beweerde
iemand dat de magische grens van 55 kilometer in één uur slechts op grote hoogte
boven zeeniveau bereikt zou kunnen worden. (Daar is de lucht ijler en dus de
luchtweerstand kleiner. Daardoor is `k` kleiner.)
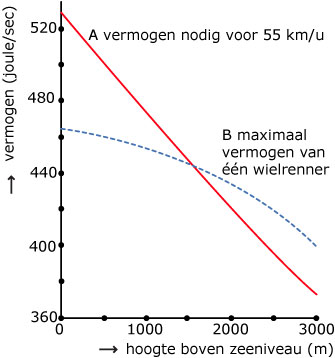
Om zijn bewering te illustreren maakte hij deze figuur. Hierin is grafiek A als volgt tot
stand gekomen.
Bij een officieel record moeten fiets en berijder aan allerlei voorschriften voldoen. De
mogelijkheden om binnen deze voorschriften de stroomlijn te verbeteren leken optimaal
benut. Daarmee lag voor elke hoogte de waarde van `k` vast. Met behulp van de
formule voor `W` kon hij dus berekenen hoeveel vermogen een wielrenner nodig had
om 55 km/uur (15,3 m/sec) te fietsen.
Zo is bijvoorbeeld, volgens de maker van deze figuur, op zeeniveau `k = 0,13`.
-
Bereken hoe groot `k` is op 2000 meter hoogte volgens de maker van de figuur.
In grafiek B van de figuur is het maximale vermogen te zien dat een ideale wielrenner
een uur lang zou kunnen leveren. (Ook dat neemt af naarmate men hoger komt,
doordat de ijlere lucht minder zuurstof bevat.)
Volgens de maker van de figuur zou de prestatie van Rominger (55,291 km) op
zeeniveau onmogelijk zijn. Het record van Indurain was 53,040 km.
-
Onderzoek met behulp van de formule voor `W` of het record van Indurain volgens de maker van de figuur op zeeniveau wel mogelijk is.
(bron: examen wiskunde A vwo 1999, tweede tijdvak)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Achtergronden  Gegeven zijn de functies `f(x) = 5x^2(x + 20)` en `g(x) = 50x^2`.
De grafiek van `f` zie je hiernaast.
Gegeven zijn de functies `f(x) = 5x^2(x + 20)` en `g(x) = 50x^2`.
De grafiek van `f` zie je hiernaast.
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Toepassingen
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Totaalbeeld > Toepassingen

 De wielerbaan van Bordeaux ligt op zeeniveau.
Voordat Indurain en Rominger hun eerder genoemde recordritten reden, beweerde
iemand dat de magische grens van 55 kilometer in één uur slechts op grote hoogte
boven zeeniveau bereikt zou kunnen worden. (Daar is de lucht ijler en dus de
luchtweerstand kleiner. Daardoor is `k` kleiner.)
De wielerbaan van Bordeaux ligt op zeeniveau.
Voordat Indurain en Rominger hun eerder genoemde recordritten reden, beweerde
iemand dat de magische grens van 55 kilometer in één uur slechts op grote hoogte
boven zeeniveau bereikt zou kunnen worden. (Daar is de lucht ijler en dus de
luchtweerstand kleiner. Daardoor is `k` kleiner.)