
Bijzondere functies
Inleiding
Je kent al diverse functies. Alleen sprak je tot nu toe vaak over verbanden en formules. Denk nog even terug aan de lineaire verbanden, de kwadratische verbanden en de hyperbolische verbanden. Het gaat daarbij eigenlijk steeds over functies.
In dit onderdeel komen enkele bijzondere functies voorbij.
Je leert nu:
- werken met lineaire functies;
- werken met kwadratische functies.
Je kunt al:
- het begrip functie en de bijbehorende notaties gebruiken;
- het domein en het bereik van een functie vinden;
- de intervalnotatie gebruiken.
Verkennen
Je staat op een viaduct over de snelweg A1.
Je ziet een auto rijden met een snelheid van 90 km/h.
Precies 6 minuten later zie je een tweede auto onder het viaduct uitkomen.
Deze tweede auto rijdt 120 km/h en in dezelfde richting als de eerste auto.
> Teken bij elk van deze auto’s de grafiek van de afstand tot het viaduct.
Zet beide grafieken in één figuur en kies geschikte eenheden.
> Na hoeveel minuten heeft de tweede auto de eerste ingehaald?
(Gebruik je grafieken of geef een berekening.)
Uitleg
Twee auto’s rijden met een constante snelheid over dezelfde weg.
Auto 1 gaat van A naar B met een constante snelheid van 90 km/h en auto 2 van B naar A met een constante snelheid van 120 km/h.
A en B liggen 50 km van elkaar verwijderd. Beide auto’s zijn op hetzelfde moment
gestart. Als je wilt berekenen op welk tijdstip ze elkaar tegenkomen, stel je (bijvoorbeeld)
de afstand tot A voor door de variabele a. Neem voor de tijd in minuten de variabele t.
Omdat auto 1 met 1,5 km per minuut rijdt, geldt: a1 = 1,5t.
Voor auto 2 geldt a2(0) = 50 en dus: a2 = 50 – 2t.
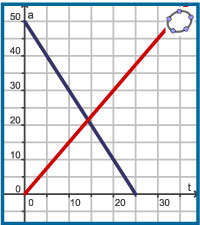
Bij beide formules is er een lineair verband tussen a en t:
a1 en a2 zijn lineaire functies. Je ziet hier de beide grafieken, het zijn rechte lijnen.
De auto’s komen elkaar tegen als 1,5t = 50 – 2t.
Als je deze vergelijking oplost vind je t ≈ 14,3 minuten.
Vaak kun je de afgelegde weg van een auto goed berekenen door aan te nemen dat hij voortdurend met dezelfde (gemiddelde) snelheid heeft gereden. Maar als een auto optrekt neemt zijn snelheid voortdurend toe. De afgelegde weg neemt dan niet lineair toe, maar kwadratisch.
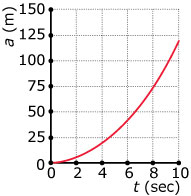
Hier zie je de grafiek van een vanuit stilstand optrekkende auto, waarbij a de afgelegde weg (in meter) en t de tijd (in seconden) is.
Ga na, dat a(t) = 1,2t2.
Na 5 seconden heeft de auto 30 m afgelegd.
De gemiddelde snelheid is 6 m/s, dus ongeveer 22 km/h.
Na 10 seconden heeft de auto 120 m afgelegd.
De gemiddelde snelheid is 12 m/s, dus ongeveer 44 km/h.
Je ziet dat de snelheid toeneemt...
‡
Opgaven
-
Bekijk de eerste pagina van de Uitleg.
Twee auto’s rijden met een constante snelheid over dezelfde weg. Auto 1 gaat van `A` naar `B` met een constante snelheid van 90 km/h en auto 2 van `B` naar `A` met een constante snelheid van 120 km/h.
-
In de Uitleg wordt de afstand van beide auto’s tot `A` bekeken.
Bekijk die afstand nu vanuit `B`. Schrijf de twee bijpassende formules op.
- Onderzoek door berekening of beide auto’s elkaar nu op hetzelfde tijdstip tegenkomen.
-
Voor welke twee waarden van `t` bedraagt de onderlinge afstand van beide auto's 20 km?
-
Ga nu naar de tweede pagina van de Uitleg.
Daar zie je een mogelijke grafiek van een optrekkende auto.
-
Hoe zie je aan de grafiek dat de snelheid steeds toeneemt?
-
Met het schakelen naar een hogere versnelling is in de grafiek geen rekening gehouden. Hoe zie je dat?
-
Na hoeveel seconden is de gemiddelde snelheid ongeveer 60 km/h? (Ga er dus van uit dat er niet hoeft te worden geschakeld.)
Theorie
Er bestaan veel verschillende soorten functies.
Als y een lineaire functie is van x heeft het functievoorschrift de vorm y = ax + b, waarin
- a het hellingsgetal is;
- b het begingetal, de functiewaarde bij x = 0 is.
De grafiek van een lineaire functie is een rechte lijn door (0, b) en (1, b + a).
Voor "hellingsgetal" wordt wel het woord richtingscoëfficiënt gebruikt, want dit getal bepaalt de richting van de grafiek.
Als y een kwadratische functie is van x heeft het functievoorschrift de vorm y = ax2 + bx + c of is het in die vorm te schrijven.
De vorm van de grafiek hangt af van de waarden van a, b en c, maar is altijd een parabool.
Bij het berekenen van nulpunten maak je vooralsnog gebruik van ontbinden in factoren.
‡
Voorbeeld 1
Als een fabrikant als enige een bepaald product verkoopt, gaan economen uit van een lineair verband tussen het aantal q exemplaren dat hij verkoopt en de prijs p die hij vraagt. q is dan een lineaire functie van p.
Een voorbeeld daarvan is een functie met voorschrift q = 4000 – 200p.
Welke prijzen kan de fabrikant volgens dit model vragen? En welke aantallen kan hij verkopen?
Antwoord
Zowel p als q moeten positieve waarden hebben.
Neem je p = 0, dan is q = 4000.
Neem je q = 0, dan is p = 20. (Vergelijking oplossen.)
Dit betekent dat p van 0 tot 20 kan lopen en q van 4000 tot 0.
Handig om van tevoren te bedenken als je de grafiek op je grafische rekenmachine in beeld wilt brengen.
‡
Voorbeeld 2
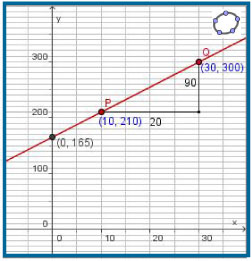 Je ziet hier de punten P(10,210) en Q(30,300).
Je ziet hier de punten P(10,210) en Q(30,300).
Stel een functievoorschrift op voor de functie waarvan de grafiek een rechte lijn door `P` en `Q` is.
Antwoord
Er is sprake van een lineaire functie f.
Je zoekt daarom het hellingsgetal en het begingetal (de functiewaarde bij 0).
Vergelijk de twee gegeven punten van de grafiek.
Bij een toename van x met 30 – 10 = 20
hoort een toename van y met 300 – 210 = 90.
Dus bij een toename van x met 1 hoort een toename van y met `90/20=4,5`.
Daarom is het hellingsgetal 4,5.
De functiewaarde bij 0 is niet bekend.
De functie heeft een voorschrift van de vorm f(x) = 4,5x + b.
Omdat f(10) = 210 geldt: 210 = 4,5 ·10 + b.
En dit geeft b = 165.
Dus het functievoorschrift is f(x) = 4,5x + 165.
‡
Voorbeeld 3
In bepaalde economische omstandigheden (zie voorbeeld 1) hangt het aantal exemplaren q dat een fabrikant verkoopt af van de prijs p volgens een lineaire functie: q = 4000 – 200p.
De totale opbrengst TO bereken je dan zo: TO = p · q = p · (4000 – 200p).
TO is dus een kwadratische functie van p.
Bij welke prijs is de opbrengst maximaal?
Antwoord
De nulwaarden van TO bereken je uit: p · (4000 – 200p) = 0.
Dat levert op: p = 0 V p = 20.
De grafiek van TO is een parabool door (0,0) en (20,0) en heeft dus zijn maximum bij p = 10. (Een parabool is immers symmetrisch?)
Als de maximale opbrengst zelf ook wordt gevraagd, vul je nog even p = 10 in de functie TO(p) in.
‡
Opgaven
-
Bekijk de Theorie.
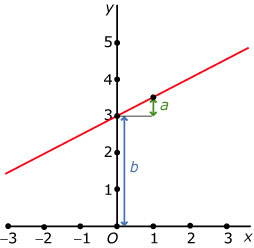
Elke lineaire functie `f` heeft een functievoorschrift van de vorm `f(x) = ax + b`.
In de figuur hebben `a` en `b` vaste waarden.
-
Welke betekenis heeft de `a` voor de grafiek van `f`?
-
Welke betekenis heeft de `b` voor de grafiek van `f`?
-
Welke waarden voor `a` en `b` moet je instellen om als grafiek de rechte lijn door `A(0,3)` en `B(1;3,5)` te krijgen?
-
Hoe kun je het bijbehorende functievoorschrift afleiden uit de coördinaten van `A` en `B`?
-
Ga nu naar Voorbeeld 1. Daar wordt een economisch model beschreven.
-
Heeft de gegeven formule inderdaad de vorm van een lineaire functie?
Wat is dan de richtingscoëfficiënt?
-
Maak een grafiek bij `q=4000-200p`. Welke vensterinstellingen gebruik je?
-
Bij welke prijs verkoopt hij 1500 exemplaren?
-
Voor een rit in een taxi betaal je voorrijkosten en een bedrag per gereden kilometer:
- voorrijkosten € 3,20
- per gereden km € 1,20
De ritprijs (`R`) hangt af van het aantal gereden kilometer (`a`).
-
Laat zien dat `R(10) = 15,2`.
-
Stel een voorschrift op voor de functie `R(a)`.
-
Dit is een voorbeeld van een lineaire functie. Teken de grafiek van deze functie op je grafische rekenmachine.
-
Waar vind je de twee getallen 3,20 en 1,20 in je grafiek terug?
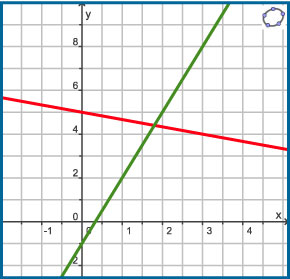 Bekijk in Voorbeeld 2 hoe je het voorschrift opstelt van een lineaire functie als twee punten van de grafiek zijn gegeven.
Je ziet hier twee grafieken van lineaire functies. Stel voor elk van deze functies een passend voorschrift op en bereken algebraïsch het snijpunt van beide lijnen.
Bekijk in Voorbeeld 2 hoe je het voorschrift opstelt van een lineaire functie als twee punten van de grafiek zijn gegeven.
Je ziet hier twee grafieken van lineaire functies. Stel voor elk van deze functies een passend voorschrift op en bereken algebraïsch het snijpunt van beide lijnen.
-
Voorbeeld 3 gaat over een kwadratische functie.
-
Laat door het uitwerken van de haakjes zien dat `TO` inderdaad een kwadratische functie is.
-
Waarom is het uitwerken van de haakjes hier niet erg nuttig?
-
Breng de grafiek van `TO` in beeld. Welke vensterinstellingen gebruik je?
-
Ga met je rekenmachine na, dat de maximale opbrengst inderdaad bij `p=10` wordt gevonden.
Hoeveel bedraagt die maximale opbrengst?
Verwerken
-
Stel een voorschrift op van de lineaire functie waarvan de grafiek gaat door de punten `P(2,80)` en `Q(8,140)`.
-
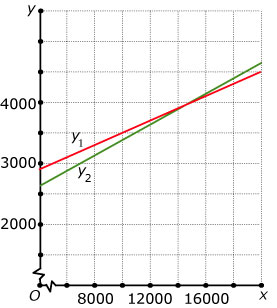
Je ziet de grafieken van de jaarlijkse kosten van twee verschillende auto’s.
Auto A was duurder in de aanschaf en heeft mede daarom hogere vaste kosten per jaar, maar is per gereden kilometer iets goedkoper.
-
Stel voor beide auto’s een passende formule op voor de jaarlijkse kosten als functie van het aantal gereden kilometers.
-
Bereken vanaf welk aantal gereden kilometers per jaar het voordeliger is om auto A aan te schaffen.
-
Twee cilindervormige kaarsen worden tegelijkertijd aangestoken. Ze branden gelijkmatig op. Een uur na het aansteken heeft kaars I een lengte van 75 cm en is kaars II nog 71 cm lang. 3, 5 uur na het aansteken worden beide kaarsen opnieuw gemeten: kaars I is dan 62,5 cm en kaars II is dan nog 61 cm lang.
-
Stel voor elk van deze kaarsen een formule op voor de lengte `L` in cm als functie van de brandtijd `t` in uren.
-
Hoeveel uur na het aansteken zijn beide kaarsen even lang?
-
Hoeveel uur na het aansteken verschillen ze 1 cm in lengte?
-
Een verfhandelaar heeft een mengmachine van € 300,- aangeschaft. Het mengen van verf kost hem naast deze vaste kosten nog € 6,- per liter.
-
Geef een formule voor de kosten `K` als functie van aantal liter verf `q` dat hij verkoopt.
-
Welke waarden kan `q` aannemen? Welke waarden kan `K` aannemen?
Hij verkoopt zijn gemengde verf voor € 8,25 per liter.
Zijn opbrengst R is ook een functie van q.
-
Welke formule geldt voor R?
-
Breng beide functies in beeld op je GR. Bereken het snijpunt van beide grafieken.
Welke betekenis heeft dit snijpunt voor de verfhandelaar?
-
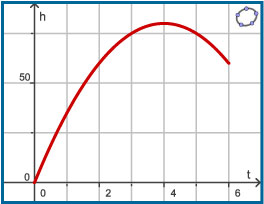
Een vuurpijl wordt vanaf de grond afgeschoten. De hoogte boven de grond hangt daarna tot hij uit elkaar spat af van de tijd. Er geldt: `h(t) = 40t - 5t^2`. Hierin is `h` de hoogte boven de grond in meter en `t` de tijd in seconden.
-
De vuurpijl spat na 6 seconden uit elkaar. Hoe hoog komt hij maximaal?
-
Schrijf domein en bereik van deze functie op, rekening houdend met de beschreven situatie.
-
Op welke hoogte spat de vuurpijl uit elkaar?
-
Hoeveel seconden is de vuurpijl zichtbaar boven een rij bomen van 40 m hoogte?
-
Waarom is de getekende grafiek niet de baan van de vuurpijl?
-
Gegeven is de functie `f` met `f(x) = -2(x - 10)^2 + 60` en domein `[0,40]`.
Bepaal het bereik van `f`.
Testen
-
Een echtpaar wil vanaf het station met de taxi naar huis. Ze kunnen kiezen tussen een treintaxi en een gewone taxi. De treintaxi kost € 3,00 per persoon. De gewone taxi rekent € 2,25 per rit en daarboven op nog € 0,75 per minuut.
-
Bij de gewone taxi is de ritprijs (`R`) afhankelijk van het aantal minuten (`a`) dat je er in zit.
Stel het bijbehorende functievoorschrift `R(a)` op.
-
Bij welke reistijd is het voordeliger om een treintaxi te nemen?
-
Taxi’s rijden in de stad gemiddeld 30 km/h. Wat raad je dit echtpaar aan als ze 5 km van het station wonen?
-
De grafiek van een lineaire functie gaat door de punten `A(-24,42)` en `B(30,16)`.
Stel een passend functievoorschrift op.

-
Hangbruggen zijn bruggen die zijn opgehangen aan zware spankabels.
Die spankabels hangen op hun beurt aan stalen masten of stenen torens.
Hier zie je een spankabel hangen tussen twee torens van 90 meter hoog.
Er geldt: `h(x) = frac{9}{50} x^2 + 5`.
-
Laat zien dat de tuidraad bij `x = 10` een lengte heeft van 23 meter.
-
Welk domein heeft de functie `h` in de beschreven situatie?
-
Welk bereik heeft de functie `h` dan?
-
Er zijn twee tuidraden met een lengte van 45,5 meter. Hoe ver hangen deze twee tuidraden van elkaar?
 Je ziet hier de punten P(10,210) en Q(30,300).
Je ziet hier de punten P(10,210) en Q(30,300).




 Je ziet hier de punten P(10,210) en Q(30,300).
Je ziet hier de punten P(10,210) en Q(30,300).
 Bekijk in Voorbeeld 2 hoe je het voorschrift opstelt van een lineaire functie als twee punten van de grafiek zijn gegeven.
Je ziet hier twee grafieken van lineaire functies. Stel voor elk van deze functies een passend voorschrift op en bereken algebraïsch het snijpunt van beide lijnen.
Bekijk in Voorbeeld 2 hoe je het voorschrift opstelt van een lineaire functie als twee punten van de grafiek zijn gegeven.
Je ziet hier twee grafieken van lineaire functies. Stel voor elk van deze functies een passend voorschrift op en bereken algebraïsch het snijpunt van beide lijnen.


