
Bijzondere functies
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Inleiding
Probeer de twee vragen bij Verkennen te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Uitleg
Opgaven
-
Bekijk de eerste pagina van de Uitleg.
Twee autoís rijden met een constante snelheid over dezelfde weg. Auto 1 gaat van `A` naar `B` met een constante snelheid van 90 km/h en auto 2 van `B` naar `A` met een constante snelheid van 120 km/h.
-
In de Uitleg wordt de afstand van beide autoís tot `A` bekeken.
Bekijk die afstand nu vanuit `B`. Schrijf de twee bijpassende formules op.
- Onderzoek door berekening of beide autoís elkaar nu op hetzelfde tijdstip tegenkomen.
-
Voor welke twee waarden van `t` bedraagt de onderlinge afstand van beide auto's 20 km?
-
Ga nu naar de tweede pagina van de Uitleg.
Daar zie je een mogelijke grafiek van een optrekkende auto.
-
Hoe zie je aan de grafiek dat de snelheid steeds toeneemt?
-
Met het schakelen naar een hogere versnelling is in de grafiek geen rekening gehouden. Hoe zie je dat?
-
Na hoeveel seconden is de gemiddelde snelheid ongeveer 60 km/h? (Ga er dus van uit dat er niet hoeft te worden geschakeld.)
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Theorie
Bestudeer de Theorie.
Er worden twee bijzondere soorten functies bekeken: lineaire en kwadratische functies.
Opgaven
-
Bekijk de Theorie.
Elke lineaire functie f heeft een functievoorschrift van de vorm `f(x) = ax + b`.
In de applet kun je de waarden van `a` en `b` aanpassen.
-
Welke betekenis heeft de `a` voor de grafiek van `f`?
-
Welke betekenis heeft de `b` voor de grafiek van `f`?
-
Welke waarden voor `a` en `b` moet je instellen om als grafiek een rechte lijn door `A(1,2)` en `B(5,3)` te krijgen?
-
Hoe kun je het bijbehorende functievoorschrift afleiden uit de coördinaten van `A` en `B`?
-
Ga nu naar Voorbeeld 1. Daar wordt een economisch model beschreven.
-
Heeft de gegeven formule inderdaad de vorm van een lineaire functie?
Wat is dan de richtingscoëfficiënt?
-
Maak een grafiek bij `q=4000-200p`. Welke vensterinstellingen gebruik je?
-
Bij welke prijs verkoopt hij 1500 exemplaren?
-
Voor een rit in een taxi betaal je voorrijkosten en een bedrag per gereden kilometer:
- voorrijkosten € 3,20
- per gereden km € 1,20
De ritprijs (`R`) hangt af van het aantal gereden kilometer (`a`).
-
Laat zien dat `R(10) = 15,2`.
-
Stel een voorschrift op voor de functie `R(a)`.
-
Dit is een voorbeeld van een lineaire functie. Teken de grafiek van deze functie op je grafische rekenmachine.
-
Waar vind je de twee getallen 3,20 en 1,20 in je grafiek terug?
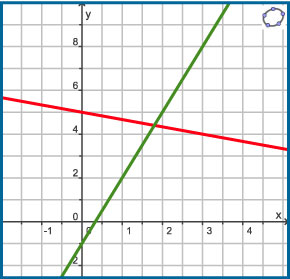 Bekijk in Voorbeeld 2 hoe je het voorschrift opstelt van een lineaire functie als twee punten van de grafiek zijn gegeven.
Je ziet hier twee grafieken van lineaire functies. Stel voor elk van deze functies een passend voorschrift op en bereken algebraïsch het snijpunt van beide lijnen.
Bekijk in Voorbeeld 2 hoe je het voorschrift opstelt van een lineaire functie als twee punten van de grafiek zijn gegeven.
Je ziet hier twee grafieken van lineaire functies. Stel voor elk van deze functies een passend voorschrift op en bereken algebraïsch het snijpunt van beide lijnen.
-
Voorbeeld 3 gaat over een kwadratische functie.
-
Laat door het uitwerken van de haakjes zien dat `TO` inderdaad een kwadratische functie is.
-
Waarom is het uitwerken van de haakjes hier niet erg nuttig?
-
Breng de grafiek van `TO` in beeld. Welke vensterinstellingen gebruik je?
-
Ga met je rekenmachine na, dat de maximale opbrengst inderdaad bij `p=10` wordt gevonden.
Hoeveel bedraagt die maximale opbrengst?
Verwerken
-
Stel een voorschrift op van de lineaire functie waarvan de grafiek gaat door de punten `P(2,80)` en `Q(8,140)`.
-
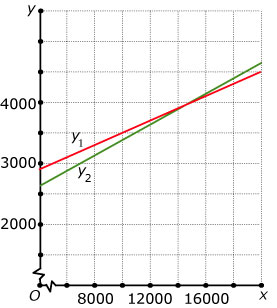
Je ziet de grafieken van de jaarlijkse kosten van twee verschillende autoís.
Auto A was duurder in de aanschaf en heeft mede daarom hogere vaste kosten per jaar, maar is per gereden kilometer iets goedkoper.
-
Stel voor beide autoís een passende formule op voor de jaarlijkse kosten als functie van het aantal gereden kilometers.
-
Bereken vanaf welk aantal gereden kilometers per jaar het voordeliger is om auto A aan te schaffen.
-
Twee cilindervormige kaarsen worden tegelijkertijd aangestoken. Ze branden gelijkmatig op. Een uur na het aansteken heeft kaars I een lengte van 75 cm en is kaars II nog 71 cm lang. 3, 5 uur na het aansteken worden beide kaarsen opnieuw gemeten: kaars I is dan 62,5 cm en kaars II is dan nog 61 cm lang.
-
Stel voor elk van deze kaarsen een formule op voor de lengte `L` in cm als functie van de brandtijd `t` in uren.
-
Hoeveel uur na het aansteken zijn beide kaarsen even lang?
-
Hoeveel uur na het aansteken verschillen ze 1 cm in lengte?
-
Een verfhandelaar heeft een mengmachine van € 300,- aangeschaft. Het mengen van verf kost hem naast deze vaste kosten nog € 6,- per liter.
-
Geef een formule voor de kosten `K` als functie van aantal liter verf `q` dat hij verkoopt.
-
Welke waarden kan `q` aannemen? Welke waarden kan `K` aannemen?
Hij verkoopt zijn gemengde verf voor € 8,25 per liter.
Zijn opbrengst R is ook een functie van q.
-
Welke formule geldt voor R?
-
Breng beide functies in beeld op je GR. Bereken het snijpunt van beide grafieken.
Welke betekenis heeft dit snijpunt voor de verfhandelaar?
-
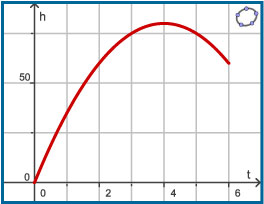
Een vuurpijl wordt vanaf de grond afgeschoten. De hoogte boven de grond hangt daarna tot hij uit elkaar spat af van de tijd. Er geldt: `h(t) = 40t - 5t^2`. Hierin is `h` de hoogte boven de grond in meter en `t` de tijd in seconden.
-
De vuurpijl spat na 6 seconden uit elkaar. Hoe hoog komt hij maximaal?
-
Schrijf domein en bereik van deze functie op, rekening houdend met de beschreven situatie.
-
Op welke hoogte spat de vuurpijl uit elkaar?
-
Hoeveel seconden is de vuurpijl zichtbaar boven een rij bomen van 40 m hoogte?
-
Waarom is de getekende grafiek niet de baan van de vuurpijl?
-
Gegeven is de functie `f` met `f(x) = -2(x - 10)^2 + 60` en domein `[0,40]`.
Bepaal het bereik van `f`.
Testen
-
Een echtpaar wil vanaf het station met de taxi naar huis. Ze kunnen kiezen tussen een treintaxi en een gewone taxi. De treintaxi kost € 3,00 per persoon. De gewone taxi rekent € 2,25 per rit en daarboven op nog € 0,75 per minuut.
-
Bij de gewone taxi is de ritprijs (`R`) afhankelijk van het aantal minuten (`a`) dat je er in zit.
Stel het bijbehorende functievoorschrift `R(a)` op.
-
Bij welke reistijd is het voordeliger om een treintaxi te nemen?
-
Taxiís rijden in de stad gemiddeld 30 km/h. Wat raad je dit echtpaar aan als ze 5 km van het station wonen?
-
De grafiek van een lineaire functie gaat door de punten `A(-24,42)` en `B(30,16)`.
Stel een passend functievoorschrift op.

-
Hangbruggen zijn bruggen die zijn opgehangen aan zware spankabels.
Die spankabels hangen op hun beurt aan stalen masten of stenen torens.
Hier zie je een spankabel hangen tussen twee torens van 90 meter hoog.
Er geldt: `h(x) = frac{9}{50} x^2 + 5`.
-
Laat zien dat de tuidraad bij `x = 10` een lengte heeft van 23 meter.
-
Welk domein heeft de functie `h` in de beschreven situatie?
-
Welk bereik heeft de functie `h` dan?
-
Er zijn twee tuidraden met een lengte van 45,5 meter. Hoe ver hangen deze twee tuidraden van elkaar?

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Inleiding
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Uitleg
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Functies en grafieken > Bijzondere functies > Theorie
 Bekijk in Voorbeeld 2 hoe je het voorschrift opstelt van een lineaire functie als twee punten van de grafiek zijn gegeven.
Je ziet hier twee grafieken van lineaire functies. Stel voor elk van deze functies een passend voorschrift op en bereken algebraïsch het snijpunt van beide lijnen.
Bekijk in Voorbeeld 2 hoe je het voorschrift opstelt van een lineaire functie als twee punten van de grafiek zijn gegeven.
Je ziet hier twee grafieken van lineaire functies. Stel voor elk van deze functies een passend voorschrift op en bereken algebraïsch het snijpunt van beide lijnen.


