Totaalbeeld

Samenvatten

Je hebt nu alle theorie van "Redeneren en bewijzen" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:
11: definitie — vermoeden — axioma — bewijs (uit het ongerijmde)
12: congruentie — congruentiekenmerken driehoeken — driehoeksongelijkheid
13: gegeven, te bewijzen, bewijs als structuur van een bewijs — direct en indirect (uit het ongerijmde) bewijs
14: gelijkvormigheid — gelijkvormigheidskenmerken van driehoeken
15: hoogtelijn, zwaartelijn, bissectrice (deellijn), loodlijn, middelloodlijn, middenparallel (in driehoeken)

Activiteitenlijst:
11: eenvoudige bewijzen leveren vanuit basisdefinities en axioma's
12: congruentiekenmerken van driekhoeken gebruiken in bewijzen
13: bewijzen leveren volgens een vaste structuur — werken vanuit de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B
14: werken met gelijkvormige driehoeken in bewijzen
15: de eigenschappen van bijzondere lijnen bewijzen

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Totaalbeeld > Achtergronden

Testen

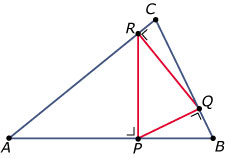  1. Bekijk deze figuur.
    Bewijs dat `Delta PQR` gelijkvormig is met `Delta ABC`.

  2. Gegeven is een driehoek `ABC`. Op `AC` wordt een gelijkzijdige driehoek `ACD` en op `BC` wordt een gelijkzijdige driehoek `BCE` gemaakt. `/_ACD = /_BCE` en beide gelijkzijdige driehoeken overlappen driehoek `ABC` niet.
    Bewijs dat `BD = AE`.

  3. `l`, `m` en `n` zijn drie evenwijdige lijnen, `m` tussen `l` en `n`. De lijn `s` staat loodrecht op `l` en snijdt `l`, `m` en `n` in respectievelijk `A`, `B` en `C`. `|AB| : |BC| = 1 : 3`. Je gaat bewijzen dat van elke lijn die de drie lijnen snijdt het stuk tussen `l` en `n` door `m` verdeeld wordt in stukken die zich verhouden als `1 : 3`.
    1. Bewijs eerst dat `s` ook `m` en `n` loodrecht snijdt.
    2. Bekijk een lijn `t` die ook loodrecht op `l` staat. Geef voor dat geval een bewijs. Gebruik rechthoeken, hulplijnen, congruentie en gelijkvormigheid.
    3. Neem nu een lijn die niet loodrecht op `l` staat. Geef voor dat geval een bewijs, gebruik hulplijnen.

  4. In `Delta ABC` zijn `AD`, `BE` en `CF` de hoogtelijnen.
    Bewijs dat deze hoogtelijnen bissectrices zijn in `Delta DEF`.

  5. Gegeven is een gelijkbenige driehoek `ABC` met `|AB| = |AC| = 8` en `|BC| = 4`.
    Bereken de straal van de ingeschreven cirkel (dat is de cirkel die alle zijden van de driehoek raakt).

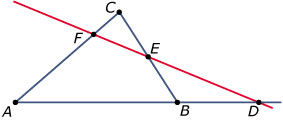
  6. De stelling van Menelaos

    De drie (verlengde) zijden van een driehoek `ABC` worden gesneden door een lijn `m`. Het snijpunt van (het verlengde) van `AB` met `m` is punt `D`, het snijpunt van (het verlengde) van `BC` met `m` is punt `E` en het snijpunt van (het verlengde) van `AC` met `m` is punt `F`. Bewijs dat nu geldt: `(|AD|)/(|BD|) * (|BE|)/(|CE|) * (|CF|)/(|AF|) = 1`. Dit is een variant van een uitgebreidere stelling die wordt toegeschreven aan Menelaos van Alexandrië (70 - 140 na Chr.).
    1. In de getekende situatie ligt alleen `D` op het verlengde van `AB`. Lever eerst voor deze situatie het bewijs. (Aanwijzing: trek een lijn door hoekpunt `C` en evenwijdig met `AB`, deze lijn snijdt `m` in punt `G`.)
    2. Teken nu een situatie waarin niet alleen `D` op het verlengde van `AB`, maar ook `E` op het verlengde van `BC` en `F` op het verlengde van `AC` ligt. Lever ook voor die situatie een bewijs.

Toepassen

  1. Constructies met passer en liniaal

    Onder de constructie van een figuur wordt in de vlakke meetkunde verstaan het tekenen van de figuur met behulp van uitsluitend een liniaal (zonder maatindeling) en een passer. Zie

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Totaalbeeld > Toepassingen

    Voer de onderstaande constructies zelf uit en bewijs dat ze inderdaad het gewenste resultaat opleveren.
    1. Een loodlijn van een punt `P` op een lijn `l` construeer je door eerst een cirkel met middelpunt `P` te maken, zo groot dat hij `l` in twee punten snijdt. Noem die punten `A` en `B`. Vervolgens maak je met middelpunt `A` en daarna met middelpunt `B` een even grote cirkel. Het snijpunt van die cirkels is `S`. En `PS` staat loodrecht op `l`.
    2. De middelloodlijn van lijnstuk `AB` construeer je door twee even grote cirkels met middelpunten `A` en `B` met elkaar te snijden. (De straal van deze cirkels moet groter zijn dan de helft van de lengte van lijnstuk `AB`). Als hun snijpunten `P` en `Q` zijn is lijn `PQ` de middelloodlijn van `AB`.
    3. Voor de constructie van de bissectrice van `/_A` met benen `l` en `m`, ga je als volgt te werk.
      Open de passer een stukje en beschrijf een cirkel met middelpunt `A`. Die snijdt `l` en `m`, zeg in `B` respectievelijk `C` (je hoeft daarvoor niet de hele cirkel te tekenen). Zonder de stand van de passer te veranderen maak je nu een cirkel met middelpunt `B` en een met middelpunt `C` en bepaalt hun snijpunt `D`. Dan is `AD` de gezochte bissectrice.

  2. Voronoi-diagrammen

    Bij mobiele telefonie wordt contact gemaakt met de dichtstbij zijnde antenne die de telefoon herkent. Om elke antenne bestaat een gebied waarvan de punten juist tot deze antenne de kortste afstand hebben. De grenzen van deze gebieden zijn (stukken van) middelloodlijnen. Je spreekt wel van een voronoidiagram. Lees er meer over in

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Totaalbeeld > Toepassingen

    Je ziet daar hoe een voronoidiagram wordt gemaakt met 8 punten.
    1. Teken een voronoidiagram met 3 punten. In welke situatie gaan de drie grenslijnen niet door één punt?
    2. Je wilt een voronoidiagram maken met 4 punten. Hoeveel middelloodlijnen spelen er dan een rol?
    3. Teken drie voronoidiagrammen met 4 punten, bij één ervan gaan de grenslijnen door één punt en bij een andere lopen alle grenslijnen evenwijdig.

  3. De rechte van Euler

    Teken je in een driehoek het snijpunt H van de hoogtelijnen, het snijpunt Z van de zwaartelijnen en het snijpunt M van de middelloodlijnen, dan blijken die drie punten op één rechte lijn te liggen, de zogenaamde rechte van Euler. Bekijk de animatie op

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Totaalbeeld > Toepassingen

    Probeer een bewijs te vinden voor deze stelling. Zoek rustig op internet, maar formuleer het bewijs op je eigen manier en zo dat je het begrijpt.

Examenopgaven

  1. Driehoek en cirkel

    In de figuur hiernaast is een scherphoekige driehoek `ABC` getekend, met `AC > AB`, en de cirkel met middelpunt `A` en straal `AB`. Deze cirkel snijdt `BC` in `D` en `AC` in `E`. De grootte van `/_BAC` noemen we `alpha`.
    Druk `/_CDE` uit in `alpha`. Bewijs dat je antwoord juist is.

    (bron: examen wiskunde A vwo 2008, tweede tijdvak)