Totaalbeeld

Antwoorden bij de opgaven

  1. Gegevens en te bewijzen: zie opgave en figuur.
    Bewijs: Uit `/_A + /_PRA = 90^(text(o))` en `/_QRP + /_PRA = 90^(text(o))` volgt `/_QRP = /_A`. Uit `/_B + /_BPQ = 90^(text(o))` en `/_QPR + /_BPQ = 90^(text(o))` volgt `/_QPR = /_B`. En daaruit volgt `Delta PQR ~ Delta ABC` (hh). Q.e.d.
  2. Gegeven: `Delta ABC` en de gelijkzijdige driehoeken `ACD` en `BCE` (die niet overlappen met `Delta ABC`).
    Te bewijzen: `AE = BD`.
    Bewijs: De hoeken van de gelijkzijdige driehoeken zijn allemaal 60° (stelling gelijkzijdige driehoek).
    `|CE| = |CB|`, `|CD| = |CA|` en `/_ACE = /_ACB + 60^(text(o)) = /_BCD` geeft `Delta AEC ~= Delta DBC` (ZHZ). En dus is `|AE| = |BD|`. Q.e.d.
    1. Gegeven is dat `s` de lijnen `l`, `m` en `n` snijdt in de punten `A`, `B` en `C`.
      Omdat `m` en `n` evenwijdig zijn met `l` zijn de hoeken bij de snijpunten ook 90° (F-hoeken).
    2. Lijn `t` staat loodrecht op lijn `l` en dus staat `t` loodrecht op `m` en `n` (F-hoeken).
      De snijpunten van `t` met `l`, `m` en `n` zijn respectievelijk `D`, `E` en `F`. Dan zijn `ABED` en `BCFE` rechthoeken (definitie rechthoek). Dus is `|AB| = |DE|` en `|BC| = |EF|` en is ook `|BC| : |EF| = 1 : 3`.
    3. Lijn `u` staat niet loodrecht op `l` en gaat door `D`. De snijpunten van `u` met `m` en `n` zijn respectievelijk `G` en `H`.
      Met behulp van F-hoeken is `Delta DEG ~ Delta DFH`, zodat `|DE| : |DF| = 1 : 4 = |DG| : |DH|`.
      En daaruit volgt `|DG| : |GH| = 1 : 3`.
  4. Gegeven: `Delta ABC` met hoogtelijnen `AD`, `BE` en `CF` en `Delta DEF`.
    Te bewijzen: `AD`, `BE` en `CF` zijn bissectrices van `Delta DEF`.
    Bewijs: Omdat `/_C = /_C` en `/_ADC = /_BEC = 90^(text(o))` is `Delta ADC ~ Delta BEC` (hh) en dus is ``(|AC|)/(|BC|) = (|DC|)/(|EC|)`. Uit dit laatste volgt samen met `/_C = /_C` dat `Delta EDC ~ Delta BAC` (zhz) en dus dat `/_EDC = /_A` en `/_DEC = /_B`.
    Op dezelfde manier bewijs je dat `/_FDB = /_A` en `/_DFB = /_C`. En ook dat `/_AFE = /_C` en /_AEF = /_B.
    En daaruit volgt: `/_CFD = 90^(text(o)) - /_B = /_EFC` en dus is `CF` bissectrice van `/_EFD`.
    Enzovoorts...
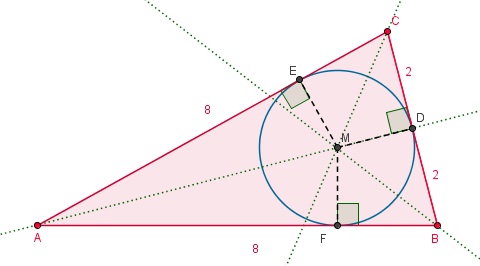  5. Zie de figuur hiernaast.
    De ingeschreven cirkel heeft als middelpunt het snijpunt `M` van de bissectrices en als straal `MD = ME = MF = r`. Gebruik nu de gelijkvormige driehoeken `ABD` en `AME` (hh).
    Pythagoras: `AD = sqrt(8^2 - 2^2) = sqrt(60)`.
    `r/2 = (sqrt(60) - r)/8` geeft `r = 0,2 sqrt(60)`.
    1. Gegeven: `Delta ABC` met `D` op het verlengde van `AB`, `E` op `BC` en `F` het snijpunt van lijn `DE` en zijde `AC`. (Lijn `DE` is lijn `m`.)
      Te bewijzen: `(|AD|)/(|BD|) * (|BE|)/(|CE|) * (|CF|)/(|AF|) = 1`. Bewijs: Teken lijn `n` door `C` en evenwijdig `AB`. `G` is het snijpunt van `m` en `n`.
      Omdat `/_FGC = /_BDE` en `/_ECG = /_BDE` (Z-hoeken) is `Delta GEC ~ Delta DEB` en dus `(|CF|)/(|AF|) = (|CG|)/(|AD|)`.
      Omdat `/_FGC = /_BDE` en `/_FCG = /_DAF` (Z-hoeken) is `Delta GFC ~ Delta DFA` en dus `(|CG|)/(|BD|) = (|CE|)/(|BE|)`.
      Hieruit volgt `(|CF|)/(|AF|) * |AD| = (|CE|)/(|BE|) * |BD|` en daaruit volgt `(|AD|)/(|BD|) * (|BE|)/(|CE|) * (|CF|)/(|AF|) = 1`. Q.e.d.
    2. Gaat op een vergelijkbare manier, weer teken je dezelfde hulplijn.
    1. Uit `PA = PB`, `AS = BS` en `PS = PS` volgt dat `Delta PAS ~= Delta PBS`, dus is `Delta PAB` gelijkbenig met `PS` als bissectrice van `/_APB`. Als `M` het snijpunt van `PS` en `AB` is betekent dit dat ook `Delta PAM ~= Delta PBM` (ZHZ). En dus is `/_AMP = /_ BMP = 90^(text(o))`.
    2. Nu is `AQBP` een ruit en dus staan de diagonalen loodrecht op elkaar en delen ze elkaar middendoor (stelling ruit en stelling parallellogram).
    3. Nu is `ABDC` een ruit en wordt `/_A` door diagonaal `AD` middendoor gedeeld (stelling ruit).
    1. Wordt een driehoek met de drie middelloodlijnen door één punt, tenzij de punten op één rechte lijn liggen. In dat laatste geval krijg je twee parallelle middelloodlijnen.
    2. Er zijn nu `(4 * 3)/2 = 6` middelloodlijnen in totaal.
    3. -
  9. Globale opzet van het bewijs:
    Noem `D`, `E`, `F` de middens van respectievelijk `BC`, `AC` en `AB` en toon aan dat `Delta DEF ~ Delta ABC` met een vergrotingsfactor van `-0,5`. De zwaartelijnen van `Delta ABC` zijn dat ook in `Delta DEF`, dus het zwaartepunt is voor beide driehoeken `Z`. De middelloodlijnen van `Delta ABC` worden de hoogtelijnen van `Delta DEF`, dus de vermenigvuldiging van `Delta ABC` t.o.v. van punt `Z` met `-0,5` laat `H` overgaan in `M` en omgekeerd. Niet alleen liggen dus de drie punten op één lijn, maar ook geldt: `MZ : HZ = 1 : 2`.
  10. Zie figuur, teken lijnstuk `ED`.
    Nu is `/_ADB = /_ABD = 90^(text(o)) - 1/2 /_BAD`.
    Evenzo: `/_ADE = /_AED = 90^(text(o)) - 1/2 /_EAD`.
    En dus is `/_CDE = 180^(text(o)) - (90^(text(o)) - 1/2 /_BAD) - (90^(text(o)) - 1/2 /_EAD) = 1/2 (/_BAD + /_EAD) = 1/2 alpha`.