Bijzondere lijnen

Inleiding

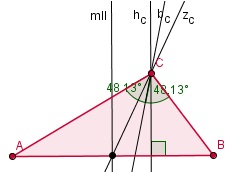
Je ziet hier in een ΔABC de hoogtelijn uit C, de zwaartelijn uit C, de bissectrice (deellijn) van ∠C en de middelloodlijn van AB. Verander je de driehoek, dan kunnen een aantal van deze lijnen gaan samenvallen. Verder kun je in elke driehoek drie van elk van die soorten lijn(stukk)en tekenen.
Welke eigenschappen hebben ze?

Je leert nu:

Je kunt al:

Verkennen

Bekijk de figuur hierboven nog eens.

> Bij welke soort driehoeken vallen de vier getekende lijnen samen?
> Kun je een driehoek maken waarbij alleen de bissectrice uit C en de hoogtelijn uit C samenvallen?

Uitleg

Je ziet hier in een ΔABC de hoogtelijn uit C, de zwaartelijn uit C, de bissectrice (deellijn) van ∠C en de middelloodlijn van AB. Verander je de driehoek, dan kunnen een aantal van deze lijnen gaan samenvallen.
Allereerst moet goed worden vastgelegd wat je onder elk van deze lijnen verstaat. En er zijn nog meer bijzondere lijnen, namelijk de loodlijn en de middenparallel. Hun definities vind je in de theorie en ook op je lijst van definities/stellingen in de Vlakke Meetkunde.

Merk op dat de vier getekende lijnen alleen samenvallen als AC = BC, dus als ΔABC gelijkbenig is met tophoek C. Dit zijn eigenlijk twee stellingen:

Je zegt wel dat het samenvallen van de vier genoemde lijnen en de eigenschap AC = BC equivalent of gelijkwaardig zijn. Dit is alleen het geval als met een stelling ook zijn omgekeerde waar is.

‡

Opgaven

  1. In de Uitleg zie je een zwaartelijn in een driehoek `ABC`.
    1. Teken een driehoeken `ABC` met daarin alle drie de zwaartelijnen.
    2. Gaan de drie zwaartelijnen door één punt? Kun je dit bewijzen?

  2. Bewijs: Als in een driehoek de hoogtelijn en de zwaartelijn uit hetzelfde hoekpunt samenvallen, dan is die lijn ook bissectrice van deze hoek en is de driehoek gelijkbenig.

  3. Bewijs de volgende stellingen over hoogtelijnen, zwaartelijnen en bissectrices in een gelijkbenige driehoek.
    1. In een gelijkbenige driehoek zijn er twee even lange hoogtelijnen.
    2. In een gelijkbenige driehoek zijn er twee even lange zwaartelijnen.
    3. In een gelijkbenige driehoek zijn er twee even lange bissectrices.

Theorie

De definities van een aantal bijzondere lijnen zijn:

Deze definities staan ook op de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B.

In een driehoek kun je drie middelloodlijnen, drie bissectrices, drie zwaartelijnen, drie hoogtelijnen en ook drie middenparallellen tekenen. Bij bepaalde driehoeken vallen meerdere van die lijnen samen, vaak gaan ze door één punt. Ze hebben bepaalde eigenschappen die je met behulp van congruentie en gelijkvormigheid kunt bewijzen.

‡

Voorbeeld 1

Bewijs dat de bissectrices van de drie hoeken van een driehoek elkaar in één punt snijden en dat dit punt gelijke afstanden heeft tot elk van de zijden van de driehoek.

Antwoord

Gegeven:
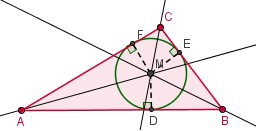
Zie figuur. AM en BM zijn bissectrices; CM is de lijn door C en M.

Te bewijzen:
MD = ME = MF en lijn CM is bissectrice.

Bewijs:
Omdat AM bissectrice van ∠A is, geldt: ∠DAM = ∠FAM. Verder is AM = AM en ∠ADM = ∠AFM = 90°. Dus zijn ΔDAM en ΔFAM congruente driehoeken (ZHH).
Dit betekent MD = MF.
Op vergelijkbare wijze is MD = ME.
Omdat CM = CM, MF = ME en ∠CEM = ∠CFM = 90° zijn ΔCEM en ΔCFM congruent (ZZR).
En dus is ∠ECM = ∠FCM en is CM bissectrice van ∠C.
Q.e.d.

‡

Voorbeeld 2

Bewijs dat de zwaartelijnen van een driehoek elkaar in één punt snijden en dat dit punt de zwaartelijnen verdeelt in stukken die zich verhouden als 1 : 2.

Antwoord

Gegeven:
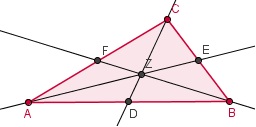
AE, BF en CD zijn zwaartelijnen, dus BE = EC, AF = FC en AD = DB. Z is het snijpunt van AE en BF.

Te bewijzen:
CD gaat door Z en FZ : ZB = EZ : ZA = CD : ZC = 1 : 2.

Bewijs:
CA = 2 · CF en CB = 2 · CE, dus ΔABC is gelijkvormig met ΔFEC (hh). Dit betekent: AB = 2 · FE en AB // EF. Hieruit volgt: ∠BAE = ∠AEF en ∠ABF = ∠BFE (Z-hoeken). En dus is ΔABZ gelijkvormig met ΔEFZ (hh).
Omdat AB = 2 · FE is FZ : ZB = 1 : 2 = EZ : ZA. De zwaartelijnen AE en BF verdelen elkaar dus in de verhouding 1 : 2.
Eenzelfde redenering geldt voor bijvoorbeeld de zwaartelijnen AE en CD. En dus moet CD wel door punt Z gaan. Alle drie de zwaartelijnen gaan door één punt Z, het zwaartepunt van de driehoek. Q.e.d.

‡

Voorbeeld 3

Bewijs dat de bissectrice een hoek in een driehoek de tegenoverliggende zijde verdeeld in stukken die zich verhouden als de zijden op de benen van die hoek.

Antwoord

Gegeven:
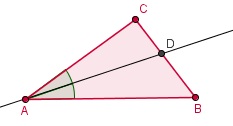
Zie figuur. ∠BAD = ∠CAD

Te bewijzen:
BD / CD = AB / AC

Bewijs:
Trek een lijn door C en evenwijdig AB.
Punt E is het snijpunt van de bissectrice met deze lijn.
Nu is ∠CED = ∠BAD (Z-hoeken) en dus is AC = CE (gelijkbenige driehoek AEC).
Verder zijn de driehoeken ABD en ECD gelijkvormig (hh).
Dus: BD / CD = AB / EC = AB / AC.
Q.e.d.

‡

Opgaven

  1. In Voorbeeld 1 wordt bewezen dat de drie bissectrices van een driehoek `ABC` door één punt gaan.
    1. Loop het bewijs na. Welke congruentiekenmerken worden gebruikt?
    2. Waarom kun je een cirkel trekken met middelpunt `M` die precies alle drie de zijden van `Delta ABC` raakt?

  2. Teken (met GeoGebra of maak een paar voorbeelden) een driehoek `ABC` met daarin de drie middelloodlijnen van de zijden.
    1. Bewijs dat deze drie middelloodlijnen door één punt `M` gaan.
    2. Ligt punt `M` altijd binnen de driehoek? Wanneer wel en wanneer niet?
    3. Waarom kun je een cirkel met middelpunt `M` tekenen door de hoekpunten van de driehoek?
    4. Waarom kun je door drie willekeurige punten die niet op één rechte lijn liggen altijd een cirkel tekenen?

  3. In Voorbeeld 2 wordt bewezen dat de drie zwaartelijnen van een driehoek `ABC` door één punt gaan.
    1. Teken een driehoek `ABC` met daarin de drie hoogtelijnen.
    2. Bewijs dat die drie hoogtelijnen door één punt gaan. Teken daartoe `Delta DEF` door een lijn door `A` en evenwijdig `BC`, door `B` en evenwijdig `AC`en door `C`een lijn evenwijdig aan `AB` te trekken. Gebruik het resultaat van de vorige opgave.

  4. Bekijk het bewijs dat een bissectrice van een hoek in een driehoek de overstaande zijde verdeelt in stukken met dezelfde verhouding als de zijden op de benen van die hoek, zie Voorbeeld 3.
    1. Voer zelf dit bewijs uit voor de bissectrice van `/_C`.
    2. Stel je voor dat in `Delta ABC` geldt: `|AB| = 8`, `|BC| = 4` en `|AC| = 6`. `BD` is de bissectrice van `/_B`. Bereken de lengtes van `AD` en `CD`.

Verwerken

  1. `A` en `B` zijn punten van een cirkel. Bewijs dat de middelloodlijn van `AB` door het middelpunt `M` van de cirkel gaat.

  2. Bewijs: Een driehoek die twee gelijke zwaartelijnen heeft is gelijkbenig.
    (Je kunt hier werken met de stelling dat de zwaartelijnen in een driehoek elkaar verdelen in een verhouding van 1 : 2.)

  3. In `Delta ABC` is `h_A` de lengte van de hoogtelijn uit `A` op `BC` en `h_B` die op `AC`. `|BC| = a` en `|AC| = b`.
    1. Bewijs met gelijkvormigheid dat `h_A : h_B = b : a`.
    2. Bewijs deze stelling ook door formules voor de oppervlakte van een driehoek te gebruiken.

  4. Een hoek in een driehoek heeft twee buitenhoeken. Dat zijn de hoeken met de verlengde van de zijden. De hoek zelf en een buitenhoek zijn dus samen altijd 180°. De bissectrice van een buitenhoek heet de buitenbissectrice van die hoek.
    1. Bewijs dat bij een driehoek `ABC` de bissectrice van `/_A` en de buitenbissectrices bij `B` en `C` door één punt gaan.
    2. Bewijs dat de bissectrice van de hoek loodrecht staat op de buitenbissectrice van de bijbehorende buitenhoek.
    3. Bewijs: als in een hoekpunt van een driehoek de buitenbissectrice loodrecht staat op de zwaartelijn vanuit dat hoekpunt, dan is de driehoek gelijkbenig.

Testen

  1. In `Delta ABC` is `D` het snijpunt van de hoogtelijn uit `A` op `BC` en `E` het snijpunt van de hoogtelijn uit `B` op `AC`.
    Gegeven is dat `/_A > 90`°. Bewijs dat `/_ABC = /_DEC`.

  2. Van een driehoek is gegeven dat voor twee van zijn zijden geldt: hun middelloodlijn gaat door het overstaande hoekpunt. Toon aan dat de driehoek gelijkzijdig is.