
Gelijkvormigheid
Inleiding
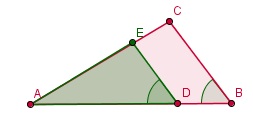
Hier zie je twee gelijkvormige driehoeken ABC en ADE.
Van gelijkvormigheid kun je bij bewijzen (en berekeningen) vaak goed gebruik maken. Maar wanneer zijn twee driehoeken nu precies gelijkvormig?
Je leert nu:
- gelijkvormige driehoeken herkennen;
- bewijzen leveren met de gelijkvormigheidskenmerken.
Je kunt al:
- eenvoudige bewijzen leveren vanuit de lijst met definities/stellingen voor Vlakke Meetkunde.
- gebruik maken van congruentie en de congruentiekenmerken van driehoeken.
Verkennen
Hier zie je twee gelijkvormige driehoeken ABC en ADE.
Van gelijkvormigheid kun je bij bewijzen (en berekeningen) vaak goed gebruik maken. Maar wanneer zijn twee driehoeken nu precies gelijkvormig?
> Kun je gelijkvormigheidskenmerken formuleren op dezelfde wijze als de congruentiekenmerken?
Uitleg
Twee driehoeken heten gelijkvormig als de éne driehoek een vergroting of verkleining is van de andere driehoek.
Hier zie je twee driehoeken ABC en ADE.
De hoeken ∠BAC en ∠DAE zijn gelijk.
De zijden om die hoek hebben in ΔABC dezelfde verhouding als in ΔADE: AB / AC = AD / AE.
Je kunt nu bewijzen dat beide driehoeken gelijkvormig zijn.
Immers je kunt AD vermenigvuldigen met een zodanige factor dat hij gelijk is aan AB. Vermenigvuldig je AE met dezelfde factor, dan wordt AE gelijk aan AC. De hoek ∠DAE laat je hetzelfde. Op grond van het congruentiekenmerk ZHZ zijn beide driehoeken dan congruent. En dus is ΔABC een vergroting van ΔADE.
Het gelijkvormigheidskenmerk dat je nu hebt bewezen is zhz: beide driehoeken hebben een even grote hoek en de zijden die die hoek insluiten hebben dezelfde verhouding.
Op vergelijkbare wijze kun je nog drie gelijkvormigheidskenmerken afleiden.
‡
Opgaven
-
In de Uitleg wordt een begin gemaakt met het afleiden van gelijkvormigheidskenmerken.
- Teken de driehoeken `ABC` en `DEF` zo, dat `/_A = /_D`, `/_B = /_E` en `AB != DE`.
- Bekijk nu driehoek `ABC`. Vergroot alle zijden van die driehoek door ze te vermenigvuldigen met `(DE)/(AB)`. Je krijgt dan de driehoek `AB'C'`.
- Leg uit waarom driehoek `AB'C'` congruent is met driehoek `DEF`.
- Waarom volgt hieruit dat de driehoeken `ABC` en `DEF` gelijkvormig zijn?
- Dit gelijkvormigheidskenmerk wordt aangeduid met hh. Waarom niet met hhh?
-
Zijn congruente driehoeken altijd gelijkvormig? Geldt het omgekeerde ook?
Theorie
Twee driehoeken heten gelijkvormig als de éne driehoek een vergroting of verkleining is van de andere driehoek. Ze hebben dan dezelfde hoeken en de verhoudingen van hun zijden zijn gelijk.
Of twee driehoeken gelijkvormig zijn volgt uit deze gelijkvormigheidskenmerken.
Twee driehoeken zijn gelijkvormig als ze gelijk hebben:
- twee paren hoeken (hh);
- één paar hoeken en de verhouding van de omliggende zijden (zhz);
- de verhoudingen van de zijden (zzz);
- één paar rechte hoeken en de verhouding van twee niet omliggende zijden (zzr).
Een paar zijden (hoeken) betekent hier steeds een zijde (hoek) van de éne driehoek en de overeenkomstige zijde (hoek) van de andere driehoek. Deze gelijkvormigheidskenmerken staan ook op de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B. Merk op dat er nu steeds kleine letters worden gebruikt om er naar te verwijzen in tegenstelling tot de congruentiekenmerken.
De gelijkvormigheidskenmerken zijn telkens af te leiden uit de congruentiekenmerken.
‡
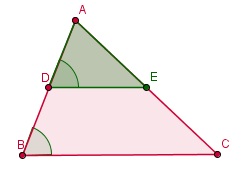
Voorbeeld 1
Bewijs dat de lengte van een lijnstuk vanuit het midden van een zijde van een driehoek en evenwijdig met een andere zijde van die driehoek een lengte heeft die gelijk is aan de helft van de lengte van de zijde waaraan het evenwijdig is.
Zo'n lijnstuk heet een middenparallel in de gegeven driehoek.
Antwoord
Gegeven:
D is het midden van AB en DE // BC.
Te bewijzen:
|DE| = |BC|.
Bewijs:
Omdat DE // BC is ∠ADE = ∠ABC en ∠DEA = ∠BCA (F-hoeken).
Dus zijn ΔABC en ΔADE gelijkvormig (hh).
De zijden van beide driehoeken hebben daarom dezelfde verhoudingen, namelijk 1 : 2. En dus is |DE| = |BC|.
Q.e.d.
‡
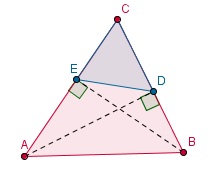
Voorbeeld 2
In ΔABC zijn de hoogtelijnen AD en BE getrokken.
Bewijs dat ΔDEC gelijkvormig is met ΔABC.
Antwoord
Gegeven:
∠ADC = ∠BEC = 90°.
Te bewijzen:
ΔDEC is gelijkvormig met ΔABC.
Bewijs:
Omdat ∠ADC = ∠BEC = 90° en ∠C = ∠C zijn ΔADC en ΔBEC gelijkvormig (hh).
En daarom is CD / AC = CE / CB.
Vanwege deze gelijke verhoudingen en ∠C = ∠C zijn ΔABC en ΔDEC gelijkvormig (zhz).
‡
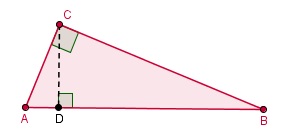
Voorbeeld 3
ΔABC heeft in C een rechte hoek.
Bewijs dat AC2 + BC2 = AB2.
Antwoord
Gegeven:
∠ACB = 90°. Je tekent hoogtelijn CD, dus ook ∠ADC = ∠CDB = 90°.
Te bewijzen:
AC2 + BC2 = AB2.
| ΔABC | AB | BC | AC |
| ΔCBD | BC | BD | CD |
| ΔACD | AC | CD | AD |
Bewijs:
De driehoeken ABC, CBD en ACD zijn gelijkvormig (hh).
De verhoudingen van hun zijden zijn daarom gelijk, dus je kunt deze verhoudingstabel maken.
Hieruit kun je afleiden:
BC2 = AB · BD en AC2 = AB · AD.
Dus: AC2 + BD2 = AB · BD + AB · AD = AB · (BD + AD) = AB2.
Je ziet: een geheel nieuw bewijs van de stelling van Pythagoras!
‡
Opgaven
-
In Voorbeeld 1 wordt de stelling bewezen dat een middenparallel binnen een driehoek de helft is van de zijde waaraan hij evenwijdig is.
-
Loop het bewijs na. Welk gelijkvormigheidskenmerk wordt gebruikt?
-
Teken de lijnstukken `BE` en `CD`. Deze lijnstukken snijden elkaar in punt `S`. Welke twee gelijkvormige driehoeken ontstaan nu?
- Bekijk
Voorbeeld 2.
-
Maak een verhoudingstabel van de zijden van de driehoeken `ABC` en `DEC`. Ga na, dat bij deze tabel ook inderdaad `CD // AC = CE // CB` past.
-
Gegeven is `AB = 6`, `BC = 4` en `ED = 2,5`. Welke van beide andere zijden van `Delta DEC` kun je met deze gegevens berekenen? Voer die berekening uit.
-
In Voorbeeld 3 vind je een ander bewijs van de stelling van Pythagoras.
- Neem aan dat `AC = 5` en `BC = 12`. Bereken de lengte van `CD`.
- Bewijs dat in een rechthoekige driehoek het kwadraat van de hoogtelijn op de hypothenusa gelijk is aan het product van de lengtes waarin hij die hypothenusa verdeelt.
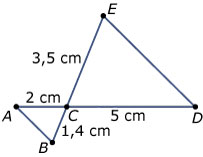 Hier zie je twee driehoeken, namelijk `Delta ABC` en `Delta CDE`.
Hier zie je twee driehoeken, namelijk `Delta ABC` en `Delta CDE`.
-
Met welk gelijkvormigheidskenmerk toon je aan dat beide gelijkvormig zijn? Je noteert dit wel zo: `Delta ABC ~ Delta DEC`.
-
Wat kun je op grond daarvan zeggen over de zijden `AB` en `DE`?
-
Neem aan, dat `|AB| = 1,8` cm. Hoe lang is dan `DE`?
-
Gegeven is een driehoek `ABC` en een punt `S` in de driehoek. `A'` ligt op het verlengde van `SA`, waarbij `|SA'| = 3|SA|`. Net zo ligt `B'` op het verlengde van `SB` met `|SB'| = 3|SB|`
en `C'` op het verlengde van `SC` met `|SC'| = 3|SC|`. Maak een tekening.
- Met welk kenmerk kun je aantonen dat `Delta SAB ~ Delta SA'B'`?
- Wat concludeer je over `|A'B'|`? Wat gaat natuurlijk net zo?
- Met welk kenmerk kun je aantonen dat `Delta ABC ~ Delta A'B'C'`?
- Hoe belangrijk is de factor 3 in het gegeven? Had die factor ook kleiner dan 1 mogen zijn?
- Formuleer op grond van het bovenstaande een stelling. Maak hem zo algemeen mogelijk.
- Geef in een tekening aan van welke hoeken je nu weet dat ze gelijk zijn.
Verwerken
-
Op een been van een hoek met hoekpunt `A` ligt een punt `B` en op het andere been ligt een punt `C`. `AB = 12` cm en `AC = 20` cm.
Op het verlengde van `BA` ligt een punt `D` met `AD = 5` cm en op het verlengde van `CA` ligt een punt `E` zo, dat `/_EDA = /_BCA`.
- Bereken de lengte van `AE`.
Op `AB` ligt een punt `F` met `AF = 5` cm en op `AC` ligt een punt `G` zo, dat `/_GFA = /_BCA`.
- Bereken de lengte van `AG`.
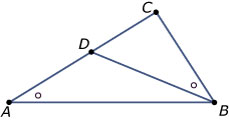 In de figuur hiernaast is `/_BAD = /_DBC`, `|AB| = 10`, `|AC| = 8` en `|BC| = 5`.
In de figuur hiernaast is `/_BAD = /_DBC`, `|AB| = 10`, `|AC| = 8` en `|BC| = 5`.
- Welke twee gelijkvormige driehoeken zijn er? Bewijs de gelijkvormigheid.
- Bereken de lengte van `DB`.
-
Teken in een willekeurige scherphoekige driehoek `ABC` een loodlijn `AD` vanuit `A` op zijde `BC` en een loodlijn `BE` vanuit `B` op zijde `AC`.
Het snijpunt van deze loodlijnen is `S`.
Bewijs dat `|AS| * |SD| = |BS| * |SE|`.
-
Vierhoek `ABCD` is een ruit.
De punten `P`, `Q`, `R` en `S` zijn de middens van de zijden van die ruit.
Bewijs dat `PQRS` een rechthoek is.
-
Bewijs dat je elke driehoek in vier gelijke delen kunt verdelen met behulp van drie middenparallellen.
-
In een driehoek `ABC` wordt op `AC` een punt `P_0` gekozen zo, dat `|AP_0| : |AC| = 1 : 5`.
Dan wordt vanuit `P_0` een lijn evenwijdig aan `BC` getrokken naar `P_1` op `AB` en vervolgens vanuit `P_1` een lijn evenwijdig aan `CA` naar `P_2` op `BC` en vanuit `P_2` een
lijn evenwijdig aan `AB` naar `P_3` op `CA`. Met `P_3` in plaats van `P_0` worden net zo weer drie lijnen getrokken, naar `P_4` op `AB`, `P_5` op `BC` en naar `P_6` op `CA`.
- Welk vermoeden levert een tekening over de ligging van `P_6`?
- Bewijs dat vermoeden (Aanwijzing: In welke verhouding verdelen de punten `P` de zijden van de driehoek?).
Testen
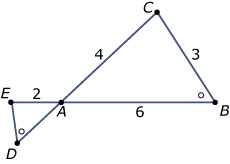 In de figuur hiernaast zie je twee lijnstukken `EB` en `DC` die elkaar snijden in `A`. Verder is gegeven `/_B = /_D`.
In de figuur hiernaast zie je twee lijnstukken `EB` en `DC` die elkaar snijden in `A`. Verder is gegeven `/_B = /_D`.
Bereken de lengte van `AD` en die van `ED`.
-
In driehoek `ABC` is `D` het midden van `BC` en `E` het midden van `AC`. De lijnstukken `BE` en `AD` snijden elkaar in `S`.
Bewijs dat `|AS| : |SD| = |BS| : |SE| = 2 : 1`.
 Hier zie je twee driehoeken, namelijk `Delta ABC` en `Delta CDE`.
Hier zie je twee driehoeken, namelijk `Delta ABC` en `Delta CDE`.





 In de figuur hiernaast is `/_BAD = /_DBC`, `|AB| = 10`, `|AC| = 8` en `|BC| = 5`.
In de figuur hiernaast is `/_BAD = /_DBC`, `|AB| = 10`, `|AC| = 8` en `|BC| = 5`.
 In de figuur hiernaast zie je twee lijnstukken `EB` en `DC` die elkaar snijden in `A`. Verder is gegeven `/_B = /_D`.
In de figuur hiernaast zie je twee lijnstukken `EB` en `DC` die elkaar snijden in `A`. Verder is gegeven `/_B = /_D`.