Bewijzen

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Bewijzen > Inleiding

Probeer de stelling bij Verkennen zelf te bewijzen. Bij de uitleg en de voorbeelden wordt er op terug gekomen.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Bewijzen > Uitleg

Opgaven

  1. In de Uitleg wordt een begin gemaakt met het bewijs van de stelling: Een driehoek waarvan de hoekpunten de middens zijn van drie zijden van een vierkant is rechthoekig en gelijkbenig.
    1. Laat zien dat de driehoeken `APR` en `DQR` congruent zijn.
    2. Leg uit hoe je daaruit het bewijs levert.

  2. In de Uitleg wordt de bewijsstructuur "Gegeven, te bewijzen, bewijs" ingeleid.
    1. Wat is het verschil tussen de stelling zelf en de beschrijving ervan onder de kopjes "Gegeven" en "Te bewijzen"?
    2. Wat is het belang van zo'n vaste bewijsstructuur?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Bewijzen > Theorie

Bekijk eerst de Theorie. Bekijk vervolgens de Voorbeelden, de volgende opgaven gaan daarover.

Opgaven

  1. In Voorbeeld 1 en Voorbeeld 2 zie je twee bewijzen van de stelling: Een driehoek waarvan de hoekpunten de middens zijn van drie zijden van een vierkant is rechthoekig en gelijkbenig.
    1. Hoe wordt in die bewijzen gebruik gemaakt van lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B?
    2. Loop beide bewijzen zelf na. Zorg ervoor dat je elke stap begrijpt.

  2. In Voorbeeld 3 vind je een bewijs van een stelling over het middelpunt van een cirkel door de drie hoekpunten van een driehoek.
    1. Hoe teken je de cirkel door de drie hoekpunten van een driehoek?
    Bekijk nu bij

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Bewijzen > GeoGebra

    hoe je het (gratis) computerprogramma GeoGebra kunt downloaden. In dit programma kun je de figuren die je bij een bewijs vaak wilt tekenen, gemakkelijk zelf construeren. Vaak kun je dan nog allerlei punten, lijnen en cirkels verplaatsen en bekijken wat daarvan het effect is.
    1. Construeer in GeoGebra nu een driehoek `ABC` en teken een cirkel door de drie hoekpunten. Bepaal het middelpunt `M` van die cirkel en bekijk wat er met `M` gebeurt als je de punten `A`, `B` en/of `C` verplaatst. (Zo maak je zelf de applet in het voorbeeld.)
    2. Kun je nog een andere vergelijkbare stelling formuleren en bewijzen?

  3. In Voorbeeld 4 zie je het bewijs van de kortste verbinding via een lijn tussen twee punten `A` en `B` die aan dezelfde kant van die lijn liggen (maar er niet op).
    Loop dit bewijs nog eens na, doe de constructie met GeoGebra. Vergelijk het met het bewijs dat je zelf eerder hebt geleverd in Meetkunde 1.2: Congruentie, opgave 12.

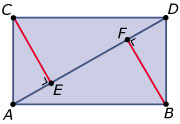  4. Gegeven is rechthoek `ABCD` met diagonaal `AC`. Bewijs dat de loodlijn uit punt `D` op `AC` gelijk is aan de loodlijn uit punt `B` op `AC`.
    1. Teken een geschikte figuur of construeer hem in GeoGebra. Teken beide loodlijnen er in, noem ze `DE` en `BF`.
    2. Welke lijnstukken in je figuur moeten nu gelijk zijn?
    3. Kun je geschikte congruente driehoeken vinden? Maak een plan voor je bewijs.
    4. Formuleer nu een volledig en duidelijk bewijs. Let goed op de verwijzingen naar de lijst van definities/stellingen in de Vlakke Meetkunde voor vwo wiskunde B.

Verwerken

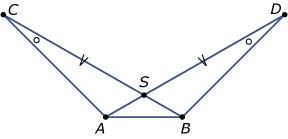  1. In de figuur zie je twee driehoeken `ABC` en `ABD` getekend.
    Verder is `CS = DS` en `/_C = /_D`.
    Bewijs dat `AS = BS`.

  2. Twee lijnstukken `AB` en `CD` zijn niet even lang en hebben een snijpunt `S` zo, dat `AS = SB` en `CS = SD`.
    Bewijs dat `AC` evenwijdig is aan `BD`.

  3. In `Delta ABC` is `AB = AC`. `D` is het midden van `AB`, `E` het midden van `AC`. Bewijs dat `BE = AD`.

  4. Op een lijn liggen, in deze volgorde, de punten `A`, `D`, `B` en `C`. `P` is een punt niet op die lijn. Verder is gegeven dat `/_APB = 2 * /_APD`.
    Bewijs dat `/_CPD = 1/2 * (/_CPB + /_CPA)`.

  5. In de figuur zie je twee driehoeken `ABC` en `AED` getekend.
    Verder is `AB = AD` en `AC = AE`.
    Bewijs dat `/_C = /_E`.

  6. Ga uit van een rechthoekige driehoek `ABC` met `/_A = 90`°. Op `BC` ligt punt `D` zo, dat `AD = AC`. Lijnstuk `DE` staat loodrecht op `AD` en punt `E` ligt op `AB`.
    Bewijs dat `ED = EB`.

  7. Op de zijden van `Delta ABC` zijn de gelijkzijdige driehoeken `CBD` en `ACE` getekend. Deze gelijkzijdige driehoeken overlappen `Delta ABC` niet.
    Bewijs dat `AD = BE`.

Testen

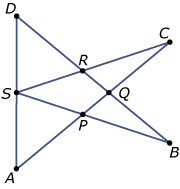  1. In de figuur hiernaast is gegeven `/_A = /_D`, `/_B = /_C` en punt `S` is het midden van lijnstuk `AD`.
    Bewijs dat `AC = BD`.

  2. Bewijs dat in een gelijkbenige driehoek de lijnstukken vanuit de hoeken tegenover de gelijke benen en loodrecht op die benen even lang zijn.