Congruentie

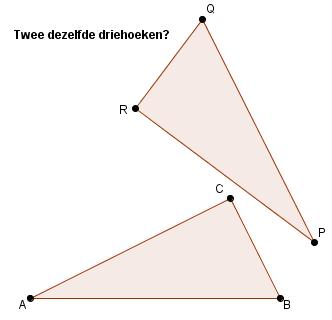
Inleiding

Bij het leveren van meetkundige bewijzen wil je vaak aantonen welke verschillende (delen van) figuren hetzelfde zijn. Figuren die qua vorm en afmeting gelijk zijn noem je congruent. Ze hebben dan dezelfde hoeken en afmetingen. Omdat veel figuren in driehoeken zijn te verdelen is het voor bewijzen belangrijk om te weten wanneer driehoeken congruent zijn.

Je leert nu:

werken met de congruentiekenmerken van driehoeken;
bewijzen leveren met behulp van congruente driehoeken;
de eigenschappen van bijzondere driehoeken gebruiken;
de driehoeksongelijkheid toepassen.

Je kunt al:

eenvoudige bewijzen leveren vanuit basisdefinities en axioma's van de meetkunde.

Verkennen

Er zijn precies vijf verschillende situaties waarin je een driehoek precies kunt tekenen en er ook maar ééntje mogelijk is.
Eén daarvan is ZZZ: de drie zijden zijn gegeven.

> Laat zien dat bij drie gegeven zijden er ook maar één driehoek is te tekenen door hem te construeren. Neem als lengtes van zijden |AB| = 6, |BC| = 3 en |AC| = 4.
> Lukt dit bij elke willekeurige set van drie getallen?

Een andere situatie is ZHZ: twee zijden en de hoek ertussen zijn gegeven.

> Laat ook nu zien dat er zo maar één driehoek te construeren is. Neem ∠A = 60°, |AB| = 6 en |AC| = 8.
> Bedenk zelf de andere drie situaties.
> Waarom is ZZH niet zo'n situatie?

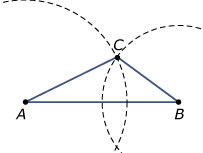
Uitleg

Als van een driehoek de drie zijden (b.v. |AB| = 6, |BC| = 3 en |AC| = 4) zijn gegeven, kun je hem construeren. Er zijn dan twee driehoeken ABC mogelijk.In de constructie kun je zien dat die qua vorm en afmetingen gelijk zijn. Het zijn congruente driehoeken. Als twee driehoeken gelijke zijden hebben zijn ze altijd congruent. Deze eigenschap van driehoeken heet een congruentiekenmerk.
De congruentiekenmerken voor driehoeken zijn:

drie gelijke zijden (ZZZ);
twee hoeken en de zijde ertussen (HZH);
twee zijden en de ingesloten hoek (ZHZ);
een zijde, een hoek op die zijde en de overstaande hoek (ZHH);
twee zijden en de rechte hoek tegenover één van die zijden (ZZR).

De drie letters gebruik je in bewijzen om het congruentiekenmerk weer te geven.
Ga zelf na, dat je in alle vijf gevallen precies één driehoek kunt construeren (of twee congruente). Met behulp van deze congruentiekenmerken kun je allerlei eigenschappen van bijzondere driehoeken bewijzen. Daarin geef je hoeken vaak aan met behulp van drie letters ∠ABC is de hoek met hoekpunt B en benen BA en BC.

‡

Opgaven

In de Uitleg zie je dat er vijf congruentie-kenmerken zijn. Bij elk ervan gaat het over drie hoeken en/of lijnen die twee driehoeken gelijk hebben.
1. Waarom is `HHH` geen congruentie-kenmerk?
2. ZZR is een congruentie-kenmerk, maar ZZH niet. Ga na waarom je niet een driehoek `ABC` vastlegt door te zeggen: `|AB| = 5` cm, `|AC| = 4` cm en `/_ABC = 45`°.

Je ziet in de Uitleg hoe je een driehoek construeert als de drie zijden zijn gegeven. Die constructie hoort bij congruentiekenmerk ZZZ.
Geef een voorbeeld van een constructie die hoort bij `HZH`. Beschrijf mogelijke gegevens en voer de constructie uit.

Theorie

Twee driehoeken zijn congruent als ze gelijk hebben:

drie zijden (ZZZ);
twee hoeken en de zijde ertussen (HZH);
twee zijden en de ingesloten hoek (ZHZ);
een zijde, een hoek op die zijde en de overstaande hoek (ZHH);
twee zijden en de rechte hoek tegenover één van die zijden (ZZR).

Je noemt dit de congruentiekenmerken van driehoeken. Met behulp van congruentie kun je allerlei eigenschappen van (bijzondere) driehoeken bewijzen. Bijvoorbeeld:

In elke rechthoekige driehoek (een driehoek met een rechte hoek) geldt de stelling van Pythagoras. Dus als de rechthoekszijden lengtes van a en b hebben en de hypothenusa (schuine zijde) heeft lengte c, dan is a² + b² = c².
Als in een driehoek de stelling van Pythagoras geldt is het een rechthoekige driehoek.
In elke gelijkbenige driehoek (een driehoek met twee gelijke zijden) zijn de hoeken tegenover de even lange zijden even groot.
In elke gelijkzijdige driehoek (een driehoek met drie gelijke zijden) zijn alle hoeken even groot.

Tenslotte is bij driehoeken nog van belang dat elke zijde van een driehoek altijd kleiner is dan de som van de twee andere. Dit heet de driehoeksongelijkheid: voor drie punten A, B en C die niet op één lijn liggen geldt: |AB| + |BC| > |AC|.

‡

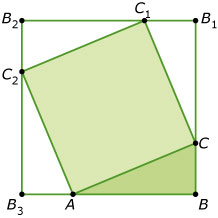
Voorbeeld 1

Hier zie je een figuur waarmee je de stelling van Pythagoras bewijst in de rechthoekige driehoek ABC. Eerst wordt een vierkant op zijde AC geconstrueerd. Daarna wordt de driehoek om P (het snijpunt van de diagonalen van het vierkant) over 90° gedraaid. Zo ontstaan vier congruente rechthoekige driehoeken.
Belangrijk is dat vanwege de congruentie van de vier driehoeken bij de punten C, C₁, C₂ en A gestrekte hoeken ontstaan.
Dit komt omdat congruente driehoeken gelijke hoeken hebben en dus:
∠BCA + 90° + ∠C₁AB₁ =
= ∠BCA + 90° + ∠CAB = 180°.

Nu weet je zeker dat BB₁B₂B₃ een vierkant is met zijden van a + b.
Verder is CC₁C₂A een vierkant met zijden c.
En tenslotte heeft elk van de vier rechthoekige driehoeken een oppervlakte van $\frac{1}{2}$ ab.

Ga nu zelf na dat uit (a + b)² = 4 · $\frac{1}{2}$ ab + c² volgt dat a² + b² = c².

‡

Voorbeeld 2

In ΔABC geldt de stelling van Pythagoras: a² + b² = c².
Bewijs nu dat deze driehoek rechthoekig is.

Antwoord

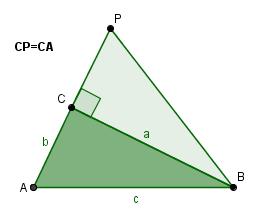
Construeer op ΔABC een rechthoekige driehoek CBP waarvan ∠BCP = 90° en bovendien |CP| = |CA| = b.
In ΔCBP geldt de stelling van Pythagoras: |CB|² + |CP|² = |BP|².
En dus is |BP|² = b² + a² = c² en |BP| = |AB|.

Daarom zijn de twee driehoeken ABC en PBC congruent (ZZZ).
En dus is ∠ACB = ∠BCP = 90°.

‡

Voorbeeld 3

ΔABC is gelijkbenig want heeft twee gelijke zijden AC en BC.
Bewijs nu dat hij twee gelijke hoeken heeft.

Antwoord

Teken de loodlijn CD op AB.
Bekijk de twee driehoeken ADC en BDC.
Hiervan is: |AC| = |BC|, |CD| = |CD| en ∠BDC = ∠ADC = 90°.
En dus is ΔADC congruent met ΔBDC (ZZR).
En daarom is ∠A = ∠B.

Je kunt dit ook bewijzen door aan te tonen dat ΔABC congruent is met ΔBAC (ZZZ).
Bedenk zelf hoe dan het bewijs precies verloopt.

‡

Voorbeeld 4

ΔABC is gelijkzijdig want heeft drie gelijke zijden.
Bewijs nu dat hij drie gelijke hoeken van 60° heeft.

Antwoord

In het bewijs wordt gebruik gemaakt van voorgaande stellingen.
Bijvoorbeeld dat de som van de hoeken van een driehoek 180° is.
En van de stelling dat in een gelijkbenige driehoek de hoeken tegenover de even lange zijden even groot zijn. Nu merk je hoe handig een goed systeem van verwijzen naar al eerder bewezen stellingen en de axioma's is. Daarvoor ga je straks de lijst van definities en stellingen in de vlakke meetkunde van vwo_b gebruiken.

Omdat |AB| = |AC| is ∠ABC = ∠ACB.
Omdat |AB| = |BC| is ∠BAC = ∠ACB.
Dus zijn alle drie de hoeken van de driehoek gelijk.
En dus zijn ze elk 180°/3 = 60°.

‡

Opgaven

In Voorbeeld 1 wordt een bewijs voor de stelling van Pythagoras geleverd.
1. Waarom moet worden aangetoond dat `BB_1B_2B_3` een vierkant is?
2. Ga de laatste regel van het bewijs ook inderdaad zelf na.

In Voorbeeld 2 wordt de omgekeerde stelling van Pythagoras bewezen.
1. Teken een geschikte figuur om het bewijs te verduidelijken. Van welk congruentiekenmerk wordt gebruik gemaakt?
2. Bewijs dat een driehoek met zijden van 16, 30 en 34 cm rechthoekig is.

Bekijk in Voorbeeld 3 het bewijs dat een gelijkbenige driehoek twee gelijke hoeken heeft.
In het antwoord staat een tweede manier beschreven om dit bewijs te leveren. Schrijf op hoe dit tweede bewijs verloopt.

In Voorbeeld 4 zie je hoe je kunt bewijzen dat de hoeken van een gelijkzijdige driehoek allemaal gelijk zijn aan 60°. Je gebruikt er eerder bewezen stellingen bij.
Bewijs nu zelf: Elke gelijkbenige rechthoekige driehoek heeft twee hoeken van 45°.
Gebruik hierbij alleen stellingen die horen bij de lijst van definities en stellingen die je voor het vwo-examen wiskunde B moet kennen.

Bewijs met behulp van congruentie de stelling: Als in een driehoek twee hoeken gelijk zijn, dan is die driehoek gelijkbenig.

De afstand van een punt `P` tot een lijn `l` is de lengte van het kortste verbindingslijnstuk van `P` en een punt `Q` op die lijn `l`.
Bewijs met behulp van de stelling van Pythagoras dat dit kortste verbindingslijnstuk `PQ` een rechte hoek met lijn `l` maakt.

Gegeven is `Delta ABC` met `/_A > /_B`. Je wilt bewijzen dat tegenover de grootste hoek ook de langste zijde zit, dus `|BC| > |AC|`.
1. Teken een geschikte figuur. Teken op `BC` een punt `D`, zo, dat `/_BAD = /_ABD`.
2. Waarom is `|AD| = |BD|`?
3. Pas de driehoeksongelijkheid toe in `Delta ADC` en toon hiermee aan dat `|BC| > |AC|`.

Verwerken

In een vierkant `ABCD` zijn de twee diagonalen `AC` en `BD` getrokken. Hun snijpunt is `S`.
1. Bewijs dat de driehoeken `ABD` en `ABC` congruent zijn.
2. Bewijs dat de driehoeken `ABS` en `CDS` congruent zijn.
3. Bewijs dat `S` het midden is van `AC` en van `BD`.

Een driehoek heeft een zijde van 8 cm en en zijde van 5 cm.
1. Kan de derde zijde 13 cm zijn? Wat kun je zeggen over de lengte van de derde zijde?
Een andere driehoek heeft een zijde met een lengte van 1 m.
1. Wat kun je zeggen over de som van de lengtes van de andere zijden? En over hun verschil?

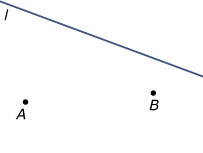Je wilt de kortste weg van `A` naar `B` via een punt op lijn `l` tekenen.
1. Teken die kortste weg.
2. Bewijs dat dit inderdaad de kortste weg is. Gebruik de driehoeksongelijkheid.

Bewijs dat de omtrek van een vierhoek groter is dan de som van de lengten van de diagonalen.

Definitie: “de afstand tussen twee evenwijdige lijnen is de lengte van een loodlijn die je vanuit een punt op de éne lijn op de andere lijn neerlaat”. Daar is nog wel wat op aan te merken. Maakt het niets uit waar je dat punt kiest? Maakt het niets uit op welk van de twee lijnen je dat punt kiest? En is dat dan echt de kortste afstand van alle lijnstukjes tussen de twee lijnen?
Noem de lijnen `l` en `m`.
1. Bewijs: als `P` een punt op `l` is en `PQ` de loodlijn vanuit `P` op `m`, dan is `QP` de loodlijn vanuit `Q` op `l`.
2. Bewijs: als `P'` een (ander) punt is op `l` en `P'Q'` de loodlijn vanuit `P'` op `m`, dan zijn `PQ` en `P'Q'` even lang (gebruik een hulplijn).
3. Waarom kun je nu de definitie goedkeuren?
4. Is de zo gedefinieerde afstand tussen twee evenwijdige lijnen ook de kleinst mogelijke afstand tussen een punt op de ene en een punt op de andere lijn? Geef een bewijs. (Gebruik de stelling van Pythagoras.)

In opgave 9 is bewezen dat in een driehoek de grootste hoek altijd tegenover de langste zijde zit. Geldt ook dat de langste zijde altijd tegenover de grootste hoek zit? Onderzoek dit en geef een bewijs of een tegenvoorbeeld.

Testen

Van `Delta ABC` is gegeven: `|AC| = |BC|`. `D` is het midden van `AC` en `E` is het midden van `BC`.
Bewijs dat de loodlijnen vanuit `D` en vanuit `E` op `AB` even lang zijn.

Van de vierhoek `ABCD` is gegeven: `|AB| = |CD|`, `|AD| = |BC|` en `/_ABC = 90`°.
1. Laat met een hulplijn zien: de vier hoeken zijn samen 360°.
2. Bewijs dat `/_ADC = 90`°.
3. Bewijs dat `/_BAD = /_BCD = 90`°.
4. Bewijs dat de twee diagonalen even lang zijn.
5. Bewijs dat `/_BAC = /_ABD = /_ACD = /_BDC`.
6. Bewijs dat de diagonalen elkaar doormidden delen.

In een rechthoekige driehoek (de rechte hoek bij `A`) is `D` een punt op `BC` zo, dat `/_DAB = /_DBA`. (Maak zelf een tekening).
1. Laat zien dat `/_ACB = 90^(text(o)) - /_CBA`.
2. Laat zien dat `Delta DCA` gelijkbenig is.
3. Bewijs dat `|AD| = |DB| = |CD|`.