Congruentie

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Congruentie > Inleiding

Probeer de vraag bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Congruentie > Uitleg

Opgaven

  1. In de Uitleg zie je dat er vijf congruentie-kenmerken zijn. Bij elk ervan gaat het over drie hoeken en/of lijnen die twee driehoeken gelijk hebben.
    1. Waarom is `HHH` geen congruentie-kenmerk?
    2. ZZR is een congruentie-kenmerk, maar ZZH niet. Ga na waarom je niet een driehoek `ABC` vastlegt door te zeggen: `|AB| = 5` cm, `|AC| = 4` cm en `/_ABC = 45`°.

  2. Je ziet in de Uitleg hoe je een driehoek construeert als de drie zijden zijn gegeven. Die constructie hoort bij congruentiekenmerk ZZZ.
    Geef een voorbeeld van een constructie die hoort bij `HZH`. Beschrijf mogelijke gegevens en voer de constructie uit.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Congruentie > Theorie

Bekijk eerst de Theorie. Bekijk vervolgens de Voorbeelden, de volgende opgaven gaan daarover.

Opgaven

  1. In Voorbeeld 1 wordt een bewijs voor de stelling van Pythagoras geleverd.
    1. Waarom moet worden aangetoond dat `BB_1B_2B_3` een vierkant is?
    2. Ga de laatste regel van het bewijs ook inderdaad zelf na.

  2. In Voorbeeld 2 wordt de omgekeerde stelling van Pythagoras bewezen.
    1. Van welk congruentiekenmerk wordt gebruik gemaakt?
    2. Bewijs dat een driehoek met zijden van 16, 30 en 34 cm rechthoekig is.

  3. Bekijk in Voorbeeld 3 het bewijs dat een gelijkbenige driehoek twee gelijke hoeken heeft.
    In het antwoord staat een tweede manier beschreven om dit bewijs te leveren. Schrijf op hoe dit tweede bewijs verloopt.

  4. In Voorbeeld 4 zie je hoe je kunt bewijzen dat de hoeken van een gelijkzijdige driehoek allemaal gelijk zijn aan 60°. Je gebruikt er eerder bewezen stellingen bij.
    Bewijs nu zelf: Elke gelijkbenige rechthoekige driehoek heeft twee hoeken van 45°.
    Gebruik hierbij alleen stellingen die horen bij de lijst van definities en stellingen die je voor het vwo-examen wiskunde B moet kennen.

  5. Bewijs met behulp van congruentie de stelling: Als in een driehoek twee hoeken gelijk zijn, dan is die driehoek gelijkbenig.

  6. De afstand van een punt `P` tot een lijn `l` is de lengte van het kortste verbindingslijnstuk van `P` en een punt `Q` op die lijn `l`.
    Bewijs met behulp van de stelling van Pythagoras dat dit kortste verbindingslijnstuk `PQ` een rechte hoek met lijn `l` maakt.

  7. Gegeven is `Delta ABC` met `/_A > /_B`. Je wilt bewijzen dat tegenover de grootste hoek ook de langste zijde zit, dus `|BC| > |AC|`.
    1. Teken een geschikte figuur. Teken op `BC` een punt `D`, zo, dat `/_BAD = /_ABD`.
    2. Waarom is `|AD| = |BD|`?
    3. Pas de driehoeksongelijkheid toe in `Delta ADC` en toon hiermee aan dat `|BC| > |AC|`.

Verwerken

  1. In een vierkant `ABCD` zijn de twee diagonalen `AC` en `BD` getrokken. Hun snijpunt is `S`.
    1. Bewijs dat de driehoeken `ABD` en `ABC` congruent zijn.
    2. Bewijs dat de driehoeken `ABS` en `CDS` congruent zijn.
    3. Bewijs dat `S` het midden is van `AC` en van `BD`.

  2. Een driehoek heeft een zijde van 8 cm en en zijde van 5 cm.
    1. Kan de derde zijde 13 cm zijn? Wat kun je zeggen over de lengte van de derde zijde?
    Een andere driehoek heeft een zijde met een lengte van 1 m.
    1. Wat kun je zeggen over de som van de lengtes van de andere zijden? En over hun verschil?

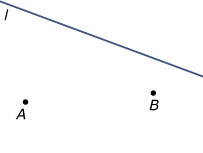  3. Je wilt de kortste weg van `A` naar `B` via een punt op lijn `l` tekenen.
    1. Teken die kortste weg.
    2. Bewijs dat dit inderdaad de kortste weg is. Gebruik de driehoeksongelijkheid.

  4. Bewijs dat de omtrek van een vierhoek groter is dan de som van de lengten van de diagonalen.

  5. Definitie: “de afstand tussen twee evenwijdige lijnen is de lengte van een loodlijn die je vanuit een punt op de éne lijn op de andere lijn neerlaat”. Daar is nog wel wat op aan te merken. Maakt het niets uit waar je dat punt kiest? Maakt het niets uit op welk van de twee lijnen je dat punt kiest? En is dat dan echt de kortste afstand van alle lijnstukjes tussen de twee lijnen?
    Noem de lijnen `l` en `m`.
    1. Bewijs: als `P` een punt op `l` is en `PQ` de loodlijn vanuit `P` op `m`, dan is `QP` de loodlijn vanuit `Q` op `l`.
    2. Bewijs: als `P'` een (ander) punt is op `l` en `P'Q'` de loodlijn vanuit `P'` op `m`, dan zijn `PQ` en `P'Q'` even lang (gebruik een hulplijn).
    3. Waarom kun je nu de definitie goedkeuren?
    4. Is de zo gedefinieerde afstand tussen twee evenwijdige lijnen ook de kleinst mogelijke afstand tussen een punt op de ene en een punt op de andere lijn? Geef een bewijs. (Gebruik de stelling van Pythagoras.)

  6. In opgave 9 is bewezen dat in een driehoek de grootste hoek altijd tegenover de langste zijde zit. Geldt ook dat de langste zijde altijd tegenover de grootste hoek zit? Onderzoek dit en geef een bewijs of een tegenvoorbeeld.

Testen

  1. Van `Delta ABC` is gegeven: `|AC| = |BC|`. `D` is het midden van `AC` en `E` is het midden van `BC`.
    Bewijs dat de loodlijnen vanuit `D` en vanuit `E` op `AB` even lang zijn.

  2. Van de vierhoek `ABCD` is gegeven: `|AB| = |CD|`, `|AD| = |BC|` en `/_ABC = 90`°.
    1. Laat met een hulplijn zien: de vier hoeken zijn samen 360°.
    2. Bewijs dat `/_ADC = 90`°.
    3. Bewijs dat `/_BAD = /_BCD = 90`°.
    4. Bewijs dat de twee diagonalen even lang zijn.
    5. Bewijs dat `/_BAC = /_ABD = /_ACD = /_BDC`.
    6. Bewijs dat de diagonalen elkaar doormidden delen.

  3. In een rechthoekige driehoek (de rechte hoek bij `A`) is `D` een punt op `BC` zo, dat `/_DAB = /_DBA`. (Maak zelf een tekening).
    1. Laat zien dat `/_ACB = 90^(text(o)) - /_CBA`.
    2. Laat zien dat `Delta DCA` gelijkbenig is.
    3. Bewijs dat `|AD| = |DB| = |CD|`.