Congruentie

Antwoorden bij de opgaven

    1. Als twee hoeken gelijk zijn dan is de derde hoek automatisch gelijk. Er zijn dan maar twee gegevens bekend van de driehoek, de lengtes van de zijden kunnen nog variëren.
    2. Bij ZZH heb je nog twee mogelijkheden: een scherphoekige driehoek of een stomphoekige. Teken `AB = 5` en `/_B = 45`°. Teken nu de cirkel met middelpunt `A` en straal `AC = 4`. Deze cirkel snijdt het tweede been van `/_B` twee keer. Er zijn dus twee punten `C` mogelijk.
  2. Neem bijvoorbeeld `AB = 5` cm en `/_A = 40`° en `/_B = 60`°. Deze hoeken hebben behalve `AB` nog een ander been. Die andere benen snijden elkaar in `C` en zo krijg je `Delta ABC`. Voorwaarde is wel dat `/_A + /_B < 180`°.
    1. Omdat het niet een gegeven is en anders de oppervlakte ervan geen `(a + b)^2` is.
    2. Uit `(a + b)^2 = 4 * 1/2 ab + c^2` volgt door haakjes uitwerken: `a^2 + 2ab + b^2 = 2ab = c^2` en dus `a^2 + b^2 = c^2`.
    1. ZZZ, je weet immers nog niet of `/_ACB` recht is, dus van gelijke hoeken mag je geen gebruik maken.
    2. Ga na dat `16^2 + 30^2 = 34^2`. Dus geldt in de gegeven driehoek de SvP en daarom is hij rechthoekig (omgekeerde stelling van Pythagoras).
  5. Uit `|AB| = |BA|`, `|AC| = |BC|` en `|BC| = |AC|` volgt dat `Delta ABC` congruent is met `Delta BAC` (ZZZ).
    En dus is `/_A = /_B`.
  6. Gegeven: Een gelijkbenige rechthoekige driehoek `ABC` met `/_C = 90`° en `AC = BC`.
    Omdat `Delta ABC` gelijkbenig is zijn de hoeken tegenover de gelijke benen even groot, dus `/_A = /_B` (gelijkbenige driehoek).
    Omdat de hoeken van een driehoek samen 180° zijn (hoekensom driehoek) en `/_C = 90`° is `/_A + /_B = 90`°, zodat ze elk 45° zijn.
    (Opmerking: Dit bewijs is nogal overbodig omdat de stelling zelf al in de lijst van gegeven stellingen en definities voorkomt. Maar het is wel een goede oefening. Bovendien zie je zo dat veel van de stellingen die in die lijst voorkomen weer uit andere stellingen van diezelfde lijst zijn af te leiden. Het maakt duidelijk dat de lijst maar een vrij willekeurige greep is uit het geheel aan bewezen stellingen in de vlakke meetkunde.)
  7. Gegeven: `Delta ABC` met `/_A = /_B`.
    Teken nu de loodlijn `CD` vanuit `C` op `AB`. Omdat `/_A = /_B` en `/_D_1 = /_D_2 = 90`° en `|CD| = |CD|` zijn de driehoeken `ADC` en `BDC` congruent (ZHH). En daaruit volgt `|AC| = |BC|`.
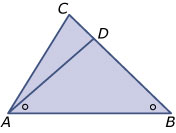
  8. Stel dat dit niet zo zou zijn en dat `PQ` de kortste verbindingslijn van `P` met een punt `Q` op `l` is. Er is dan een driehoek `PP'Q` te tekenen waarin `PP' _|_ l`. In die driehoek is `PQ^2 = PP'^2 + P'Q^2` (Pythagoras) en dus `|PQ| > |PP'|`. Dat is in tegenspraak met het feit dat `|PQ|` de korste verbindingslijn van `P` met een punt op `l` zou zijn.
    1. Zie figuur.
    2. Omdat `/_BAD = /_ABD` is `Delta ABD` gelijkbenig.
    3. Vanweg de driehoeksongelijkheid is `|AC| < |AD| + |DC| = |BD| + |DC| = |BC|`.
    1. `|AB| = |BA|`, `|AD| = |BC|` en `/_A = /_B = 90`° zijn de driehoeken `ABD` en `ABC` congruent (ZHZ).
    2. `ABCD` is een ruit die tevens rechthoek is (vierkant). In de ruit delen de diagonalen de hoeken middendoor (ruit).
      Dus zijn van `Delta ABS` de hoeken op `AB` beide 45°. Voor `Delta CDS` zijn op dezelfde manier de twee hoeken op `CD` beide 45°.
      Omdat ook `|AB| = |CD|` zijn `Delta ABS` en `Delta CDS` congruent (HZH).
    3. Omdat `Delta ABS` en `Delta CDS` congruent zijn is `|AS| = |CS|` en `|BS| = |DS|`.
    1. De lengte van de derde zijde moet inliggen tussen 3 en 13 cm.
    2. De som van de lengtes van de ander twee zijden moet meer dan 1 m zijn. Het verschil is kleiner dan 1 m.
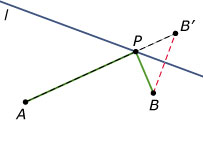  12. Teken `B'` zo, dat `BB'` loodrecht `l` en `|BS| = |SB'|` als `S` het snijpunt van `BB'` met `l` is.
    Vanwege de driehoeksongelijkheid is de rechte lijn `AB'` de korste verbinding tussen `A` en `B'`.
    Vanwege de congruentie van de driehoeken `BSP` en `B'SP` (ZHZ) is `|AP| + |PB| = |AP| + |PB'|` dus ook de kortste verbinding van `A` naar `B` via `l`.
  13. Gegeven: Vierhoek `ABCD`, het snijpunt van de diagonalen is `S`.
    Te bewijzen: `|AB| + |BC| + |CD| + |DA| > |AC| + |BD|`.
    Bewijs: `|AB| + |BC| > |AC|` en `|AD| + |DC| > |AC|`. Optellen geeft: `|AB| + |BC| + |AD| + |DC| > 2 * |AC|` (1).
    `|AD| + |AB| > |BD|` en `|BC| + |CD| > |BD|`. Optellen geeft: `|AB| + |AD| + |BC| + |DC| > 2 * |BD|` (2).
    (1)en (2) optellen geeft: `2 * (|AB| + |BC| + |AD| + |DC|) > 2 * (|AC| + |BD|)`.
    Dus `|AB| + |BC| + |CD| + |DA| > |AC| + |BD|`.
  14. Gegeven: `/_A` is een stompe hoek in `Delta ABC`.
    Te bewijzen: `/_B` en `/_C` zijn scherp.
    Bewijs: Neem aan dat `/_B` niet scherp is, dan is de som `/_A + /_B + /_C` meer dan 180°. Neem aan dat `/_C` niet scherp is, dan is de som `/_A + /_B + /_C` meer dan 180°. Dit leidt in beide gevallen tot een tegenspraak, dus `/_B` en `/_C` zijn beide scherp.
    1. Gegeven: `P` ligt op `l`. `PQ` is de loodlijn vanuit `P` op `m`.
      Te bewijzen: `QP` is de loodlijn vanuit `Q` op `l`.
      Bewijs: De lijnen `l` en `m` zijn evenwijdige lijnen gesneden door `PQ`. F-hoeken zijn gelijk, dus `/_Q = 90`° betekent dat ook `/_P = 90`°.
    2. Bewijs: `PQ` en `P'Q` zijn beide loodrecht op `m`. Dus `PQ` evenwijdig met `P’Q’`. Omdat `/_P = 90`° is `/_P' = 90`° en dus is `PQQ’P’` een rechthoek, zodat `|PQ| = |P’Q’|`.
    3. Geldt voor alle punten `P` en `Q` op twee evenwijdige lijnen.
    4. Ja. Bewijs: Neem punt `R` ongelijk aan `Q` op `m`. Neem aan dat `|PR| < |PQ|`. Dan is `Delta PQR` een rechthoekige driehoek. Hierin geldt: `|PQ|^2 + |QR|^2 = |PR|^2` zodat `|PR| > |PQ|`. Dit is in tegenspraak met het gestelde.
  16. Gegeven: `Delta ABC` met `|BC| > |AC|`.
    Te bewijzen: `/_A > /_B`.
    Bewijs: Neem aan dat `/_A < /_B`, dan kies je `D` op `AC` zodat `/_DAB = /_DBA`. Dan is `|CB| < |DC| + |DB| = |DC| + |DA| = |AC|`. Tegenspraak. Het gestelde is niet waar.
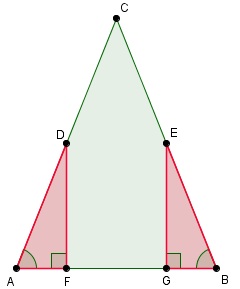  17. Gegeven: `Delta ABC` met `|AC| = |BC|` en `D` is het midden van `AC`, `E` is het midden van `BC`. `DF` en `EG` zijn loodlijnen op `AB`.
    Te bewijzen: `|DF| = |EG|`.
    Bewijs: Omdat `|AC| = |BC|` is `/_A = /_B` (gelijkbenige driehoek). Verder is `|AD| = 1/2 * |AC| = 1/2 * |BC| = |BE|`. En tenslotte is `/_F = /_G = 90`°. Dus is `Delta AFD ~= Delta GBE` (het teken `~=` betekent congruent, je gebruikt ZHH). En daarom is `|DF| = |EG|`.
    1. Trek bijvoorbeeld diagonaal `AC`. Je hebt dan twee driehoeken waarvan de hoekensom 180&de; is: `/_A_1 + /_B + /_C_1 = 180`° en `/_A_2 + /_D + /_C_2 = 180`°. En dus is `/_A_1 + /_B + /_C_1 + /_A_2 + /_D + /_C_2 = /_A + /_B + /_C + /_D = 360`°.
    2. Volgt uit de congruentie (ZZZ) van de driehoeken `ABC` en `CDA`.
    3. Uit de congruentie van de driehoeken `ABC` en `CDA` volgt dat `AB` evenwijdig is met `CD` (Z-hoeken).
    4. Volgt uit de congruentie (ZHZ) van de driehoeken `ABC` en `DCB`.
    5. Volgt uit de evenwijdigheid van `AB` en `CD`.
    6. Volgt uit de congruentie (HZH) van de driehoeken `ABS` en `DCS`.
    1. `Delta ABC` is rechthoekig, dus `/_ACB + /_CBA = 90`°, of `/_ACB = 90^(text(o)) - /_CBA`.
    2. `/_CAD = 90^(text(o)) - /_BAD = 90^(text(o)) - /_CBA = /_ACB`.
    3. Uit de gelijkbenigheid van `Delta ABD` volgt `|BD| = |AD|`.
      Uit de gelijkbenigheid van `Delta ADC` volgt `|CD| = |AD|`.
      Dus `|AD| = |BD| = |CD|`.