Basisbegrippen

Inleiding

De Griek Euclides (ongeveer 300 v.Chr.) was de eerste die een wiskundige theorie opbouwde. Hij legde de grondbegrippen van de theorie vast in definities, hij ging uit van een klein aantal aannames die hij proposities of axioma's noemde, en verder gebruikte hij enkele algemene aannamen. Die theorie verwoordde hij in zijn boek "Stoicheia" ofwel "De Elementen" het beroemdste wiskundeboek aller tijden. Hij poogde er een fundament mee te leggen voor alle wiskunde, ook getallen behandelde hij als lijnstukken omdat de hele theorie op meetkundige inzichten was gestoeld. Alle wiskunde van die tijd leidde hij uit zijn definities en axioma's af door logische redeneringen, die bewijzen worden genoemd.

Je leert nu:

• de begrippen definitie, axioma, vermoeden en bewijs;
• (eenvoudige) bewijzen leveren vanuit de basisdefinities en axioma's;
• het begrip bewijs uit het ongerijmde.

Je kunt al:

• verstandig redeneren.

Verkennen

Je weet wel dat de som van de hoeken van een driehoek 180° is.
> Maar kun je dat ook bewijzen?

Uitleg

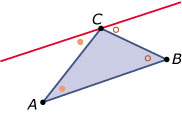
Vaak wordt het bewijs als volgt geleverd:

• Trek door C een lijn evenwijdig aan AB.
• Bij C vind je dan drie hoeken die samen een gestrekte hoek vormen: een hoek die (Z-hoeken) gelijk is aan ∠A, hoek C en een hoek die (Z-hoeken) gelijk is aan ∠B.
• Een gestrekte hoek is 180° dus de hoeken A, B en C zijn samen 180°.

Maar dit "bewijs" rammelt nogal. Wat zijn Z-hoeken? Waarom/wanneer zijn die gelijk? En hoe zit het met een gestrekte hoek? Er worden begrippen gebruikt die kennelijk al eerder zijn aangeleerd. En zijn die dan op hun beurt ook goed vastgelegd en zijn hun eigenschappen eerst bewezen?
Voor een goed bewijs moet dat in ieder geval zeker zijn.
Voor een goed bewijs heb je dus nodig:

• goede afspraken over de betekenis van alle begrippen: goede definities;
• een aantal goed omschreven uitgangspunten: goede axioma's;
• goede logische redeneerregels die iedereen hanteert.

‡

Opgaven

1. Bekijk de Uitleg. Je ziet er een redenering waaruit blijkt dat de som van de hoeken van een driehoek 180° is.
   1. Laat zien dat deze redenering ook geldt als punt `C` veel verder naar rechts ligt.
   2. Wat zijn Z-hoeken precies? Waarom is de evenwijdigheid van de lijn door `C` met `AB` belangrijk?
   Toen in West-Europa landen ontstonden met eigen regeringen en ambtenaren, werd het bepalen van de grootte van het grondgebied belangrijk. Landmeters gebruikten daarbij driehoeksmeting. Ze werken dan met driehoeken. En ook zij namen aan dat de som van de hoeken van een driehoek 180° is.
   2. Kun je laten zien dat dit voor driehoeken op het aardoppervlak niet waar kan zijn? Waarom ontdekten de landmeters dat niet meteen?


2. Je kent natuurlijk de stelling van Pythagoras wel. Zoek een bewijs van die stelling op, bijvoorbeeld via internet.
   Probeer dat bewijs zo te formuleren dat je het zelf goed begrijpt. Schrijf een aantal aannames op die in dit bewijs worden gedaan.
   


3. In de Oudheid werden voor constructies alleen liniaal en passer gebruikt.
   Je krijgt een potlood, een (grote) passer, een liniaal en een vel A4. Bijna aan de bovenrand van het papier is een lijnstuk getekend, bijna even lang als de bovenrand. De passerpunt mag niet buiten het papier worden gezet.
   1. Hoe kun je dat lijnstuk in vier gelijke delen verdelen?
   2. Hoe kun je, ergens op het papier, een hoek van 45° maken?
   3. Hoe kun je, ergens op het papier, een hoek van 60° maken? En een van 30°?


4. Je krijgt een potlood, een (grote) passer, een liniaal zonder maatverdeling en een vel papier waarop drie lijnstukken zijn getekend.
   Hoe kun je een driehoek tekenen met de drie lijnstukken als zijden? Lukt dat altijd? Wanneer wel en wanneer niet? Als het wel lukt, kun je dan maar één driehoek tekenen of zijn er meer oplossingen mogelijk?

Theorie

Een wiskundige theorie bestaat uit

• Een aantal definities van begrippen.
• Een zo klein mogelijk aantal basisaannames, ook wel axioma's genoemd.
• De stellingen, dat wil zeggen beweringen die door middel van logisch redeneren kunnen worden afgeleid uit de axioma's. Zo'n logische redenering heet het bewijs van de stelling.

Ook de vlakke meetkunde kent zo'n theorieopbouw die al meer dan 2200 jaar geleden is gestart met de Griek Euclides.
In de vlakke meetkunde heb je

• de begrippen punt, lijn, lijnstuk en hoek die voor iedereen duidelijk worden verondersteld;
• een lijst met definities van begrippen;
• precies vijf axioma's.

Basisdefinities en basisbegrippen

De begrippen punt, lijn, lijnstuk en hoek worden bekend verondersteld.

• De afstand tussen twee punten A en B is de lengte van het lijnstuk AB, genoteerd als |AB|, als AB of als d(A,B) (de d van distance).
• Een cirkel bestaat uit alle punten op een bepaalde afstand van een vast punt, zijn middelpunt.
• Een halve lijn is het deel van een lijn aan één kant van een punt op die lijn, inclusief dat punt (de benen van een hoek zijn halve lijnen).
• Het verlengde van een lijnstuk AB is de halve lijn van de lijn door A en B die in B begint en waar A niet op ligt (het verlengde van BA is een andere halve lijn).
• Een gestrekte hoek is een hoek waarvan de benen in elkaars verlengde liggen.
• Een rechte hoek (90°) is de helft van een gestrekte hoek (180°).
• Twee hoeken die samen een gestrekte hoek vormen zijn elkaars nevenhoek.
• Een driehoek bestaat uit drie punten, niet op één lijn (de hoekpunten) en de drie lijnstukken tussen die punten (de zijden). Telkens tussen twee zijden liggen de drie hoeken van de driehoek. Je duidt een driehoek aan met zijn hoekpunten: ΔABC.
• Twee lijnen snijden elkaar als ze één punt gemeenschappelijk hebben, het sijpunt.
• Twee lijnen heten evenwijdig als ze elkaar niet snijden (d.w.z. geen punt gemeen hebben).
• De loodlijn uit een punt P op een lijn l is de lijn door P die een rechte hoek maakt met l (loodrecht staat op l). Het snijpunt van l en de loodlijn S is het voetpunt van de loodlijn.
• De middelloodlijn van een lijnstuk AB is de lijn die AB loodrecht middendoor snijdt.

De vijf axioma's

Dit zijn de befaamde vijf axioma's (aannames) van de Euclidische vlakke meetkunde.

1. Door twee punten gaat precies één lijn.
2. Twee niet evenwijdige lijnen snijden elkaar in precies één punt.
3. Door een punt niet op een lijn l gaat precies één lijn evenwijdig met l.
4. Door een punt niet op een lijn l gaat precies één lijn die l loodrecht snijdt.

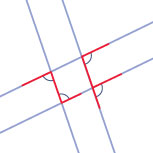
5. Als twee evenwijdige lijnen worden gesneden door een derde lijn zijn de F-hoeken en de Z-hoeken gelijk.

In de figuur zie je wat F-hoeken en Z-hoeken zijn.

Omdat het opbouwen van de gehele theorie der vlakke meetkunde teveel tijd kost, is er voor het leveren van bewijzen een lijst van definities en stellingen ontwikkeld die als uitgangspunt mogen worden genomen en die je dus moet kennen. De schuin gedrukte en onderstreepte termen dienen als verwijzing in een bewijs. Je vindt deze lijst via

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Basisbegrippen > Theorie

‡

Voorbeeld 1

Uitspraak: "Als de lijnen m en n evenwijdig zijn met de lijn l, dan zijn m en n ook evenwijdig aan elkaar."

Dit lijkt een simpele uitspraak. Maar omdat hij niet bij de axioma's hoort, moet je hem daaruit kunnen afleiden. Laat zien hoe.

Antwoord

Uit axioma 2 volgt dat als dit niet waar is, m en n elkaar snijden in een punt S.
En dan zouden er twee lijnen door S gaan die elk evenwijdig zijn met l.
En dat is volgens axioma 3 onmogelijk.
De uitspraak is daarom algemeen waar, het is een stelling.

Dit is een voorbeeld van een bewijs uit het ongerijmde: je toont aan dat uit het niet waar zijn van de uitspraak een tegenspraak met de axioma's volgt. De uitspraak moet dan wel waar zijn.

‡

Voorbeeld 2

Uitspraak: "Als elk van de benen van een hoek loodrecht staat op een van de benen van een andere hoek, dan zijn die hoeken gelijk."

Dit lijkt een goede uitspraak. Maar als je wat met de applet op

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Meetkunde > Redeneren en bewijzen > Basisbegrippen > Theorie

speelt (rode punten verplaatsen), vind je vast wel een voorbeeld waarin die uitspraak onwaar is, een tegenvoorbeeld. De uitspraak (een vermoeden) kan daarom geen stelling worden, hij is niet algemeen geldig.

‡

Voorbeeld 3

Het doel van dit wiskundedomein is het leren leveren van bewijzen voor stellingen. Wiskundigen doen dit uitgaande van al eerder bewezen stellingen en heldere definities van (nieuwe) begrippen (binnen een bepaalde theorie). Voor de vlakke meetkunde zijn de axioma's (plus definities e.d.) van Euclides het vaststaande uitgangspunt. Maar je kent al veel stellingen die daaruit voortvloeien (en die eigenlijk een strak bewijs behoeven!) die je niet steeds weer opnieuw wilt bewijzen. Daarom bestaat er een lijst van definities en stellingen die als uitgangspunt mogen worden genomen. Van daar uit probeer je zelf nieuwe stellingen te bewijzen.
Om de structuur van bewijzen duidelijk te maken zie je hier in voorbeelden enkele bewijzen van stellingen die op die lijst voorkomen.

Stelling:

De overstaande hoeken bij twee snijdende lijnen zijn gelijk.

Bewijs

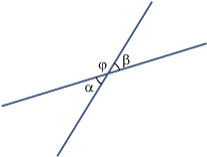
Laat α en β twee overstaande hoeken zijn.
Beide hebben dezelfde nevenhoek φ.
Dus is α + φ = 180° en is ook β + φ = 180°. Hieruit volgt: α = β.

Stelling:

De som van de hoeken van een driehoek is 180°.

Bewijs

Trek door (bijvoorbeeld) C een lijn evenwijdig aan lijnstuk AB. (Dit kan volgens axioma 3)
Je ziet nu bij punt C twee nieuwe hoeken ontstaan waarvan er één gelijk is aan ∠A en één gelijk is aan ∠B. (Volgens axioma 5)
Samen met ∠C vormen deze hoeken een gestrekte hoek. (Volgens definitie gestrekte hoek)

‡

Voorbeeld 4

Bij een bewijs uit het ongerijmde ga je er van uit dat wat je wilt bewijzen niet waar is. Daaruit leid je een tegenspraak af met het gegeven of met een al bekende stelling.

Bewijs hiermee: "Als twee lijnen gesneden worden door een derde lijn en de F-hoeken zijn gelijk, dan zijn die twee lijnen evenwijdig."

Bewijs

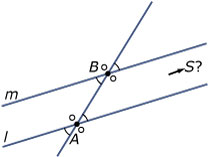Bij twee gelijke F-hoeken zijn ook hun overstaande hoeken gelijk.
En de vier nevenhoeken van al die F-hoeken zijn ook gelijk.
De acht hoeken in de figuur zijn dus vier aan vier gelijk.

Neem nu aan dat beide lijnen l en m niet evenwijdig zijn, dus elkaar snijden in S. Kijk naar twee hoeken tussen de twee lijnen en de derde lijn aan de kant waar S ligt. Die twee hoeken zijn hoeken van driehoek ASB.
Één van hen is gelijk aan de nevenhoek van de F-hoek van de andere.
Omdat de F-hoeken gelijk zijn, zijn de twee hoeken samen 180°.
Maar dat is onmogelijk omdat het maar twee hoeken van een driehoek zijn en de som van de hoeken van een driehoek 180° is. De aanname dat beide lijnen elkaar snijden is dus onjuist, ze zijn evenwijdig.

‡

Opgaven

5. In Voorbeeld 1 wordt een eenvoudige uitspraak bewezen.
   1. Wat is het verschil tussen een vermoeden en een stelling?
   2. Waarom is ook voor zo'n eenvoudige uitspraak een bewijs nodig?
   3. Wat is een tegenvoorbeeld?
   4. Waarom heet een bewijs uit het ongrijmde zo?


6. In Voorbeeld 2 wordt een vermoeden beschreven.
   1. Schrijf nog eens nauwkeurig op wat het vermoeden is dat daar wordt geuit. Maak zelf een tekening bij het opschrijven van het vermoeden, zet letters bij hoekpunten en snijpunten. Gebruik die letters in de beschrijving van het vermoeden.
   2. Teken een situatie waarin het vermoeden niet juist is en beschrijf wat er fout gaat.
   3. Waarom is slechts één tegenvoorbeeld genoeg om te bewijzen dat het vermoeden niet waar is?
   4. Kun je het vermoeden iets anders formuleren zodat het wel kan worden bewezen? Welke stelling krijg je?


7. Bekijk in Voorbeeld 3 het bewijs dat de hoeken van een driehoek samen 180° zijn.
   1. Welke van de vijf axioma's van Euclides speelt in dit bewijs een grote rol?
   2. Teken zelf de figuur bij dit bewijs en verleng zijde `AC` aan de kant van `C`.
   Bij punt `C` tref je nu drie hoeken aan. Eén daarvan zit in de driehoek `ABC` en heet daarom een binnenhoek van deze driehoek. De twee andere vormen samen een buitenhoek van `Delta ABC`. `/_A` en `/_B` zijn ook binnenhoeken van de driehoek. Het zijn de niet-aanliggende binnenhoeken van de buitenhoek van `/_C`.
   3. Bewijs nu zelf de stelling: In een driehoek is elke buitenhoek gelijk aan de som van de niet-aanliggende binnenhoeken.


8. De lijnen `l` en `m` staan loodrecht op elkaar, `s` is een derde lijn.
   1. Bewijs de stelling: Als `s` loodrecht staat op `l`, is `s` evenwijdig met `m`.
   2. Schrijf het omgekeerde van deze stelling op. Is dit ook een ware bewering?


9. Bekijk in Voorbeeld 4 nog eens een bewijs uit het ongerijmde. Bekijk nu de stelling: In `Delta ABC` is `/_A` stomp. Het voetpunt van de loodlijn uit `C` op `AB` ligt op het verlengde van `BA`.
   1. Laat zien dat punt `D` niet kan samenvallen met punt `A`. Beschrijf de tegenspraak waar dit toe leidt.
   2. Laat zien dat punt `D` niet tussen `A` en `B` kan liggen of met `B` kan samenvallen of op het verlengde van `AB` kan liggen.
   3. Waarom is hiermee de stelling bewezen?

Verwerken

10. Als een driehoek rechthoekig is, dan is één van de zijden langer dan de andere twee zijden.
    1. Is dat waar?
    2. Is het omgekeerde van deze uitspraak waar?
    3. Wat kun je over de hoeken van een driehoek zeggen als één van de zijden langer is dan de andere?


11. Strikt genomen is evenwijdigheid wel gedefinieerd voor lijnen maar niet voor lijnstukken.
    1. Bij een gegeven lijnstuk is er precies één lijn waar dat lijnstuk op ligt. Waarom?
    2. Bedenk een definitie voor evenwijdigheid van lijnstukken.


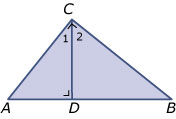12. Driehoek `ABC` heeft een rechte hoek bij `C`. Vanuit `C` is een loodlijn getrokken op `AB`.
    Bewijs dat `/_A = /_C_2` en dat `/_B = /_C_1`.
    


13. In deze opdracht geef je een ander bewijs voor de stelling dat in een driehoek de som van de hoeken 180° is. Je bewijst de stelling eerst voor rechthoekige driehoeken en daarna voor een willekeurige driehoek.
    1. Teken een rechthoek `ABCD` en teken daarin de diagonaal `AC`. Waarom is `/_CAB = /_ACD`?
    2. Bewijs dat in een rechthoekige driehoek de som van de hoeken 180° is.
    3. Teken nu een willekeurige scherphoekige driehoek `ABC` en teken de loodlijn vanuit `C` op `AB`. In de driehoek heb je twee rechthoekige driehoeken gekregen. Bewijs hiermee, en met het voorgaande, dat de som van de hoeken 180° is.
    4. Je hebt de stelling bewezen voor scherphoekige driehoeken. Geef een bewijs voor stomphoekige driehoeken.

Testen

14. Gegeven een stomphoekige driehoek. Bewijs uit het ongerijmde dat de driehoek twee scherpe hoeken heeft.
    


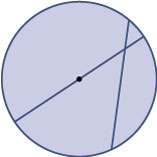15. Bekijk een koorde van een cirkel (dat is het lijnstuk tussen twee punten op de cirkel).
    1. Wat vermoed je over de lengte van die koorde, vergeleken met de lengte van een middellijn?
    2. Als je vermoeden klopt, moet je het kunnen bewijzen. Probeer dat met hulplijnen.
    3. Er doet zich een speciaal geval voor. Heb je daar rekening mee gehouden?