- Gaat op dezelfde manier, neem `/_B` stomphoekig.
- Z-hoeken zijn hoeken die een lijn `l` maakt met twee evenwijdige lijnen `m` en `n` en tussen de twee evenwijdige lijnen zitten aan weerskanten van `l`, de éne hoek bij het snijpunt met `m`, de andere bij het snijpunt met `n`. Alleen als de lijnen evenwijdig zijn, zijn de Z-hoeken gelijk.
- Neem op de aardbol punt `N` (de noordpool) en de punten `A` en `B` op de evenaar. De "lijnen" `NA` en `NB` over het aardoppervlak staan loodrecht op de evenaar. Dus is `/_A = /_B = 90`°. Dan moet `/_A + /_B + /_C > 180`° zijn.
- Noem het lijnstuk `AB`. Teken een halve lijn `l` uit `A`. Pas op lijn `l` vanuit `A` vier gelijke stukken af, je krijgt dan achtereenvolgens `AP`, `PQ`, `QR` en `RS`. Verbindt het eindpunt `S` met `B`. Construeer door de punten `P`, `Q` en `R` lijnen evenwijdig aan `SB`. De evenwijdige lijnen snijden `AB`. De snijpunten verdelen van het lijnstuk `AB` in vier gelijke delen.
- Construeer een vierkant en teken een van de diagonalen.
- Construeer een gelijkzijdige driehoek en teken de loodlijn uit een van de punten op de overstaande zijde.
- Zolang er geen bewijs voor een uitspraak is geleverd heet die uitspraak een vermoeden. Een stelling is een vermoeden waarvan het bewijs is geleverd.
- Omdat hij geen axioma is (geen uitgangspunt bij de theorieopbouw). En in elke goede theorie moet elk nieuw vermoeden worden bewezen, dus kunnen worden afgeleid uit de axioma's.
- Een voorbeeld waarmee je aantoont dat een bepaald uitspraak onwaar is.
- Zo'n bewijs heet zo omdat het aantoont dat het onwaar zijn van de stelling niet te rijmen is met de theorie, dus leidt tot een tegenspraak in de theorie.
- Als elk van de benen van een hoek loodrecht staan op de benen van een andere hoek, zijn de hoeken gelijk.
- Bekijk de applet in Voorbeeld 2. Het gaat fout als hoekpunt `B` tussen de benen van `/_A` komt te liggen. Dan zijn beide hoeken samen 180°.
- Als een uitspraak in één geval niet klopt is hij onwaar.
-
Als elk van de benen van een hoek loodrecht staan op de benen van een andere hoek, zijn de hoeken gelijk of ze zijn samen 180°.
Het bewijs van deze stelling kun je leveren als je wat meer weet over gelijkvormigheid van driehoeken, daarover gaan de volgende onderdelen...
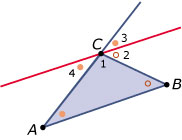
- Axioma 5 over gelijke F-hoeken en Z-hoeken bij evenwijdige lijnen.
- Zie figuur.
-
Je ziet dat `/_C_2 = /_B` (Z-hoeken) en `/_C_1 = /_A` (F-hoeken).
En dus is `/_C_(1,2) = /_A + /_B`. Waarmee de stelling bewezen is.
- Als de punten `A` en `D` samenvallen is `/_A` recht en dat is in tegenspraak met het gegeven dat hij stomp is.
- Als punt `D` tussen `A` en `B` ligt of met `B` samen valt of op het verlengde van `AB` ligt heeft `Delta CDA` zowel een stompe als een rechte hoek en dat is in tegenspraak met de stelling dat de som van de hoeken in een driehoek 180° is.
- Punt `D` ligt op het verlengde van `BA` is de enige mogelijkheid die overblijft en die moet dus waar zijn.
- De hoek tussen `s` en `l` is 90° en de hoek tussen `m` en `l` ook. Dit zijn twee F-hoeken. Dus de lijnen `s` en `m` zijn evenwijdig.
- Als lijn `s` evenwijdig is met `m`, staat lijn `s` ook loodrecht op `l`. De omgekeerde stelling is ook juist.
- De uitspraak is waar. Hij volgt onmiddellijk uit de bekende stelling van Pythagoras. (Eigenlijk moet je die stelling nog vanuit de axioma's afleiden, het bewijs dat je in opgave 2 tegenkwam vergt meer voorkennis dan je in feite nu vanuit de axioma's hebt afgeleid. Wel hoort de stelling van Pythagoras bij de lijst van stellingen en basisbegrippen waar je in een bewijs op het vwo-examen van uit mag gaan.)
- Nee, die uitspraak is niet waar.
- Tegenover de langste zijde van een driehoek ligt de grootste hoek.
- Door twee punten gaat maar één lijn.
- Twee lijnstukken zijn evenwijdig als de lijnen waarop de lijnstukken liggen evenwijdig zijn.
Op dezelfde manier bewijs je de andere stelling.
- Het zijn Z-hoeken.
- Omdat `/_BAC = /_ACD` is `/_BAC + /_ACB = 90`°. Omdat ook `/_B = 90`° is de som van de hoeken van de rechthoekige `Delta ABC` 180°.
-
In `Delta ADC` is `/_A + /_D_1 + /_C_1 = 180`°.
In `Delta BDC` is `/_B + /_D_2 + /_C_2 = 180`°.
Dus is `/_A + /_D_1 + /_C_1 + /_B + /_D_2 + /_C_2 = 360`°. En omdat `/_D_1 + /_D_2 = 180`° is ook `/_A + /_C_1 + /_B + /_C_2 = /_A + /_B + /_C = 180`°. -
Neem hoogtelijn `CD` met `D` op het verlengde van `BA` en bekijk de rechthoekige driehoeken `ACD` en `BCD`.
In `Delta ACD` is `/_A_1 + /_D + /_C_1 = 180`°.
In `Delta BDC` is `/_B + /_D + /_C_1 + /_C_2 = 180`°.
Dus is `/_A_1 + /_D + /_C_1 + /_B + /_D + /_C_1 + /_C_2 = 360`°. Nu is `/_A_1 = 180^(text(o)) - /_A_2` en `/_C_1 = 90^(text(o)) - /_A_1 = /_A_2 - 90^(text(o))`. Dit geeft: `/_B + /_A_2 + /_C_2 = 180`°.
Te bewijzen: `/_B` en `/_C` zijn scherp.
Bewijs: Neem aan dat `/_B` niet scherp is, dan is de som `/_A + /_B + /_C` meer dan 180°. Neem aan dat `/_C` niet scherp is, dan is de som `/_A + /_B + /_C` meer dan 180°. Dit leidt in beide gevallen tot een tegenspraak, dus `/_B` en `/_C` zijn beide scherp.
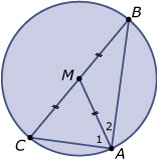
- Een koorde (waar het middelpunt niet op ligt) is korter dan de middellijn van de cirkel.
-
Gegeven: `AB` is koorde en `BC` is middellijn.
Te bewijzen: `AB < BC`.
Bewijs: `MA = MB = MC` geeft `/_C = /_A_1` en `/_B = /_A_2`. Omdat `/_A_1 + /_A_2 + /_B + /_C = 180`°, is `/_A_1 + /_A_2 = 90`°. Dit betekent dat `Delta ABC` rechthoekig is en van een rechthoekige driehoek zijn de rechthoekszijden korter dan de schuine zijde. - Het speciale geval is de situatie dat `M` op de koorde ligt. In dat geval zijn koorde en middellijn even lang.
