
Totaalbeeld
Samenvatten
Je hebt nu alle theorie van "Goniometrische functies" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!
Begrippenlijst:
61: goniometrische functie — de functie y = tan(x)
62: goniometrische formules: symmetrieformules, verdubbelingsformules, somformules, formules van Simpson — verbanden tussen sin en cos
63: afgeleiden van sin, cos en tan
64: harmonische trilling — frequentie en trillingstijd
65: primitieve van een goniometrische functie
Activiteitenlijst:
61: werken met goniometrische functies (o.a. y = tan(x)) op de GR
62: de goniometrische formules afleiden — de goniometrische formules gebruiken bij het herschrijven van goniometrische functies en het oplossen van vergelijkingen
63: de afgeleide van een goniometrische functie bepalen en toepassen
64: bepalen of een som van harmonische trillingen weer een harmonische trilling is
65: de primitieve van een goniometrische functie bepalen en toepassen
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Achtergronden
Testen
-
Gegeven zijn de functies `f(x) = sin(x + 1/3 pi) + 1` en `g(x) = 1 + sin(x)`.
Beide hebben ze als domein `[0, 2pi]`.
Verder is gegeven de functie `h` met `h(x) = f(x) - g(x)`.
-
Toon aan dat de grafiek van `h` een zuivere sinusoïde is. Bereken de amplitude en de evenwichtsstand van `h`.
-
Bereken algebraïsch de snijpunten van de grafieken van `f` en `g`.
-
Los op: `f(x) < g(x)`.
-
Los de volgende vergelijkingen algebraïsch op:
-
`sin(x) - cos(x - 1/4 pi) = 0`
-
`sin(x) - cos(x - 1/4 pi) = 1`
-
`sin^2(x) = 1 - 2 cos(2x)`
-
`tan(x) = cos(x)`
-
Gegeven is de functie `f(x) = sin(2x) + sin(x - 1/3 pi)` met domein `[-2pi, 2pi]`.
- Laat zien dat de grafiek van `f` geen zuivere sinusoïde is.
- Los algebraïsch op: `f(x) <= 0`.
- Bereken de hoek waaronder de grafiek van `f` de `y`-as snijdt.
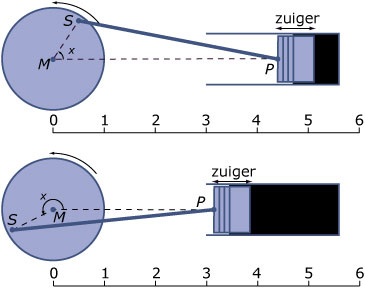 Een zuiger is door middel van een drijfstang verbonden met een draaiende schijf.
Als de schijf draait, beweegt de zuiger horizontaal heen en weer. `M` is het middelpunt
van de schijf. `S` is de (scharnierende) verbinding van de drijfstang met de
schijf. Bij punt `P` is de drijfstang scharnierend met de zuiger verbonden.
`MS = 1` en `PS = 4`.
Stel de grootte van de hoek `PMS` is `x` radialen. Dan is de afstand `PM` afhankelijk
van de hoekgrootte `x`. Er geldt: `PM = a(x)`. Voor elke hoekgrootte `x` geldt:
Een zuiger is door middel van een drijfstang verbonden met een draaiende schijf.
Als de schijf draait, beweegt de zuiger horizontaal heen en weer. `M` is het middelpunt
van de schijf. `S` is de (scharnierende) verbinding van de drijfstang met de
schijf. Bij punt `P` is de drijfstang scharnierend met de zuiger verbonden.
`MS = 1` en `PS = 4`.
Stel de grootte van de hoek `PMS` is `x` radialen. Dan is de afstand `PM` afhankelijk
van de hoekgrootte `x`. Er geldt: `PM = a(x)`. Voor elke hoekgrootte `x` geldt:
`a(x) = cos(x) + sqrt(16 - x^2)`
- Bewijs deze formule voor `0 < x < 1/2pi`.
In de grafiek van `a` op het domein `[0,2pi]` zie je dat het minimum van `a(x)` gelijk is aan `3` en het maximum gelijk is aan `5`.
- Hoe kun je dat berekenen aan de hand van de tekening van de zuiger?
-
Bij één rondgang van de schijf zal de lengte `PM` op twee momenten gelijk zijn aan de lengte van de drijfstang `PS`.
Hoe groot zijn de hoeken `PMS` waarbij zich dat voordoet? Geef je antwoord in radialen en in één decimaal nauwkeurig.
-
De afstand `a(x)` kun je benaderen door de formule `b(x) = 4 + cos(x)`.
Onderzoek voor welke `x` het verschil tussen `b(x)` en `a(x)` maximaal is en bereken dit in twee decimalen nauwkeurig.
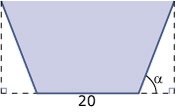 Het Ministerie van Ontwikkelingssamenwerking geeft een bedrijf opdracht om goten te ontwikkelen voor een bevloeiingssysteem in een ontwikkelingsland. Deze goten krijgen de vorm van langwerpige bakken met twee opstaande randen die een hoek van `alpha` (in radialen) maken met de horizontale bodem. De dwarsdoorsnede van de goot is een gelijkbenig trapezium, de breedte van de bodem is net als die van de opstaande randen `20` cm.
Het Ministerie van Ontwikkelingssamenwerking geeft een bedrijf opdracht om goten te ontwikkelen voor een bevloeiingssysteem in een ontwikkelingsland. Deze goten krijgen de vorm van langwerpige bakken met twee opstaande randen die een hoek van `alpha` (in radialen) maken met de horizontale bodem. De dwarsdoorsnede van de goot is een gelijkbenig trapezium, de breedte van de bodem is net als die van de opstaande randen `20` cm.
- Hoeveel liter water kan de goot per meter verwerken als `alpha = 0,25`?
- Toon aan dat de hoeveelheid water (in L) die de goot per meter kan verwerken gelijk is aan: `W(alpha) = 40 sin(alpha) + 40 sin(alpha)* cos(alpha)`.
- Bereken de waarde van `alpha` waarvoor `W` zo groot mogelijk is in één decimaal nauwkeurig.
- Is dit zonder meer de meest gunstige manier van buigen? Verklaar je antwoord.
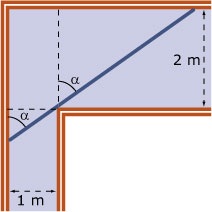 Door een smalle gang moet een houten paneel van 400 cm bij 90 cm worden vervoerd. De dikte van het paneel is te verwaarlozen. Je ziet in de figuur
een bovenaanzicht van de hoek die er in de gang zit. Het paneel wordt tijdens het vervoer verticaal gehouden. De gang is `2,80` m hoog. De vraag is nu of het paneel de bocht kan maken.
Stel je voor dat `l` de grootste lengte is die nog de bocht om kan.
Door een smalle gang moet een houten paneel van 400 cm bij 90 cm worden vervoerd. De dikte van het paneel is te verwaarlozen. Je ziet in de figuur
een bovenaanzicht van de hoek die er in de gang zit. Het paneel wordt tijdens het vervoer verticaal gehouden. De gang is `2,80` m hoog. De vraag is nu of het paneel de bocht kan maken.
Stel je voor dat `l` de grootste lengte is die nog de bocht om kan.
-
Laat zien dat uit deze tekening volgt: `l = 1/(sin(alpha)) + 2/(cos(alpha))`.
Hierin is `alpha` in radialen met `0 <= alpha <= 1/2pi`.
-
Laat zien dat `l` een maximale waarde heeft.
-
Kan een paneel met een lengte van `4` m deze bocht halen?
Toepassen
Constructies met passer en liniaal
Als je twee harmonische trillingen combineert die slechts weinig in frequentie
verschillen, dan ontstaat een verschijnsel dat zweving heet. Voor geluid betekent
dit dat het afwisselend sterker en zwakker wordt. Zie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Toepassingen
Stel in de applet naast de trilling `u_1(t) = sin(2pi * 440 * t)` de trilling `u_2(t) = sin(2pi * 430 * t)` met `t` in seconden.
-
Je hoort deze trillingen tegelijk. Bekijk de grafiek van de resulterende trilling. Waaraan herken je de zweving?
-
De amplitude van de trilling is een maat voor de sterkte van het geluid. Tussen welke waarden zweeft de resulterende trilling?
Welk verband is er met de amplitudes van de twee afzonderlijke harmonische trillingen?
-
Onderzoek of zweving zich altijd voordoet als de frequenties van twee trillingen verschillen.
Als dat niet het geval is, probeer dan vast te leggen wanneer zweving zich wel voordoet.
Is er verband tussen de waarden waartussen de geluidssterkte zweeft en de amplitudes van de afzonderlijke harmonische trillingen?
Gedempte trillingen
Een gedempte trilling is een trilling waarvan de amplitude met de tijd afneemt. In praktische situaties heb je bijna altijd met demping te maken: wegstervend geluid, een steeds minder uitslaande slinger, een veer die steeds minder trilt...
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Toepassingen
Je ziet daar een gedempte trilling `u(t)` waarvan de amplitude exponentieel afneemt: `A = g^t`.
- Waarom is exponentiële afname in praktijksituaties van de amplitude voor de hand liggender dan lineaire afname?
Beschrijf een paar van die praktijksituaties.
- Neem `g = 0,8`. Na hoeveel tijd is de amplitude dan telkens gehalveerd?
- Bij een periode van `p = 1` heeft `u(t)` een maximum op `t = 0,25`. Hoe groot is dit maximum? Is er een maximum dat precies de helft van dit maximum is?
Zo ja, op welk tijdstip?
Examenopgaven
Twee scharnierende vierkanten
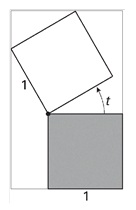
Twee vierkanten, beide met zijde `1`, hebben het hoekpunt `O` gemeenschappelijk. Het
onderste vierkant ligt vast. Het bovenste vierkant wordt om `O` gedraaid; `t` is de draaihoek in
radialen. In de volgende figuur zijn tussen de begin- en eindstand drie tussenstanden getekend. Om de
twee vierkanten is steeds een zo klein mogelijke rechthoek getekend, met twee zijden langs het vaste vierkant.

 De oppervlakte `R` van de omhullende rechthoek is een functie van de draaihoek `t`.
De oppervlakte `R` van de omhullende rechthoek is een functie van de draaihoek `t`.
Voor elke waarde van `t` tussen `0` en `1/2 pi` geldt: `R(t) = (1 + sin(t))(1 + sin(t) + cos(t))`.
In de figuur hiernaast is de situatie getekend voor een waarde van `t` tussen `0` en `1/2 pi`.
-
Toon de juistheid van de formule aan voor elke waarde van `t` tussen `0` en `1/2 pi`.
-
Teken de posities van de vierkantjes waarvoor `R(t)` maximaal is. Licht je werkwijze toe.
-
Toon met behulp van differentiëren aan dat `R'(0) = 3`.
(bron: examen wiskunde B vwo 2003, eerste tijdvak)
Een verzameling functies
Op het domein `[0, 2pi]` zijn gegeven de functies: `f_(n) (x) = 1 + sin^2(x) + cos(nx)` waarbij `n` een positief geheel getal is.
De grafiek van `f_n` gaat voor bepaalde waarden van `n` door het punt `(1/6 pi, 1/4)`.
- Onderzoek voor welke waarden van `n` tussen `0` en `50` dit geldt.
- `f_(4)(x)` is te schrijven als `f_(4) (x) = 1,5 - 0,5cos(2x) + cos(4x)`. Toon aan dat dit juist is.
Gegeven is de rechthoek `OABC` met `A(2pi, 0)` en `C(0, 3)`. De grafiek van `f_4` verdeelt deze rechthoek in twee gebieden.
- Toon aan met behulp van integreren dat deze twee gebieden exact dezelfde oppervlakte hebben.
(bron: examen wiskunde B vwo 2004, eerste tijdvak)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Achtergronden Een zuiger is door middel van een drijfstang verbonden met een draaiende schijf.
Als de schijf draait, beweegt de zuiger horizontaal heen en weer. `M` is het middelpunt
van de schijf. `S` is de (scharnierende) verbinding van de drijfstang met de
schijf. Bij punt `P` is de drijfstang scharnierend met de zuiger verbonden.
`MS = 1` en `PS = 4`.
Stel de grootte van de hoek `PMS` is `x` radialen. Dan is de afstand `PM` afhankelijk
van de hoekgrootte `x`. Er geldt: `PM = a(x)`. Voor elke hoekgrootte `x` geldt:
Een zuiger is door middel van een drijfstang verbonden met een draaiende schijf.
Als de schijf draait, beweegt de zuiger horizontaal heen en weer. `M` is het middelpunt
van de schijf. `S` is de (scharnierende) verbinding van de drijfstang met de
schijf. Bij punt `P` is de drijfstang scharnierend met de zuiger verbonden.
`MS = 1` en `PS = 4`.
Stel de grootte van de hoek `PMS` is `x` radialen. Dan is de afstand `PM` afhankelijk
van de hoekgrootte `x`. Er geldt: `PM = a(x)`. Voor elke hoekgrootte `x` geldt:
 Het Ministerie van Ontwikkelingssamenwerking geeft een bedrijf opdracht om goten te ontwikkelen voor een bevloeiingssysteem in een ontwikkelingsland. Deze goten krijgen de vorm van langwerpige bakken met twee opstaande randen die een hoek van `alpha` (in radialen) maken met de horizontale bodem. De dwarsdoorsnede van de goot is een gelijkbenig trapezium, de breedte van de bodem is net als die van de opstaande randen `20` cm.
Het Ministerie van Ontwikkelingssamenwerking geeft een bedrijf opdracht om goten te ontwikkelen voor een bevloeiingssysteem in een ontwikkelingsland. Deze goten krijgen de vorm van langwerpige bakken met twee opstaande randen die een hoek van `alpha` (in radialen) maken met de horizontale bodem. De dwarsdoorsnede van de goot is een gelijkbenig trapezium, de breedte van de bodem is net als die van de opstaande randen `20` cm.
 Door een smalle gang moet een houten paneel van 400 cm bij 90 cm worden vervoerd. De dikte van het paneel is te verwaarlozen. Je ziet in de figuur
een bovenaanzicht van de hoek die er in de gang zit. Het paneel wordt tijdens het vervoer verticaal gehouden. De gang is `2,80` m hoog. De vraag is nu of het paneel de bocht kan maken.
Stel je voor dat `l` de grootste lengte is die nog de bocht om kan.
Door een smalle gang moet een houten paneel van 400 cm bij 90 cm worden vervoerd. De dikte van het paneel is te verwaarlozen. Je ziet in de figuur
een bovenaanzicht van de hoek die er in de gang zit. Het paneel wordt tijdens het vervoer verticaal gehouden. De gang is `2,80` m hoog. De vraag is nu of het paneel de bocht kan maken.
Stel je voor dat `l` de grootste lengte is die nog de bocht om kan.
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Toepassingen![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Totaalbeeld > Toepassingen
 De oppervlakte `R` van de omhullende rechthoek is een functie van de draaihoek `t`.
De oppervlakte `R` van de omhullende rechthoek is een functie van de draaihoek `t`.