Harmonische trilling

Inleiding

Als iemand muziek maakt hoor je tonen. Die tonen ontstaan meestal door trilling van een snaar, of van lucht in een of andere holte. Trillingen kun je goed zien door te kijken naar een trillende snaar. De hoogte van de toon hangt af van de lengte van de snaar: hoe vaker hij per seconde trilt, hoe hoger de toon. De centrale A van de piano trilt met 440 Hz (hertz = trillingen per seconde). Het is een voorbeeld van een harmonische trilling.

Je leert nu:

• harmonische trillingen beschrijven m.b.v. sinusoïden;
• sinusoïden optellen en onderzoeken of er dan opnieuw sprake is van een sinusoïde;
• de somformules en de formule voor a sin(x) + b cos(x) toepassen.

Je kunt al:

• de somformules voor goniometrische functies gebruiken;
• werken met sinusoïden;
• goniometrische functies differentiëren.

Verkennen

Als iemand muziek maakt hoor je tonen. Die tonen ontstaan meestal door trilling van een snaar, of van lucht in een of andere holte. Trillingen kun je goed zien door te kijken naar een trillende snaar. De hoogte van de toon hangt af van de lengte van de snaar: hoe vaker hij per seconde trilt, hoe hoger de toon. De "kamertoon", de centrale A van de piano trilt met 440 Hz (hertz = trillingen per seconde). Het is een voorbeeld van een harmonische trilling.

Bij deze A hoort een harmonische trilling volgens u(t) = sin(440 · 2πt) waarin u de uitwijking van de trilling en t de tijd in seconden is.

> Breng de bijbehorende grafiek in beeld op de GR, precies twee periodes.

Behalve deze grondtoon klinken er ook boventonen mee, de eerste boventoon heeft de dubbele frequentie en de tweede heeft een frequentie die drie keer zo groot is, etc. Elke boventoon klinkt vaak minder sterk dan de grondtoon. Met behulp van de Geluidsapplet kun je een toon van een instrument laten horen en het trillingspatroon bekijken. Je kunt dan met de schuifregelaars dit patroon zelf maken.

> Bekijk het trillingspatroon van een A van 440 Hz gespeeld op de klarinet. Maak zelf dit trillingspatroon na met de applet.
> Welke formule hoort er bij?
> Doe dit ook met de andere instrumenten.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Goniometrische functies > Harmonische trilling > Uitleg

Een harmonische trilling is een periodieke beweging die wordt beschreven door een sinusoïde. Een goed voorbeeld is een veer met een gewichtje er aan wat in trilling wordt gebracht. De uitwijking uit de evenwichtststand heeft dan bijvoorbeeld een formule van de vorm u(t) = 4 sin(4πt), waarin u de uitwijking uit de evenwichtsstand in cm is en t de tijd in seconden.
De periode van deze trilling is $\frac{2\pi }{4\pi }$ = 0,5 seconde.

In de applet kun je twee harmonische trillingen instellen. Soms zijn ze "in fase" (ze starten dan op hetzelfde moment), soms niet. Ze hebben dezelfde amplitude, de evenwichtstand is 0 (er zijn drie tijdassen). Als je ze optelt (ze werken dan tegelijkertijd) kunnen ze elkaar versterken, dan wel uitdoven.
Altijd ontstaat er een nieuwe periodieke functie, niet altijd is het weer een harmonische trilling, een sinusoïde. Wanneer wel en wanneer niet?

Even experimenteren en je zult wel vermoeden dat dit te maken heeft met de periodes van u₁ en u₂: alleen als die gelijk zijn krijg je weer een zuivere sinusoïde.

‡

Opgaven

1. Bekijk de applet in de Uitleg. Gebruik de begininstellingen `p=1`, `q=1` en `r=0` en bekijk de grafieken van `u_1`, `u_2` en `u_3 = u_1 + u_2`.
   1. Laat algebraïsch zien dat `u_3` een sinusoïde is.
   2. Hebben `u_1` en `u_2` een faseverschil?
   Je gaat nu `r` variëren.
   3. Neem bijvoorbeeld `r = 0,25` en probeer nog wat andere waarden voor `r`. Wat gebeurt er met `u_3`? Laat dit ook algebraïsch zien.
   4. Bij welke waarden van `r` wordt `u_3` een rechte lijn?


2. Bekijk weer de applet in de Uitleg. Gebruik de begininstellingen `p=1`, `q=0,5` en `r=0` en bekijk de grafieken van `u_1`, `u_2` en `u_3 = u_1 + u_2`.
   1. De periodes van `u_1` en `u_2` zijn nu verschillend. Is `u_3` een sinusoïde?
   2. Experimenteer met de applet. Wanneer wordt `u_3` een sinusoïde?
   3. Je kunt de formule van `u_3` herleiden met de formules van Simpson. Hoe kun je daarna zien dat er alleen een sinusoïde kan ontstaan als de periodes van `u_1` en `u_2` gelijk zijn?


3. In deze applet kun je de amplitudes van `u_1` en `u_2` niet veranderen. Daarom kun je de formules van Simpson toepassen. Maar bekijk nu de functies `u_1 = sin(2pi t)` en `u_2 = 2 sin(2pi (t - 1))`.
   1. Breng `u_3 = u_1 + u_2` in beeld op de grafische rekenmachine (of in GeoGebra).
   2. Lijkt `u_3` een sinusoïde te zijn?
   3. Kun je dit ook algebraïsch aantonen?

Theorie

Een harmonische trilling is een periodieke beweging die wordt beschreven door een sinusoïde. Een goed voorbeeld is een veer met een gewichtje er aan wat in trilling wordt gebracht. De uitwijking u (in m) uit de evenwichtststand is een functie van de tijd t (in s):
u(t) = A $\sin \left(\frac{2\text{π}}{p}\cdot t\right)$ met:

• amplitude (maximale uitwijking) A
• periode of trillingstijd (de tijdsduur van één trilling) p
• frequentie (aantal trillingen per s) f = $\frac{1}{p}$

Tel je twee harmonische trillingen bij elkaar op, dan zijn er verschillende mogelijkheden:

• Beide sinusoïden hebben dezelfde amplitude en periode maar de éne is horizontaal verschoven t.o.v. de andere. Die horizontale verschuiving noem je het faseverschil.
  Is er alleen sprake van een faseverschil dan levert de optelling van beide sinusoïden opnieuw een sinusoïde op: de som van twee harmonische trillingen is dan weer een harmonische trilling. Zie Voorbeeld 1.
• Beide sinusoïden hebben alleen dezelfde periode. Er is zowel een faseverschil als een verschil in amplitude. Ook in dit geval is de som van twee harmonische trillingen opnieuw een harmonische trilling. Zie Voorbeeld 2.
• Beide sinusoïden hebben verschillende periodes. Nu is de som van twee harmonische trillingen geen zuiver harmonische trilling. Zie Voorbeeld 3.

‡

Voorbeeld 1

Gegeven de twee harmonische trillingen u₁ en u₂ door:
u₁(t) = sin(t) en u₂(t) = sin(t – 2).
Beide trillingen hebben dezelfde periode en amplitude. Toon aan dat u = u₁ + u₂ ook een harmonische trilling is.

Antwoord

In dit geval (gelijke periodes en gelijke amplitudes) zijn de formules van Simpson goed bruikbaar:
u(t) = sin(t) + sin(t – 2) = 2 sin(t – 1) cos(1) ≈ 1,08 sin(t – 1)

Je krijgt dus door u₁ en u₂ op te tellen een sinusoïde met een amplitude van ongeveer 1,08 en een periode van 2π.
Iets dergelijks vind je steeds als je twee harmonische trillingen met gelijke periodes en gelijke amplitudes optelt: de som is dan weer een harmonische trilling. Als de éne formule een sinus en de andere een cosinusfunctie is, zet je die cos-functie eerst om in een sinus (of de sin in een cos).

‡

Voorbeeld 2

Gegeven de twee harmonische trillingen u₁ en u₂ door:
u₁(t) = 2 sin(t) + 1 en u₂(t) = sin(t – 2).
Beide trillingen hebben alleen dezelfde periode. Toon aan dat u = u₁ + u₂ ook een harmonische trilling is.

Antwoord

Omdat de amplitudes verschillen kun je de formules van Simpson niet toepassen. Wel kun je sin(t – 2) uitwerken:
sin(t – 2) = sin(t) cos(2) – cos(t) sin(2).

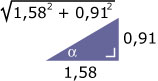
Hiermee wordt: u(t) ≈ 1,58 sin(t) – 0,91 cos(t) + 1.
Nu is er een hoek α met: cos(α) = $\frac{\mathrm{1,58}}{\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}}$  en  sin(α) = $\frac{\mathrm{0,91}}{\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}}$
En dus is:
u(t) ≈ $\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}$ · (sin(t) · $\frac{\mathrm{1,58}}{\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}}$ – cos(t) · $\frac{\mathrm{0,91}}{\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}}$) + 1 = 
       = $\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}$ · (sin(t) cos(α) – cos(t) sin(α)) + 1 =
       = $\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}$ · sin(t – α) + 1
De hoek α bereken je uit tan(α) = $\frac{\mathrm{0,91}}{\mathrm{1,58}}$.

u is een harmonische trilling met u(t) ≈ $\sqrt{{\mathrm{1,58}}^2+{\mathrm{0,91}}^2}$ · sin(t – 0,52) + 1.

‡

Voorbeeld 3

Gegeven de twee harmonische trillingen u₁ en u₂ door:
u₁(t) = sin(t) en u₂(t) = sin(2t).
Beide trillingen hebben verschillende periodes. Toon aan dat u = u₁ + u₂ geen harmonische trilling is.

Antwoord

Omdat u₁ en u₂ dezelfde amplitudes hebben, kun je de formules van Simpson toepassen.
Je vindt dan: u(t) = sin(t) + sin(2t) = 2 sin(1,5t) cos(0,5t).

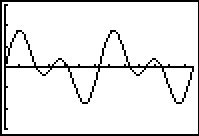Deze formule heeft niet de gedaante van een sinusoïde.
Maar u(t) is wel periodiek.
Omdat sin(t) zich herhaalt met een periode van 2π en sin(2t) met een periode van π, past de trillingstijd van de sin(2t) precies twee keer in die van sin(t). De periode is daarom 2π.
(In het algemeen is in een dergelijk geval de periode het kleinste gemeenschappelijke veelvoud van beide afzonderlijke periodes.)

‡

Opgaven

4. In Voorbeeld 1 zie je hoe twee harmonische trillingen `u_1` en `u_2` met dezelfde periode en amplitude worden opgeteld. Met de formules van Simpson kun je aantonen dat `u(t) = u_1(t) + u_2(t)` weer een sinusoïde is. Laat dit zelf zien als
   1. `u_1(t) = sin(t)` en `u_2(t) = sin(t - 2) + 4`
   2. `u_1(t) = sin((2pi)/5 t)` en `u_2(t) = sin((2pi)/5 (t - 2)) + 4`
   3. `u_1(t) = cos((2pi)/5 t)` en `u_2(t) = sin((2pi)/5 (t - 2)) + 4`
   4. `u_1(t) = cos((2pi)/5 t)` en `u_2(t) = cos((2pi)/5 (t + 3)) + 2`


5. In Voorbeeld 2 zie je hoe twee harmonische trillingen `u_1` en `u_2` met dezelfde periode worden opgeteld. Nu zijn echter de amplitudes verschillend. Bekijk goed hoe in dit voorbeeld wordt aangetoond dat er toch sprake is van een sinusoïde.
   1. Breng de grafiek van `u(t)` in beeld op je grafische rekenmachine. Ga na dat hij op een sinusoïde lijkt en bepaal frequentie, amplitude en evenwichtslijn.
   2. Werk nu zelf het voorbeeld na. Bekijk goed hoe de amplitude van de sinusoïde wordt gevonden.
   3. Laat op dezelfde manier zien, dat `v(t) = u_1(t) - u_2(t)` een sinusoïde is.


6. Gegeven is `u_1(t) = 3 sin(t)` en `u_2(t) = 4 cos(t)`.
   1. Toon aan dat `u_3(t) = u_1(t) + u_2(t)` een sinusoïde is. Bereken de amplitude en de horizontale verschuiving ten opzichte van `y = sin(x)`.
   2. Toon aan dat `u_4(t) = u_1(t) - u_2(t)` een sinusoïde is. Bereken de amplitude en de horizontale verschuiving ten opzichte van `y = sin(x)`.
   3. Toon aan dat `u_5(t) = -u_1(t) + u_2(t)` een sinusoïde is. Bereken de amplitude en de horizontale verschuiving ten opzichte van `y = sin(x)`.


7. Gegeven zijn de functies `f(x) = 4 sin(2x)` en `g(x) = 2 cos(2x - 5) + 1`. Het zijn beide sinusoïden. Verder is `S(x) = f(x) + g(x)`.
   1. Waarom is `S` weer een sinusoïde?
   2. Bewijs dat `S` een sinusoïde is en bereken de amplitude en de horizontale verschuiving ten opzichte van `y = sin(x)`.
   3. Los op: `S(x) = 2`.


8. Bekijk de twee harmonische trillingen in Voorbeeld 3. Hun som is geen harmonische trilling.
   1. Waarom niet?
   Neem nu `u_1(t) = sin(3t)` en `u_2(t) = sin(4t)`.
   2. De grafiek van `u(t) = u_1(t) + u_2(t)` is geen harmonische trilling, maar wel periodiek. Toon dit aan.
   3. Hoe leid je de periode van `u` af uit die van `u_1` en die van `u_2`?

Verwerken

9. Ga nog eens uit van twee harmonische trillingen `u_1` en `u_2`. Onderzoek in de elk van de volgende gevallen uit of `u(t) = u_1(t) + u_2(t)` weer een harmonische trilling is. Bepaal in dat geval de frequentie en amplitude.
   1. `u_1 = 2 cos(t)` en `u_2 = 5 + sin(t)`
   2. `u_1 = 2 cos(50pi t)` en `u_2 = 5 + sin(50pi t)`
   3. `u_1 = 2 cos(50pi t)` en `u_2 = 5 + sin(50pi (t - 2))`
   4. `u_1 = 2 cos(50pi t)` en `u_2 = 5 + sin(100pi t)`


10. Van een aangeslagen pianosnaar zijn de grondtoon en de eerste boventoon hoorbaar. Voor de grondtoon geldt de formule `u_0 = sin(880pi t)`. De eerste boventoon heeft de dubbele frequentie en een amplitude die half zo groot is.
    1. Het geluid dat deze snaar produceert ontstaat door beide trillingen op te tellen. Welke formule geldt voor de trilling van de snaar?
    2. Waarom trilt de snaar niet zuiver harmonisch? Welke frequentie heeft de trilling?
    De tweede boventoon heeft een drie maal zo hoge frequentie als de grondtoon. De amplitude is de helft van de eerste boventoon. Veronderstel dat ook die tweede boventoon hoorbaar is.
    3. Welke formule geldt er dan voor de uitwijking van de pianosnaar? Met welke frequentie trilt de snaar?


11. Je kunt met een hoorn lage tonen spelen. Zo’n toon heeft bijvoorbeeld een frequentie van `80` Hz. De toon kun je voorstellen door een sinuoïde met een amplitude van `10`.
    Op een hobo speel je hogere tonen met een frequentie van bijvoorbeeld `400` Hz. Deze toon kun je je voorstellen door een sinusoïde met een amplitude van `5`.
    1. Stel voor beide tonen een formule op voor de bijbehorende sinusoïde.
    2. Iemand hoort de beide tonen tegelijk. Teken de grafiek van de toon die hij hoort. Zorg ervoor dat er precies twee periodes zichtbaar zijn.
    3. De amplitudes zijn een maat voor de sterkte van het geluid. Welke amplitude heeft de grafiek die je bij b hebt gemaakt?


12. Twee trillingen hebben alleen een faseverschil. Als voor de ene trilling geldt `y_1 = sin(t)` dan geldt voor de andere `y_2 = sin(t - p)`. Een puntmassa trilt onder invloed van beide trillingen.
    1. Waarom trilt deze puntmassa zuiver harmonisch?
    2. Voor welke waarden van `p` trilt deze puntmassa met een amplitude van `2`?
    3. Voor welke waarden van `p` komt deze puntmassa niet in beweging?
    4. Voor welke waarden van `p` trilt de puntmassa met een amplitude van `1,5`?


13. Een passerend schip veroorzaakt op een rivier een golf die tegen de wal wordt teruggekaatst. Gedurende enige tijd ondervindt een klein vissersbootje zowel invloed van de oorspronkelijke golf als van de teruggekaatste golf. Bij de terugkaatsing wordt door demping de amplitude kleiner en wel `1/3` deel van de oorspronkelijke amplitude.
    De teruggekaatste golf is het spiegelbeeld van de voortzetting van de oorspronkelijke golf. Stel je voor dat de voor oorspronkelijke golf geldt `h(t) = sin(t)` met `t` in radialen. Verder bevindt de dichtstbijzijnde golftop zich `5/6` periode uit de wal.
    1. Toon nu aan dat voor de combinatie van beide golven geldt: `h(t) = sin(t) + 2/3 sin(t + 3 1/3pi)`.
    2. Toon aan dat de combinatie van beide golven een sinusoïde is.
    3. Welke amplitude heeft deze sinusoïde?

Testen

14. Een puntmassa beweegt onder invloed van twee zuiver harmonische trillingen. Laat door berekening zien in welk van de volgende gevallen de puntmassa zelf ook zuiver harmonisch trilt. Bepaal in die gevallen de frequentie en de amplitude van de trilling.
    1. `u_1 = 5 sin(t)` en `u_2 = 10 + 5 sin(t + 2)`
    2. `u_1 = 5 sin(t)` en `u_2 = 10 + 5 sin(2t)`
    3. `u_1 = 5 sin(220pi t)` en `u_2 = 10 + 3 sin(220pi t)`