
Goniometrische formules
Inleiding
Je hebt gezien dat goniometrische functies soms periodiek zijn, maar soms ook niet. En af en toe lijkt een op het oog lastige functie een zuivere sinusoïde als grafiek op te leveren. Om aan te tonen dat er dan ook echt van een sinusoïde sprake is, moet je het functievoorschrift kunnen herschrijven. En daarvoor heb je een aantal eigenschappen van sin, cos en tan nodig: de goniometrische formules.
Je leert nu:
- de goniometrische formules (symmetrieformules, somformules, verdubbelingsformules, enz.) kennen;
- hoe je de goniometrische formules uit elkaar kunt afleiden;
- de goniometrische formules gebruiken bij het herschrijven van functievoorschriften en het oplossen van vergelijkingen.
Je kunt al:
- werken met sinusoïden en vergelijkingen met sinus en cosinus oplossen;
- goniometrische functies met de grafische rekenmachine onderzoeken;
- werken met de functie y = tan(x).
Verkennen
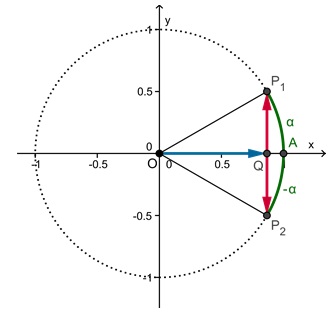
Om eigenschappen van sinus, cosinus en tangens af te leiden moet je kijken naar hun definities in de eenheidscirkel:
- sin(α) = yP
- cos(α) = xP
- tan(α) =
Hier zie je α en –α in één figuur.
> Leg uit waarom cos(α) = cos(–α).
> Welk verband is er tussen sin(α) en
sin(–α)?
> Kun je nog meer van dit soort symmetrieformules afleiden?
> Denk ook eens aan de stelling van Pythagoras.
Kun je iets zeggen over sin2(α) + cos2(α)?
Uitleg

Om eigenschappen van sinus, cosinus en tangens af te leiden moet je kijken naar hun definities in de eenheidscirkel:
- sin(α) = yP
- cos(α) = xP
- tan(α) =
In deze figuur zie je de hoeken α en β = π – α.
Omdat ΔOQP en ΔOQ'P' congruent zijn vanwege de symmetrie van de figuur geldt:
- sin(π – α) = sin(α)
- cos(π – α) = –cos(α)
- tan(π – α) = –tan(α)
Kijk je alleen naar ΔOQP dan zie je op grond van de stelling van Pythagoras:
sin2(α) + cos2(α) = 1
Op deze wijze kun je allerlei symmetrieformules voor sin, cos en tan afleiden.
Bijvoorbeeld: sin(–α) = –sin(α), cos(–α) = cos(α) en tan(–α) = –tan(α).
Of: sin(π – α) = cos(α) en cos(π – α) = sin(α).
Of: cos(α) = sin(α + π) en sin(α) = cos(α – π).
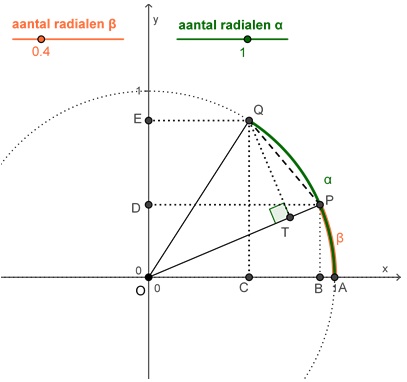
Met behulp van de figuur hiernaast kun je de zogenaamde somformules afleiden. Je ziet hoe hier de hoeken α en β "op elkaar gestapeld" zijn. Het is de bedoeling om sin(α + β) uit te drukken in sin(α), sin(β), cos(α) en cos(β) met behulp van rechthoek OQCD en de rechthoekige ΔOPR. Dit gaat alleen zolang α + β tussen 0 en 0,5π blijft. Alle andere situaties moet je met behulp van de symmetrieformules en de eenheidscirkel tot deze herleiden!
Ga na, dat sin(α + β) = .
Ga ook na, dat sin(α) = , cos(α) = ,
sin(β) = en cos(β) = .
Dan is:
sin(α) · cos(β) + cos(α) · sin(β) = · + · = + = = sin(α + β).
Hiermee heb je afgeleid: sin(α + β) = sin(α) · cos(β) + cos(α) · sin(β).
Met behulp van de symmetrieformules kun je hier dan weer varianten op maken.
En daarbij maak je de verdubbelingsformules en de formules van Simpson...
‡
Opgaven
-
Bekijk de symmetrieformules die in de Uitleg worden afgeleid.
- Laat nu zelf zien, dat: `sin(–alpha) = –sin(alpha)` en `cos(–alpha) = cos(alpha)` en `tan(-alpha) = - tan(alpha)`.
- Laat zien, dat: `sin(1/2 pi – alpha) = cos(alpha)` en `cos(1/2 pi – alpha) = sin(alpha)`.
- Laat ook zien dat: `cos(alpha) = sin(alpha + 1/2 pi)` en `sin(alpha) = cos(alpha – 1/2 pi)`.
-
Breng de grafiek van `y = sin^2(x) + cos^2(x)` op je grafische rekenmachine in beeld.
- Welke formule heb je nu zichtbaar gemaakt? En hoe wordt die formule in de Uitleg afgeleid?
- Maakt het daarbij verschil of je in graden of radialen werkt?
-
In de Uitleg wordt de formule `sin(alpha + beta) = sin(alpha)cos(beta) + cos(alpha)sin(beta)` afgeleid. Hieruit kun je formules afleiden voor `sin(alpha - beta)`, `cos(alpha + beta)` en `cos(alpha - beta)`.
Je ziet al die formules in de Theorie.
- Leid eerst de formule voor `sin(alpha - beta)` af. Gebruik de symmetrieformules.
- Leid nu de formule voor `cos(alpha + beta)` af. Gebruik daarbij formules die `sin` omzetten in `cos` en omgekeerd.
- Uit de formule bij b kun je een formule voor `cos(alpha - beta)` afleiden. Laat zien hoe.
- Leid een formule af voor `tan(alpha + beta)`. Zorg er voor dat er alleen de `tan` in voorkomt.
-
In de Uitleg worden ook de formules van Simpson genoemd. Eén van die formules is `sin(p) + sin(q) = 2 sin(1/2(p+q)) cos(1/2(p-q))`.
Deze formule kun je afleiden uit de formules voor `sin(alpha + beta)` en `sin(alpha - beta)`. Probeer dat zelf te doen, neem `alpha + beta = p` en `alpha - beta = q`.
Theorie
| Symmetrieformules | Somformules |
sin(–α) = –sin(α)
cos(–α) = cos(α)
tan(–α) = –tan(α)
sin(π – α) = sin(α)
cos(π – α) = –cos(α)
tan(π – α) = –tan(α)
|
sin(α + β) = sin(α) · cos(β) + cos(α) · sin(β)
sin(α – β) = sin(α) · cos(β) – cos(α) · sin(β)
cos(α + β) = cos(α) · cos(β) – sin(α) · sin(β)
cos(α – β) = cos(α) · cos(β) + sin(α) · sin(β)
|
| Verbanden tussen sin en cos |
sin(π – α) = cos(α)
cos(π – α) = sin(α)
sin2(α) + cos2(α) = 1
|
| Verdubbelingsformules | Formules van Simpson |
sin(2α) = 2 sin(α) cos(α)
cos(2α) = cos2(α) – sin2(α)
cos(2α) = 2 cos2(α) – 1
cos(2α) = 1 – 2 sin2(α)
|
sin(p) + sin(q) = 2 sin((p + q)) cos((p – q))
sin(p) – sin(q) = 2 sin((p – q)) cos((p + q))
cos(p) + cos(q) = 2 cos((p + q)) cos((p – q))
cos(p) – cos(q) = –2 sin((p + q)) sin((p – q))
|
Dit is een overzicht van de belangrijkste goniometrische formules.
Met behulp van de eenheidscirkel zijn de symmetrieformules, de verbanden tussen sin en cos en de eerste somformule af te leiden, zie de Uitleg. Uit deze formules kun je de rest herleiden...
‡
Voorbeeld 1
Toon aan dat de functie f met f(x) = sin(x) + cos(x) een sinusoïde is.
Antwoord
Je moet het functievoorschrift herschrijven tot f(x) = a sin(b(x – c)) + d (of zoiets met cos).
Daarvoor moeten sin(x) en cos(x) worden opgeteld.
Bij de goniometrsiche formules vind je alleen gevallen waarin twee sinussen of twee cosinussen worden opgeteld.
Daarom begin je met cos(x) = sin(π – x).
Je vindt: f(x) = sin(x) + sin(π – x).
En dit wordt met één van de formules van Simpson:
f(x) = 2 sin((x + (π – x)) cos((x – (π – x)) = 2 sin(π) cos(x – π) =
= cos(x – π).
En f(x) = cos(x – π) is een formule van een sinusoïde.
‡
Voorbeeld 2
Leid de verdubbelingsformules af uit de somformules.
Stel ook een vergelijkbare formule op voor tan(2x).
Antwoord
Neem sin(α + β) = sin(α) · cos(β) + cos(α) · sin(β).
Kies α = x en β = x.
Je vindt: sin(2x) = sin(x) cos(x) + sin(x) cos(x) = 2 sin(x) cos(x).
Neem cos(α + β) = cos(α) · cos(β) – sin(α) · sin(β).
Kies α = x en β = x.
Je vindt: cos(2x) = cos(x) cos(x) – sin(x) sin(x) = cos2(x) – sin2(x).
M.b.v. sin2(x) + cos2(x) = 1 kun je de twee andere formules voor cos(2x) uit de voorgaande afleiden.
tan(2x) = .
Deel je nu teller en noemer van deze breuk door cos2(x), dan krijg je:
tan(2x) = .
‡
Voorbeeld 3
Los op [–π,π] op: sin(2x) – sin(x) < 0.
Antwoord
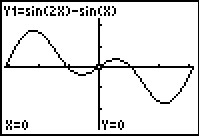 Je maakt eerst de grafiek van f(x) = sin(2x) – sin(x) op [–π,π].
Je maakt eerst de grafiek van f(x) = sin(2x) – sin(x) op [–π,π].
Vervolgens los je op: sin(2x) – sin(x) = 0.
Dit kun je op twee manieren doen:
-
Je gebruikt sin(2x) = 2 sin(x) cos(x).
Dan krijg je 2 sin(x) cos(x) – sin(x) = 0.
Ontbinden geeft: sin(x)(2 cos(x) – 1) = 0.
En zo vind je: sin(x) = 0 V cos(x) = 0,5.
Oplossingen: x = –π V x = –π V x = 0 V x = π V x = π.
-
Je kunt ook meteen de vergelijking schrijven als sin(2x) = sin(x).
Dan vind je: 2x = x + k · 2π V 2x = π – x + k · 2π.
Dit geeft: x = 0 + k · 2π V 3x = π + k · 2π en dus x = k · 2π V x = π + k · 2π.
Dit geeft op [–π,π] dezelfde vijf oplossingen.
De oplossing van de ongelijkheid wordt: –π < x < 0 V π < x < π.
‡
Voorbeeld 4
Gegeven is op [–2π,2π] de functie f met f(x) = cos(2x) – 2 cos(x).
Bereken de nulpunten van deze functie en los op: f(x) = –1.
Antwoord
Voor de nulpunten moet je oplossen f(x) = cos(2x) – 2 cos(x) = 0.
Hierbij maak je gebruik van cos(2x) = 2 cos2(x) – 1.
De vergelijking wordt dan: 2 cos2(x) – 1 – 2 cos(x) = 0.
Schrijf je dit als 2 cos2(x) – 2 cos(x) – 1 = 0, dan krijg je een kwadratische vergelijking in cos(x). Die kun je oplossen met de abc-formule:
cos(x) = .
Dit levert op: cos(x) = + V cos(x) = – .
Nu zijn benaderingen nodig, bijvoorbeeld in twee decimalen nauwkeurig:
cos(x) ≈ 1,366 V cos(x) ≈ –0,366.
Alleen cos(x) ≈ –0,366 heeft oplossingen, namelijk
x = arccos(–0,366) + k · 2π V x = –arccos(–0,366) + k · 2π.
Er zijn dus twee series nulpunten: (1,95 + k · 2π,0) en (–1,95 + k · 2π,0).
De vergelijking f(x) = cos(2x) – 2 cos(x) = –1 geeft op dezelfde manier:
2 cos2(x) – 1 – 2 cos(x) = –1 en dus 2 cos2(x) – 2 cos(x) = 0.
Ontbinden is nu mogelijk: 2 cos(x)(cos(x) – 1) = 0.
Je vindt daarom: cos(x) = 0 V cos(x) = 1.
En daarvan kun je gemakkelijk alle antwoorden opschrijven...
‡
Opgaven
-
Bekijk Voorbeeld 1. Er wordt aangetoond dat `f(x) = sin(x) + cos(x) = sqrt(2) cos(x - 1/4 pi)`. En dus is `f` een zuivere sinusoïde.
Los nu algebraïsch vergelijking `f(x) = 1` op.
-
Als je de sinusoïden `y_1 = sin(x)` en `y_2 = sin(x - 1/6 pi)` optelt, krijg je de functie `f(x) = sin(x) + sin(x - 1/6 pi)`.
Laat zien dat je het functievoorschrift van `f` zo kunt herleiden dat je er een zuivere sinusoïde in herkent.
-
In Voorbeeld 2 worden de verdubbelingsformules afgeleid.
- Leid alle drie de formules voor `cos(2x)` af die in de Theorie worden genoemd.
- Leid zelf de formule voor `tan(2x)` af.
-
In Voorbeeld 3 wordt de vergelijking `sin(2x) - sin(x) = 0` op twee manieren opgelost.
- Bij welke van beide manieren wordt gebruik gemaakt van symmetrie? Bij welke stap in de oplossing?
- Bij de andere methode wordt een verdubbelingsformule gebruikt. Bij welke stap in de oplossing?
-
Los algebraïsch op in `[0,2pi]`: `sin(2x) - cos(x) > 0`. Geef benaderingen in twee decimalen nauwkeurig.
-
In Voorbeeld 4 wordt de functie `f(x) = cos(2x) - 2 cos(x)` bekeken.
- Voer de berekening van de nulpunten van de grafiek van `f` zelf uit.
- Maak de oplossing van `f(x) = -1` verder af.
- Los in `[0,2pi]` op: `f(x) < -1`.
Verwerken
-
Als je de sinusoïden `y_1 = cos(x)` en `y_2 = cos(x + 1/4 pi)` van elkaar aftrekt, krijg je de grafiek van de functie `f(x) = cos(x) - cos(x + 1/4 pi)`.
- Toon aan dat `f` een sinusoïde is.
- Bereken met behulp van je formule bij a de toppen en de nulpunten van de grafiek van `f`.
- Los algebraïsch op `[0,2pi]` op: `f(x) > 1/2`. (Benaderingen in twee decimalen nauwkeurig.)
-
Met domein `[0,2pi]` is gegeven de functie `f(x) = sin^2(x) - 1/2 cos(x) - 1`.
- Bepaal de nulpunten van deze functie met de grafische rekenmachine.
- Laat zien dat je deze functie kunt herschrijven tot `f(x) = -cos^2(x) - 1/2 cos(x)`.
- Bereken nu de nulpunten exact.
- Los algebraïsch op: `f(x) > -1/2`.
-
Met domein `[0,2pi]` is gegeven de functie `f(x) = 1/8 tan(x) - sin(x)`.
- Bereken algebraïsch de nulpunten van deze functie.
- Breng de grafiek in beeld en bepaal de toppen.
- Welke asymptoten heeft de grafiek?
- Los algebraïsch op: `f(x) >= 1/2 sin(x)`.
-
Los de volgende vergelijkingen algebraïsch op.
- `sin(x + 2/3 pi) + sin(x) = 1/2`
- `cos(x + 1/3 pi) = cos(x)`
- `cos^2(x) + sin(x) = 1`
- `2 sin^2(x) - cos(2x) = 0`
- `2 cos^2(x) - 2 sin(x) = 0`
- `tan(x) = sin(x)`
-
Gegeven zijn de functies `f(x) = sin(x - 1/4 pi)`, `g(x) = sin(x + 1/4 pi)` en `S(x) = f(x) + g(x)`.
- Onderzoek met je grafische rekenmachine of de functie `S` een sinusoïde zou kunnen zijn.
- Toon algebraïsch aan dat `S` een sinusoïde is.
- Los algebraïsch op: `S(x) >= 1`.
Testen
-
Gegeven zijn de functies `y_1 = sin(2x) + 1/2`, `y_2 = sin(2x + 1/4 pi)` en `y_3 = y_2 - y_1`.
Neem voor al deze functies als domein `[-pi, pi]`.
- Toon aan dat de grafiek van `y_3` een zuivere sinusoïde is.
- Bepaal algebraïsch alle toppen en nulpunten van `y_3`.
- Los algebraïsch op: `y_3 >= 0`.
-
Los de volgende vergelijkingen algebraïsch op.
(Eventuele benaderingen in drie decimalen nauwkeurig.)
- `sin(x) = cos(x)`
- `sin(2x) = cos(x)`
- `cos^2(x) = sin^2(x)`
- `cos(x + 1/6 pi) + sin(x - 1/6 pi) = 1/2`
 Je maakt eerst de grafiek van f(x) = sin(2x) – sin(x) op [–π,π].
Je maakt eerst de grafiek van f(x) = sin(2x) – sin(x) op [–π,π].




