
Goniometrische functies

Inleiding
Muziek maak je door lucht in trilling te brengen. Dat doe je met een snaar, een holle buis, je stembanden, een trillend plaatje, e.d. Als je een snaar in trilling brengt hoor je behalve de grondtoon ook boventonen meeklinken. De frequenties van deze boventonen zijn een veelvoud van die van de grondtoon, maar ze klinken minder luid. Door de sinusoïden van de grondtoon en de boventonen op te tellen krijg je het trillingspatroon van de snaar.
Je leert nu:
- het begrip goniometrische functie;
- eigenschappen van dergelijke functies onderzoeken met de GR.
- de functie f(x) = tan(x) en zijn eigenschappen.
Je kunt al:
- werken met sinusoïden en vergelijkingen van de vorm sin(x) = a of sin(x) = a oplossen.
Verkennen
In de Westerse muziek worden zeven stamtonen onderscheiden, die samen een toonladder vormen. Deze zeven stamtonen worden aangeduid met A, B, C, D, E, F en G. De centrale A heeft een frequentie van 440 Hz (440 trillingen per seconde). Dit betekent dat in de lucht een trilling plaats vindt met die frequentie (is aantal trillingen per seconde).
Voor de A geldt dan bijvoorbeeld
u1(t) = a sin(440 · 2π · t).
De luidheid van deze grondtoon wordt bepaald door de amplitude a. Neem voor het gemak a = 1. De eerste boventoon van de A klinkt vaak minder luid, en dan geldt (bijvoorbeeld) u2(t) = 0,8 sin(880 · 2π · t).
Voor de tweede boventoon: u3(t) = 1,2 sin(1320 · 2π · t).
Tel je deze drie sinusfuncties op, dan krijg je een A met een bepaalde klankkleur.
> Breng eerst de grafiek van de grondtoon A maar eens in beeld met je grafische rekenmachine. Zorg dat je precies drie periodes in beeld krijgt.
> Zet de twee boventonen er bij en tel deze functies op.
> Is de resulterende snaartrilling een zuivere sinusoïde?
Uitleg
Je kent de functies f(x) = sin(x) en g(x) = cos(x) met x in radialen al. Omdat in deze functies de goniometrische verhoudingen sinus en cosinus voorkomen zijn het voorbeelden van goniometrische functies. De belangrijkste eigenschap is wel hun periodiciteit. Maar wat als je sin(x) en/of cos(x) gaat gebruiken om ingewikkelder functievoorschriften te maken? Bekijk eerst maar eens een paar grafieken:
- y3 = 1 + 2 sin(0,5x – 1)
- y4 = sin(x) + cos(x)
- y5 = sin(x2)
- y6 = sin2(x) = (sin(x))2
- y7 = sin(2x) – sin(x)
- y8 = x + sin(x)
Je weet dat y3 een zuivere sinusoïde is, dus daarbij is sprake van een periode (4π), een amplitude (2), een evenwichtsstand (y = 1) en een horizontale verschuiving (2 in de positieve x-richting). Ga dit na, eigenlijk moet je dit vooraf meteen kunnen zien.
Verder lijken ook y4 en y6 zuivere sinusoïden. Dat is ook inderdaad het geval, al kun je nu nog niet aantonen dat dit zo is. Je kunt wel periode, amplitude, evenwichtsstand en horizontale verschuiving uit de grafiek aflezen.
Van de overige functies is alleen y7 periodiek, de andere twee niet.
Zo kun je ook de tangens definiëren:
tan(α) = .
En dus geldt voor de tangensfunctie:
tan(x) = .
Deze functie is ook periodiek, maar nu met een periode van π.
Verder heeft deze functie verticale asymptoten: voor waarden van x waarbij cos(x) = 0 bestaan de functiewaarden niet, je deelt dan door 0. Dit is het geval als x = π + k · π.
‡
Opgaven
-
Gegeven is de goniometrische functie `f(x) = 12 + 4 sin(1/2 pi x - 1/4 pi)`.
- Breng de grafiek in beeld op de grafische rekenmachine. Waarom is het hierbij handig om vooraf in te zien dat het hier een sinuso´de betreft en de periode, de amplitude en de evenwichtsstand te bepalen?
- Welke horizontale verschuiving moet je op de grafiek van `y = sin(x)` toepassen om die van `f` te krijgen?
- Bereken de toppen van de grafiek van `f` op het interval `[0, 12]`.
- Los op: `f(x) <= 15`.
-
Ga van elk van de volgende functies na of de grafiek op een sinuso´de lijkt of niet.
- `y_1 = 1 + 2 sin(0,5x ľ 1)`
- `y_2 = sin(x) + cos(x)`
- `y_3 = sin(x^2)`
- `y_4 = sin^2(x) = (sin(x))^2`
- `y_5 = sin(9x) ľ sin(11x)`
-
Waarom weet je bij `y_2` en `y_3` eigenlijk (nog) niet zeker of hun grafieken echt dezelfde vorm hebben als die van `y = sin(x)`?
-
Bekijk de grafiek van `y = tan(x)` op je grafische rekenmachine.
- Breng die grafiek op je grafische rekenmachine zo in beeld, dat je precies twee periodes ziet.
- Waar zitten de verticale asymptoten van deze functie? Leg ook uit hoe je dat kunt afleiden uit de formule `tan(x) = (sin(x))/(cos(x))`.
- Voor welke waarden van `x` is `tan(x) = 1`?

Theorie
Onder goniometrische functies versta je functies waarin sin, cos (en tan) voorkomen.
De basisfuncties f(x) = sin(x) en
g(x) = cos(x) met x in radialen ken je al. De tangensfunctie is nieuw.
In deze eenheidscirkel zijn sinus, cosinus en tangens gedefinieerd als:
- sin(α) = yP
- cos(α) = xP
- tan(α) =
En dus geldt voor de tangensfunctie:
tan(x) = .
Deze functie is ook periodiek, maar nu met een periode van π.
Verder heeft deze functie verticale asymptoten: voor waarden van x waarbij cos(x) = 0 bestaan de functiewaarden niet, je deelt dan door 0. Dit is het geval als x = π + k · π.
De bekende sinusoïden zijn goniometrische functies die zuiver periodiek zijn en een amplitude en een evenwichtsstand hebben. Maar dat geldt niet voor alle goniometrische functies.
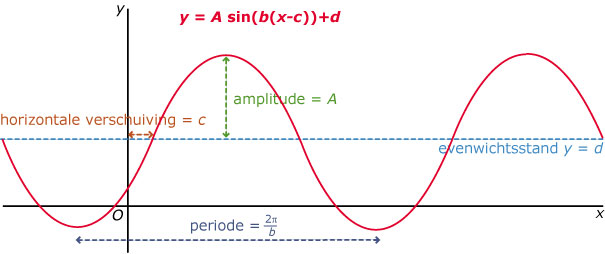
‡
Voorbeeld 1
Los op [–π,π] op: tan(x) ≤ 1.
Antwoord
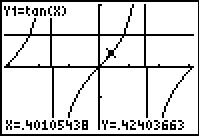
Maak eerst met je GR de grafiek van y = tan(x) op [–π,π].
De verticale asymptoten vallen meteen op. Omdat tan(x) = sin(x)/cos(x) vind je ze bij x-waarden waarvoor cos(x) = 0. Dus: x = π + k · π.
Los nu op: tan(x) = 1.
Omdat arctan(1) = π en de tangensfunctie een periode van π heeft, wordt dit:
x = π + k · π.
Uit de grafiek lees je nu de oplossing af, rekening houdend met de verticale asymptoten:
–π ≤ x < –π V –π < x ≤ π V π < x ≤ 2π
‡
Voorbeeld 2
Gegeven de functie f met voorschrift f(x) = 2 cos2(x) – 1.
(Met cos2(x) wordt (cos(x))2 bedoeld.)
Onderzoek of deze goniometrische functie periodiek is en bepaal dan de bijbehorende periode.
Antwoord
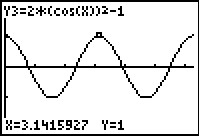
De standaard cosinusgrafiek heeft een periode van 2π. Het ligt dus voor de hand om de grafiek van f in beeld te brengen op bijvoorbeeld [0,2π]. Die grafiek lijkt op een zuivere sinusoïde met periode π, amplitude 1 en evenwichtsstand y = 0. Als je er een formule met cos bij wilt maken is de horizontale verschuiving 0.
Kortom: de grafiek lijkt op die van y = cos(2x).
Of dit echt het geval is, kun je (nog) niet aantonen.
Wel kun je de nulpunten berekenen en kijken of die hetzelfde zijn als die van y = cos(2x).
f(x) = 0 als 2 cos2(x) – 1 = 0, dus als cos(x) = – V cos(x) = .
Dit levert dezelfde waarden op als cos(2x) = 0 oplossen.
Ga dat zelf na.
‡
Voorbeeld 3
Gegeven de functie f met voorschrift f(x) = .
Is deze functie periodiek?
Bepaal de nulpunten en de asymptoten van deze functie.
Antwoord
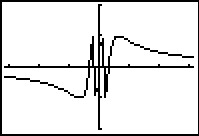 Omdat de standaard sinusfunctie een periode van 2π heeft en een vorm als 1/x juist voor x = 0 niet bestaat, bekijk je de grafiek op [–π,π]. Je krijgt dan op [–π,π]×[–2,2] de bovenste grafiek. In de buurt van x = 0 is erg onduidelijk hoe de grafiek er uit ziet, inzoomen laat zien dat er steeds meer en steeds smallere "golfjes" onstaan als je dichter bij 0 komt. Periodiek is hij in ieder geval niet...
Omdat de standaard sinusfunctie een periode van 2π heeft en een vorm als 1/x juist voor x = 0 niet bestaat, bekijk je de grafiek op [–π,π]. Je krijgt dan op [–π,π]×[–2,2] de bovenste grafiek. In de buurt van x = 0 is erg onduidelijk hoe de grafiek er uit ziet, inzoomen laat zien dat er steeds meer en steeds smallere "golfjes" onstaan als je dichter bij 0 komt. Periodiek is hij in ieder geval niet...
Nulwaarden: geeft = 0 + k · π en dus x = .
De positieve nulwaarden zijn , , , , enz.
Deze komen steeds dichter bij 0 te liggen en ook steeds dichter bij elkaar.
Voor de negatieve nulwaarden geldt iets vergelijkbaars.
Er is bij x = 0 geen verticale asymptoot omdat een sinus altijd binnen [–1,1] blijft.
Wel is er een horizontale asymptoot: als x heel groot (of heel groot negatief) wordt, dan nadert naar 0 en dus nadert ook f(x) naar 0.
De horizontale asymptoot is y = 0.
‡
Opgaven
-
Bekijk Voorbeeld 1. Los nu zelf op `[0,2pi]` op: `f(x) > sqrt(3)`.
-
Gegeven is de functie `f` met `f(x) = 10 sin(0,1pi(x - 5)) + 15` op het interval `[0,50]`.
- Lees periode, amplitude, evenwichtsstand en de horizontale verschuiving t.o.v. de `y`-as uit het functievoorschrift af.
- Teken de grafiek met je grafische rekenmachine.
- Los op in twee decimalen nauwkeurig: `f(x) = 12`.
-
Bekijk Voorbeeld 2.
- Breng zelf de grafiek van `f` op je grafische rekenmachine in beeld en bepaal de twee opeenvolgende maxima.
- Welke periode kun je hieruit afleiden voor de sinuso´de die lijkt te ontstaan?
- Welke andere formule zou je bij deze sinuso´de kunnen opstellen?
- Waarom weet je nog niet helemaal zeker dat de grafiek van `f` ook echt een sinuso´de is?
-
Gegeven de functie `f` met `f(x) = 2 sin(x) cos(x)` op `[0,2pi]`.
- Maak de grafiek van `f` op je grafische rekenmachine.
- Lijkt de grafiek op een sinuso´de? Zo ja, welke formule past er dan bij die sinuso´de?
- Los op: `f(x) = 0,5`. Geef benaderingen in twee decimalen nauwkeurig.
- Gebruik nu de formule van de sinuso´de die je bij b hebt gemaakt en los exact op: `y = 0,5`. Komen deze antwoorden overeen met die bij c?
-
Bekijk de grafiek van de functie `f(x) = 2x sin(x)` op `[0,2pi]`.
- Waarom kan hier geen sprake zijn van een sinuso´de?
- Is dit een periodieke functie?
- Beschrijf de regelmaat van de grafiek van `f`.
-
Bekijk eerst Voorbeeld 3. Je ziet daar een bijzondere functie die wel een sinus bevat maar niet periodiek is.
Gegeven is de functie `f` met `f(x) = sin(sqrt(x))`.
- Maak de grafiek van `f` op `[0,1000]`.
- Los op: `f(x) = 1`.
- Hoe kun je aan de antwoorden bij b zien dat dit geen periodieke functie is?
Verwerken
-
Als je de sinuso´den `y_1 = sin(x)` en `y_2 = cos(x)` optelt, krijg je de grafiek van de functie `f(x) = sin(x) + cos(x)`.
- Breng de grafiek in beeld op je grafische rekenmachine. Lijkt de grafiek op een sinuso´de? Waarom mag je op grond hiervan nog niet aannemen dat het er ook werkelijk ÚÚn is?
De grafiek van `f` is een sinuso´de.
- Geef de periode, de amplitude, de evenwichtsstand en de horizontale verschuiving ten opzichte van `y_1 = sin(x)`. Geef je antwoord in twee decimalen nauwkeurig.
- Stel een formule op voor deze sinuso´de.
- Bereken met behulp van je formule bij b de toppen en de nulpunten van de grafiek van `f`.
- Los op `[0,2pi]` op: `f(x) > 1`.
-
Bekijk de grafiek van de functie `g(x) = cos(x) - cos(2x)`.
- Deze grafiek is periodiek. Wat is de periode?
- Is de grafiek van `g` een sinuso´de?
- Bepaal met je grafische rekenmachine de nulpunten en de toppen van de functie `g`. Neem als domein `[0, 2pi]`.
-
De grafiek van de functie `y_2 = sin^2(x)` is een zuivere sinuso´de.
- Bepaal de periode, de amplitude, de evenwichtsstand en de horizontale verschuiving ten opzichte van de grafiek van `y = cos(x)`.
- Geef een passende formule voor deze sinuso´de.
- Los op: `y_2 = 1` door gebruik te maken van het oorspronkelijke functievoorschrift.
- Doe hetzelfde nog eens door gebruik te maken van de gevonden formule voor de sinuso´de.
-
Door de sinuso´den `y_1 = sin(x)` en `y_2 = sin(x - 1/6 pi)` op te tellen ontstaat de grafiek van een functie `f` . Neem voor het domein van `f` het interval `[0, 4pi]`.
- Breng de grafiek van `f` in beeld op je grafische rekenmachine.
- Neem aan dat de grafiek van `f` een zuivere sinuso´de is. Stel een formule op. Gebruik benaderingen in twee decimalen nauwkeurig.
- Los nu algebra´sch op: `f(x) < 0,5`.
-
Gegeven is de functie `f(x) = x sin(1/x)` met `[-0,5pi; 0,5pi]`.
- Breng de grafiek van `f` in beeld op je grafische rekenmachine.
- De grafiek ziet er in de buurt van de oorsprong nogal merkwaardig uit. Waardoor wordt dit veroorzaakt?
- Welke waarde zou je `f` geven voor `x = 0`?
- Hoe ziet de grafiek er uit als je heel ver van de oorsprong verwijderd bent? Probeer dat je verklaren.
Testen
-
Gegeven is de functie `f(x) = cos(x) - sin(x)`. De grafiek van `f` is een sinusoïde.
- Geef een formule voor deze sinusoïde met benaderingen in twee decimalen nauwkeurig.
- Bereken algebraïsch de nulpunten van `f`.
- Beredeneer de extremen van `f`.
- Los algebraïsch op: `f(x) >= 1`.
-
De toppen van `y = sin(x^2)` met domein `[-2pi, 2pi]` kun je met je grafische rekenmachine wel vinden. Je kunt ze ook algebra´sch bepalen. Laat zien hoe.
 Omdat de standaard sinusfunctie een periode van 2π heeft en een vorm als 1/x juist voor x = 0 niet bestaat, bekijk je de grafiek op [–π,π]. Je krijgt dan op [–π,π]×[–2,2] de bovenste grafiek. In de buurt van x = 0 is erg onduidelijk hoe de grafiek er uit ziet, inzoomen laat zien dat er steeds meer en steeds smallere "golfjes" onstaan als je dichter bij 0 komt. Periodiek is hij in ieder geval niet...
Omdat de standaard sinusfunctie een periode van 2π heeft en een vorm als 1/x juist voor x = 0 niet bestaat, bekijk je de grafiek op [–π,π]. Je krijgt dan op [–π,π]×[–2,2] de bovenste grafiek. In de buurt van x = 0 is erg onduidelijk hoe de grafiek er uit ziet, inzoomen laat zien dat er steeds meer en steeds smallere "golfjes" onstaan als je dichter bij 0 komt. Periodiek is hij in ieder geval niet...





