Totaalbeeld

Samenvatten

Je hebt nu alle theorie van "Veranderingen" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:
11: toenemende, afnemende of constante stijging of daling — extremen
12: toenamentabel — vaste stapgrootte — toenamendiagram
13: gemiddelde verandering — differentiequotiënt — koorde
14: veranderingssnelheid in een punt — differentiaalquotiënt — raaklijn
15: hellingsgrafiek — hellingsfunctie — tekenschema

Activiteitenlijst:
11: bij een functie (of grafiek) aangeven waar hij (toenemend, afnemend) stijgt en daalt;
12: bij een functie (of grafiek) een toenemediagram tekenen en omgekeerd bij een toenamediagram mogelijke grafieken van een bijpassende functie tekenen;
13: bij een functie (of grafiek) het differentiequotiënt op een gegeven interval berekenen en de betekenis daarvan omschrijven;
14: bij een functie (of grafiek) het differentiaalquotiënt voor een gegeven invoerwaarde berekenen en de betekenis ervan omschrijven — het hellingsgetal van een raaklijn aan een grafiek berekenen;
15: bij een functie (of grafiek) een hellingsgrafiek tekenen — uit een hellingsgrafiek eigenschappen van de functie (stijgen, dalen, extremen) aflezen.

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Veranderingen > Totaalbeeld > Achtergronden

Testen

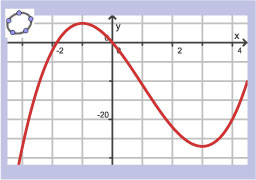  1. Je ziet hier een grafiek van de functie `f(x) = x^3 - 3x^2 - 9x`.
    1. Van welke soort daling is er sprake op het interval `[0;1]`?
    2. Bereken het differentiequotiënt op dit interval en beschrijf de betekenis van dit getal.
    3. Is de grafiek voor `x=1` stijgend of dalend?
    4. De helling van de grafiek voor `x=1` is het hellingsgetal van de raaklijn aan de grafiek in het bijbehorende punt. Bereken met behulp van een rij van differentiequotiënten dit hellingsgetal. Stel ook een vergelijking van de raaklijn op.
    5. Teken met behulp van je grafische rekenmachine een (benadering van de) hellingsgrafiek van de gegeven functie.
    6. Uit de hellingsgrafiek kun je de `x`-waarden van de extremen van de gegeven functie halen. Leg uit hoe en bereken de extremen van `f`.

  2. De hoogte van een vuurpijl die je van de grond afschiet wordt gegeven door `h(t) = 60t - 5t^2` waarin `h` de hoogte boven de begane grond in meter en `t` de tijd in seconden is na het afschieten.
    1. Na 10 seconden ontploft de vuurpijl. Hoe hoog is dat?
    2. Teken een bijpassend toenamediagram met stapgrootte 1.
    3. Uit het toenamediagram kun je aflezen op welk tijdstip de vuurpijl het hoogste punt in zijn baan bereikt. Leg uit hoe en bepaal de maximale hoogte van de vuurpijl.
    4. Bereken de gemiddelde snelheid van de vuurpijl over de eerste zes seconden.
    5. De snelheid van de vuurpijl neemt voortdurend af tot hij zijn hoogste punt heeft bereikt. Daar is de snelheid 0 m/s. Daarna neemt zijn snelheid weer toe. Bereken zijn snelheid op het moment van ontploffen
    6. De snelheid is afhankelijk van `t`. Maak met behulp van je grafische rekenmachine een grafiek van die snelheid.
    7. Als het goed is wordt je snelheidsgrafiek een rechte lijn. Stel bij die rechte snelheidsgrafiek een formule op. Bereken met die formule de snelheid op het moment van ontploffen.
    8. Welke formule geldt voor de snelheid van de vuurpijl?

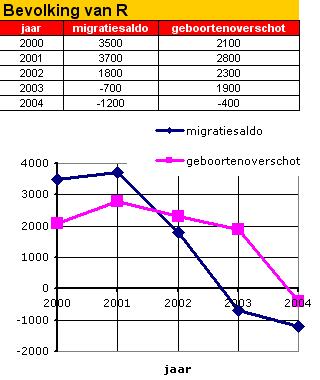  3. Het migratiesaldo van de grote stad R geeft het verschil tussen het aantal mensen dat in R komt wonen en het aantal mensen dat uit R vertrekt. Het geboorteoverschot is het verschil van het aantal geboorten en het aantal overledenen in R. In deze grafiek zie je beide voor de jaren 2000 tot en met 2004.
    1. Met hoeveel mensen is het aantal inwoners in R in het jaar 2000 toegenomen?
    2. In welk jaar is het aantal inwoners in deze stad afgenomen?
    3. Het aantal inwoners van R bedroeg aan het begin van het jaar 2000 ongeveer `72600` (op honderdtallen afgerond). Teken een grafiek van het aantal inwoners in R in de jaren 2000 tot en met 2004.
    4. Hoeveel was het aantal inwoners op 1 januari 2005?

Toepassen

  1. Een boer verbouwt suikerbieten op een bepaalde lap grond. Voor het onkruid wieden heeft hij personeel in dienst. De opbrengst bij de verkoop van de suikerbieten neemt toe als er beter wordt gewied, dus als hij meer werknemers in dienst neemt. Maar dat gaat niet onbeperkt: op zeker moment lopen de bietenwieders elkaar voor de voeten en wordt het wieden er niet beter van.

    Een mogelijk verband tussen de opbrengst `R` (in honderden euro) en het aantal werknemers `w` wordt gegeven door de formule `R=-1/3w^3 + 6w^2`.

    Voor de boer is het interessant om te weten hoeveel werknemers hij het beste kan inhuren. Daarbij kijkt hij naar de meeropbrengst van een werknemer. Zo is de meeropbrengst van de derde werknemer `R(3)-R(2)`. De meeropbrengst per werknemer heet in economentaal ook wel marginale opbrengst. De boer zorgt er voor dat hij zoveel werknemers in dienst neemt dat de marginale opbrengst van de laatste werknemer zo groot mogelijk is.
    1. Hoeveel bedraagt de marginale opbrengst (de meeropbrengst) van de derde werknemer?
    2. Je kunt met je grafische rekenmachine een tabel maken van de meeropbrengsten van elk van de eerste `10` werknemers. Maak die tabel en beslis op grond daarvan hoeveel werknemers de boer in dienst zal nemen voor het bieten wieden.
    3. De boer kiest voor zoveel werknemers, dat de meeropbrengst van de laatste werknemer zo groot mogelijk is. Waarom doet hij dat? Waarom kiest hij niet voor het aantal werknemers waarbij de opbrengst zo groot mogelijk is?

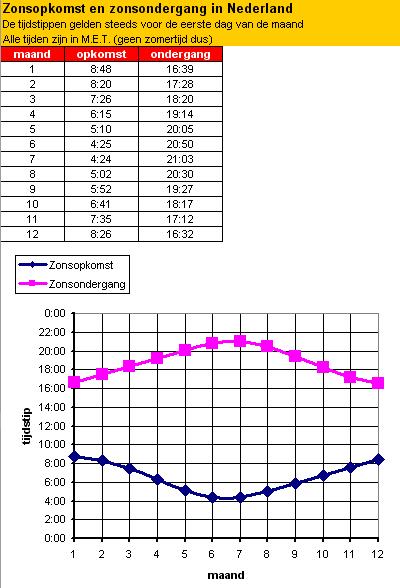  2. Door het KNMI worden de tijdstippen van zonsopkomst en zonsondergang gedurende het jaar bijgehouden. Via internet kun je actuele informatie over dit onderwerp vinden. Hier zie je een tabel en een grafiek voor Amsterdam in een bepaald jaar gemaakt in MS-Excel.

    Je ziet dat de tijdstippen van zonsopkomst en zonsondergang in de loop van het jaar veranderen. Bovendien is de snelheid waarmee die veranderingen plaatsvinden ook veranderlijk. In de tweede helft van de maand juni bijvoorbeeld verandert het tijdstip van zonsondergang maar weinig per dag. Maar in september is die verandering per dag juist behoorlijk groot. Ook de daglengte (verschil tussen zonsopkomst en zonsondergang) verandert in de loop van het jaar. En ook die verandering gaat soms sneller en soms minder snel...

    Een goede manier om de veranderingen nauwkeurig te bekijken is een toenamediagram bijvoorbeeld per maand.
    1. Het tijdstip van zonsopkomst verandert per dag. In welke maanden verandert het tijdstip van zonsopkomst het snelst per dag? Hoe zie je dat aan de grafiek?
    2. Ook het tijdstip van zonsondergang verandert per dag. Verandert het tijdstip van zonsondergang het snelst per dag in dezelfde maanden als dat van zonsopkomst? Kun je dit verklaren?
    3. De daglengte-grafiek is af te leiden uit die van zonsopkomst en zonsondergang. Hoe?
    4. In welke periode van het jaar wordt de daglengte in toenemende mate minder?
    5. Teken zelf in Excel een grafiek en een toenamediagram van de daglengte in de loop van het jaar. Neem de gegevens over. Neem voor het toenamediagram een stapgrootte van 1 maand.
    6. De daglengte verandert dagelijks. In welke maanden verandert de daglengte het snelst? Hoe zie je dat aan de grafiek en hoe aan het toenamediagram?
    7. In bepaalde maanden lijkt de daglengtewel vrijwel constant. Inwelke maanden is dat het geval? En hoe zie je dat aan het toenamediagram?
    8. In welke periode van het jaar wordt de daglengte in toenemende mate minder? Hoe zie je dat aan het toenamediagram?

  3. Voor de snelheid `v` in m/s van een bewegend voorwerp geldt: `v=2,4t` waarin `t` de tijd in seconden is.
    1. De grafiek van `v` is de hellingsgrafiek van de grafiek van de afgelegde weg `s(t)` waarin `s` in meters is uitgedrukt. Neem aan, dat `s(0)=0`. Maak een zo nauwkeurig mogelijke grafiek van `s(t)`.
    2. Bij de grafiek van `v(t)` hoort ook een hellingsgrafiek. Teken die hellingsgrafiek.
    3. Wat stelt de hellingsgrafiek van `v(t)` voor?
    4. Voor de afgelegde weg geldt de formule `s(t)=1,2t^2`
      Laat met behulp van het differentiequotiënt op het interval `[t,t + h]` zien, dat de gegeven functie `v` inderdaad de hellingsfunctie van `s` is.

  4. Gegeven is de functie `f(x)=0,25x^4`.
    Je kunt het differentiaalquotiënt voor `x=2` exact berekenen met behulp van het differentiequotiënt op het interval `[2,2 + h]`.
    Bereken dit differentiaalquotiënt.

  5. Gegeven is de functie `f(x)=x^3`.
    Toon aan dat `f'(x)=3x^2` met behulp van het differentiequotiënt op het interval `[x,x+h]`.

Examenopgaven

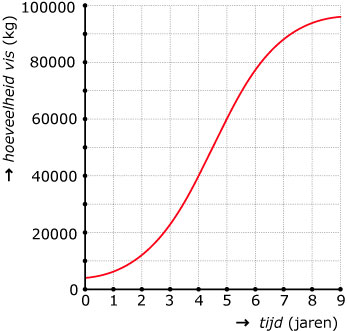  1. In een viskwekerij wordt vis uitgezet in een aantal nieuw aangelegde kweekvijvers. Als er geen vis wordt gevangen zal de visstand zich in de loop der jaren uitbreiden. De grafiek geeft een model van de groei van de visstand.
    1. Teken het toenamediagram voor intervallen van een jaar, te beginnen met het interval [1;2].
    2. De viskweker zal een aantal jaren afwachten alvorens te oogsten. Daarna wil hij jaarlijks dezelfde hoeveelheid vis vangen, liefst zoveel mogelijk. Het oogsten vindt steeds plaats aan het eind van het jaar. Na elke vangst breidt de visstand zich weer uit volgens de grafiek.
      Welk advies zou je de viskweker geven over:
      1. het aantal jaren dat hij na het uitzetten van de vis moet wachten;
      2. de grootte van de jaarlijkse vangst?
      Geef bij dit advies een toelichting waarmee je de viskweker denkt te overtuigen.

    (bron: examen wiskunde A vwo 1989, eerste tijdvak)