Totaalbeeld

Antwoorden bij de opgaven

    1. toenemende daling
    2. `(Delta y)/(Delta x) = (f(1) - f(0))/(1 - 0) = -11`
    3. dalend
    4. `f'(1)=-12` en `f(1)=-11`, dus de raaklijn heeft vergelijking `y=-12x+1`
    5. GR: Y1=X^3–3X^2–9X en Y2=(Y1(X+0.0001)–Y1(X))/0.0001
    6. Zoek de nulpunten van de hellingsfunctie. Je vindt: min.`f(3)=-27` en max.`f(-1)=5`.
    1. 100 m hoogte
    2. GR: Y1=60X–5X^2 en Y2=Y1(X)–Y1(X–1) geeft de toenametabel.
    3. Hoogste punt bij `t=6`. Bij `t=6` is nog sprake van toename t.o.v. de hoogte bij `t=5`, bij `t=7` is sprake van een afname t.o.v. de hoogte bij `t=6`. De maximale hoogte van de vuurpijl is 180 m.
    4. `180//6=30` m/s
    5. `h'(10)=-40` m/s
    6. GR: Y1=60X–5X^2 en Y2=(Y1(X+0.0001)–Y1(X))/0.0001
    7. `v(t)=60-10t`
    1. 5600 mensen
    2. In 2004
    3. De toenames zijn achtereenvolgens: 5600, 6500, 4100, 1200, -1600.
      De aantallen inwoners zijn daarom: 72600 (begin 2000), 78200 (begin 2001), 84700 (begin 2002), 88800 (begin 2003), 90000 (begin 2004) en 88400 (begin 2005)
    4. 88400 inwoners
    1. `23 2/3 xx 100` euro
    2. GR: Y1=-(1/3)X^3+6X^2 en Y2=Y1(X)–Y1(X-1)
      De boer zal 7 bietenwieders in dienst nemen.
    3. De 6e en de 7e bietenwieder hebben de hoogste meeropbrengst en brengen dus het meeste binnen tegen dezelfde loonkosten.
    1. september/oktober en maart/april; de grafiek is daar het steilst
    2. Ja in dezelfde maanden. Dit heeft te maken met de plaats van Nederland op Aarde en het feit dat de Aardas niet loodrecht staat op het vlak waarin de baan van de Aarde om de Zon ligt.
    3. Je neemt het verschil van het tijdstip van zonsopkomst en zonsondergang.
    4. -
    5. In dezelfde maanden als zonsopkomst en zonsondergang.
    6. In juni/juli en in december/januari. Toenames vrijwel 0.
    7. In augustus/september. Grote afnames (negatieve toenames).
    1. Het wordt de grafiek van `s(t) = 1,2t^2` als je uitgaat van een afgelegde weg van 0 op `t=0`.
    2. `v'(t)=2,4` want de grafiek van `v` is een rechte lijn met een richtingscoëfficiënt van 2,4.
    3. De versnelling.
  7. `(Delta y)/(Delta x) = (0,25(2+h)^4 - 0,25*2^4)/(2+h - 2) = 0,25*((4+4h+h^2)^2 - 16)/h = 8 + 6h + 2h^2 + h^3` en met `h rarr 0` vind je een differentiaalquotiënt van 8.
  8. `(Delta y)/(Delta x) = ((x+h)^3 - x^3)/(x+h - x) = 3x^2 + 3xh + h^2` en met `h rarr 0` vind je een differentiaalquotiënt van `f'(x)=3x^2`.
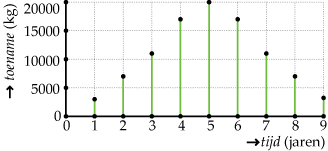
    2. In het vijfde jaar is de toename van het aantal kg vis het grootst (20000 kg).
      Als de viskweker 5 jaar wacht is er 60000 kg vis en hij kan dan jaarlijks 20000 kg vis vangen, precies de toename in dat vijfde jaar. Zo houdt hij steeds tussen de 40000 en de 60000 kg vis.