
Totaalbeeld
Samenvatten
Je hebt nu alle theorie van Periodieke functies doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!
Begrippenlijst:
61: periodiek verschijnsel — periode — golflengte — frequentie;
62: eenheidscirkel — draaihoek — radialen — standaardsinus;
63: arcsinus;
64: standaardcosinus — arccosinus;
65: sinusoïde — periode — amplitude — evenwichtslijn — horizontale verschuiving.
Activiteitenlijst:
61: bij een periodiek verschijnsel de periode, de golflengte en de frequentie bepalen;
62: draaihoeken omrekenen van graden naar radialen en omgekeerd — de standaard sinusgrafiek tekenen;
63: vergelijkingen met de standaardsinus oplossen, exact (met arcsin) en met de GR;
64: vergelijkingen bij de standaardcosinus oplossen, exact (met arccos) en met de GR;
65: bij een sinusoïde de periode, de amplitude, de evenwichtslijn en de horizontale verschuiving bepalen, zowel vanuit de grafiek als vanuit de formule — toppen en nulpunten van sinusoïden berekenen — vergelijkingen bij sinusoïden oplossen;
66: bij een gegeven periodiek verschijnsel een sinusoïde opstellen die dat verschijnsel zo goed mogelijk beschrijft.
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Achtergronden
Testen
-
Gegeven is de functie `f` door `f(x) = 200 - 50 * sin(1/2 x)` met `0 <= x <= 30`.
-
Bepaal het bereik van `f` en breng de grafiek van `f` in beeld op je grafische rekenmachine.
-
Los algebraïsch op: `f(x) <= 175`.
-
Los de volgende vergelijkingen algebraïsch op. Geef waar nodig benaderingen in twee decimalen nauwkeurig.
-
`25 + 10 cos((pi)/(7)(t - 15)) = 17`
-
`1 - 2 sin(2pi x) = 0`
-
Je ziet hier enkele sinusoïden. Geef telkens een bijpassend functievoorschrift.
I 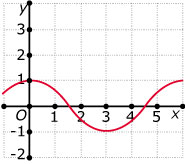 II
II 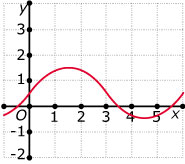 III
III 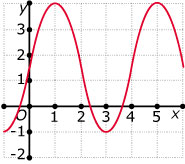
-
Bij het bepalen van de gewenste dijkhoogte langs de Nederlandse kust is het
belangrijk dat de dijk hoger is dan de te verwachten maximale waterhoogte bij een
stormvloed. De gemiddelde waterhoogte is daarbij niet van belang. Bij normale
omstandigheden kan de getijdenbeweging van het zeewater bij de Hondsbosse
zeewering te Petten redelijk worden beschreven door de functie:
`y = 0,4 + 1,5 sin(2pi/12,25 * t)`
met `t` in uren ten opzichte van middernacht op 21 juni 1998 en de waterhoogte `y`
in meters ten opzichte van het NAP.
Onder invloed van de stand van de zon en de maan kan de amplitude van de
getijdenbeweging variëren van 10% tot 140% van de amplitude van de gegeven
functie. Afhankelijk van de windsterkte, kan de gemiddelde waterhoogte bij
aanlandige wind 1,5 tot 2,5 meter hoger zijn dan normaal.
Hoe hoog moet de zeedijk van Petten volgens jou minimaal zijn? Licht je antwoord
toe aan de hand van het gegeven functievoorschrift.
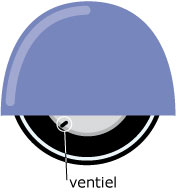 Van het autowiel in de figuur is slechts het onderste deel zichtbaar. Van de
wielhoogte is `3/4` deel afgeschermd achter het spatbord.
Van het autowiel in de figuur is slechts het onderste deel zichtbaar. Van de
wielhoogte is `3/4` deel afgeschermd achter het spatbord.
-
Hoeveel procent van de tijd is het ventiel zichtbaar als de auto met een constante snelheid rijdt?
-
"Zichtbaar" kun je aangeven met een 1, "onzichtbaar" met een 0. Je kunt dan de grafiek van de zichtbaarheid van het ventiel uitzetten tegen de tijd.
Is dit een periodieke functie? Zo ja, teken een periode op schaal.
Toepassen
Daglengte
De tijdstippen van zonsopkomst en zonsondergang variëren per dag. Lees hierover in
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Toepassingen
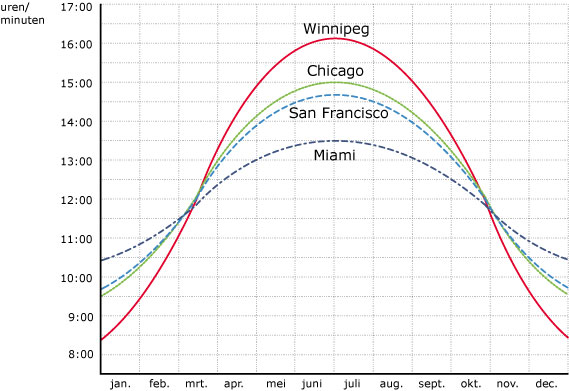
De volgende grafieken geven de daglengte in vier Amerikaanse steden. Ga er van uit dat deze grafieken zuivere sinusoïden zijn.
-
Stel voor de vier steden een voorschrift op voor de daglengte als functie van de tijd t in dagen; t = 0 op 1 januari.
-
Op welke datum is de langste dag van het jaar? En de kortste?
-
Hoeveel dagen per jaar is de daglengte meer dan 14 uur?
De manen van Jupiter
In 1610 werden de vier helderste Jupitermanen ontdekt door Galileï. De manen beschrijven bij benadering cirkelvormige banen om Jupiter, alle vier in dezelfde omlooprichting
Deze banen liggen (vrijwel) in één vlak met Jupiter en de Aarde. Daarom zie je Jupiter en de vier manen in een kijker altijd op één horizontale lijn liggen.
De onderlinge posities van de manen in het kijkerbeeld veranderen voortdurend.
Voor amateurastronomen worden maandelijks grafieken gepubliceerd waaruit ze op ieder moment de posities van de manen kunnen aflezen. Zie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Toepassingen
Het diagram op de website geeft informatie over de maand september in 2008.
Op 1 september 2008 om 0:00 uur waren dus van links (west) naar rechts (oost) in de kijker te zien:
Io (I, voor Jupiter), Europa (II), Ganymedes (III) en Callisto (IV).
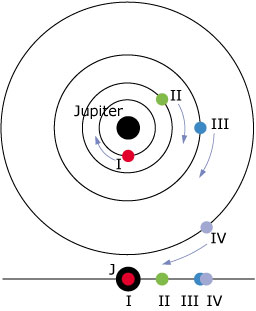
Hier zie je van de vier manen de posities op hum cirkelbanen op 1 januari 1990 om 0:00 uur getekend.
-
Teken in de figuur voor deze vier manen het deel van de baan dat ze doorlopen van 1 september 0:00 uur tot 5 september 0:00 uur.
In de kijker zie je de beweging van elk van die manen als een in de tijd veranderende uitwijking `u(t)` t.o.v. Jupiter op een horizontale as.
Die uitwijking kan goed worden beschreven met een sinuoïde. `u` wordt uitgedrukt in veelvouden van de straal van Jupiter en `t` is in dagen.
-
Voor Callisto geldt bij goede benadering `u(t) = 26 sin(0,365(t - 24))`. (Hierbij is er van uit gegaan dat "West" een positieve waarde van `u` betekent en "Oost" een negatieve.)
Laat zien dat deze formule redelijk overeenkomt met de gegeven grafiek. Bereken met de formule de omlooptijd van Callisto.
-
Stel zelf zo'n formule op voor Ganymedes.
-
De manen zijn in de figuur naar verhouding veel te groot getekend. In werkelijkheid zijn het stipjes. Dus als `-1 <= u(t) <= 1` dan kunnen de manen achter Jupiter zitten.
Bereken met behulp van de formule voor Ganymedes hoe lang deze maan achter Jupiter zit.
Fietsen
 Bij normaal weer, zonder al te veel mee- of tegenwind, legt een fietser gemiddeld 15 kilometer per uur af.
Als je bij een constante snelheid de hoogte van de trappers uitzet tegen de tijd, of de hoogte van het ventiel tegen de tijd, krijg je een mooie sinusoïden.
Bij normaal weer, zonder al te veel mee- of tegenwind, legt een fietser gemiddeld 15 kilometer per uur af.
Als je bij een constante snelheid de hoogte van de trappers uitzet tegen de tijd, of de hoogte van het ventiel tegen de tijd, krijg je een mooie sinusoïden.
-
Maak daarvan een overzicht met grafieken en formules. Geef redelijke schattingen van de bijbehorende afmetingen.
De baan die het ventiel aflegt als je fietst is geen sinusoïde.
-
Waarom is dat zo?
-
Hoe ziet die baan er dan wel uit? Maak er een zo goed mogelijke tekening van en verwerk die in het overzicht.
Examenopgaven
Bioritme
Op een pagina op Internet staat te lezen dat ons leven beheerst wordt door een drietal toestanden, namelijk door onze fysieke, onze emotionele en onze intellectuele toestand. Op de ene dag voel je je fysiek (lichamelijk) beter dan op een andere dag. Deze "fysieke toestand" kunnen we weergeven op een schaal van `–50` (fysiek op dieptepunt) tot `+50` (fysiek opperbest). Deze fysieke toestand varieert in de tijd volgens een sinusoïde.
Ook de "emotionele toestand" en de "intellectuele toestand" variëren op een schaal van `–50` tot `+50` volgens een sinusoïde. Zie figuur.

Bij de geboorte van een mens zou elke cyclus zich in dezelfde begintoestand bevinden, zoals is weergegeven in de figuur.
Tezamen bepalen de drie cycli het zogenaamde bioritme van een mens. Sommigen beweren dat het bioritme volledig vastlegt tot welke prestaties een mens op een bepaald moment in staat is. Zo zou je bijvoorbeeld kunnen uitrekenen op welke dag je het best kunt solliciteren.
Voor de fysieke cyclus is de periode 23 dagen, voor de emotionele cyclus 28 dagen en voor de intellectuele cyclus is de periode 33 dagen.
-
Het bioritme in de figuur betreft een pasgeboren baby. `E` is de emotionele toestand van de baby `t` dagen na de geboorte.
Hierbij hoort een formule van de vorm `E = a sin(bt)`. Geef de waarden van `a` en `b`.
-
Zodra de emotionele toestand beneden `–25` komt, zou het moeilijker worden om de emoties onder controle te houden.
Hoeveel procent van een periode heeft de emotionele toestand een waarde die kleiner is dan `–25`? Licht je antwoord toe.
-
`F` is de fysieke toestand van de baby. Onderzoek of `F` op de eerste verjaardag een dalend of een stijgend verloop heeft.
-
Annelies is op 1 januari 1983 geboren. Op 1 januari 2001 wordt ze dus 18 jaar. Vanaf die dag mag ze rijexamen doen.
Ze wil dat doen op een dag waarop zowel haar fysieke als haar intellectuele toestand positief is.
(De jaren 1984, 1988, 1992, 1996 en 2000 hebben een dag extra, dus 366 dagen.)
Onderzoek welke de eerste drie dagen van januari 2001 zijn die voor het rijexamen in aanmerking komen.
(bron: examen wiskunde B1,2 havo 2000, eerste tijdvak, opgave 1)
 |
 |
Golfplaat
Golfplaat is een bouwmateriaal dat gebruikt wordt voor het afdekken van eenvoudige bouwwerken.
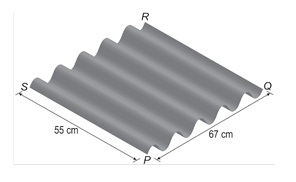
In de figuur hiernaast is een rechthoekig stuk golfplaat getekend.
Hieronder is het vooraanzicht van dit stuk golfplaat in een assenstelsel getekend. Hierbij is de dikte verwaarloosd.
In het assenstelsel zijn `x` en `y` uitgedrukt in cm. Bij deze grafiek behoort de formule:
`y = 3 + 3 sin(0,469x)`

De golfplaat wordt als afdakje gebruikt. De plaat wordt horizontaal neergelegd en steunt aan de randen `PQ` en `RS` op een muur.
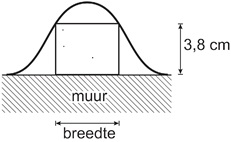
De ruimtes tussen de bovenrand van de muur en de golfplaat worden afgedicht met houten blokjes.
Deze blokjes zijn 3,8 cm hoog en hebben een zo groot mogelijke breedte. In figuur is dit geschetst.
-
Bereken de breedte van zo'n blokje. Geef je antwoord in mm nauwkeurig.
Het bovenaanzicht van het stuk golfplaat de figuur rechtsboven is een rechthoek `PQRS`. `PQ = 67` cm en `PS = 55` cm.
Dit stuk golfplaat wordt diagonaal doorgezaagd. In het bovenaanzicht is de zaagsnede een rechte lijn van `S` naar `Q`. De werkelijke vorm van de doorsnede is een sinusoïde.
-
Stel een formule op van deze sinusoïde als deze op ware grootte in een assenstelsel zoals in het vooraanzicht wordt weergegeven.
(bron: examen wiskunde B1,2 havo 2005, tweede tijdvak, opgave 5)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Achtergronden  II
II  III
III 
 Van het autowiel in de figuur is slechts het onderste deel zichtbaar. Van de
wielhoogte is `3/4` deel afgeschermd achter het spatbord.
Van het autowiel in de figuur is slechts het onderste deel zichtbaar. Van de
wielhoogte is `3/4` deel afgeschermd achter het spatbord.
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Toepassingen

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Totaalbeeld > Toepassingen

 Bij normaal weer, zonder al te veel mee- of tegenwind, legt een fietser gemiddeld 15 kilometer per uur af.
Als je bij een constante snelheid de hoogte van de trappers uitzet tegen de tijd, of de hoogte van het ventiel tegen de tijd, krijg je een mooie sinusoïden.
Bij normaal weer, zonder al te veel mee- of tegenwind, legt een fietser gemiddeld 15 kilometer per uur af.
Als je bij een constante snelheid de hoogte van de trappers uitzet tegen de tijd, of de hoogte van het ventiel tegen de tijd, krijg je een mooie sinusoïden.



