Totaalbeeld

Antwoorden bij de opgaven

    1. `text(B)_(f) = [150, 250]`
      Venster: `[0,30]xx[150,250]`.
    2. `f(x) = 175` geeft `sin(1/2 x) = 1/2` en `x = 1/3pi + k * 4pi vv x = 1 2/3 pi + k * 4pi`.
      De oplossing van de ongelijkheid wordt: `1/3 pi <= x <= 1 2/3pi vv 4 1/3 pi <= x <= 5 2/3pi vv 8 1/3 pi <= x <= 9 2/3pi`.
    1. `cos((pi)/(7)(t - 15)) = -0,8` geeft `(pi)/(7)(t - 15) = arccos(0,8) + k * 2pi vv (pi)/(7)(t - 15) = - arccos(0,8) + k * 2pi`.
      Dit levert op `t ~~ 9,43 + k * 14 vv t ~~ 20,57 + k * 14`.
    2. `sin(2pi x) = 0,5` geeft `2pi x = 1/6pi + k * 2pi vv 2pi x = 5/6pi + k * 2p` en dus `x = 1/12 + k vv x = 5/12 + k`.
  3. I: `y = cos((2pi)/6 x)`
    II: `y = 0,5 + sin((2pi)/6 x)`
    III: `y = 1,5 + 2,5sin((2pi)/4 x)`
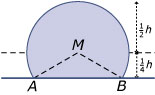
  4. Amplitude loopt van 0,15 tot 2,10 en evenwichtsstand kan oplopen tot 2,5 m. De dijk zou dus een hoogte van `2,10 + 2,50 = 4,60` m moeten hebben.
    1. Zie figuur. `/_AMB = 120^o` en dus is boog `AB` éénderde deel van de hele cirkel. Dus 33%.
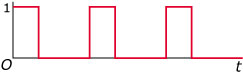
    2. Zie figuur, dit is een periodieke grafiek.

    1. Kies voor sinus-vorm. Het beginpunt 1 april is `t = 91`.
      Miami: `l(t) = 12 + 1,5 sin((2pi)/365 (t - 91))`
      San Francisco: `l(t) = 12,25 + 2,5 sin((2pi)/365 (t - 91))`
      Chicago: `l(t) = 12,25 + 2,75 sin((2pi)/365 (t - 91))`
      Winnipeg: `l(t) = 12,25 + 3,75 sin((2pi)/365 (t - 91))`
    2. 1 juli de langste en 1 januari de kortste dag.
    3. Miami: 0
      San Francisco: 110
      Chicago: 140
      Winnipeg: 160
    1. Zie figuur.
    2. Omlooptijd Callisto is `(2pi)/(0,365) ~~ 17,2` dagen.
    3. Ganymedes: `u(t) = 15 sin(0,85(t - 10))`
    4. Ganymedes zit achter Jupiter als hij van west naar oost beweegt en `-1 <= u(t) <= 1`.
      `u(t) = 1` geeft `t ~~ 10,1 + k * 7,4 vv t ~~ 13,6 + k * 7,4`.
      `u(t) = -1` geeft `t ~~ 9,9 + k * 7,4 vv t ~~ 13,8 + k * 7,4`.
      Ganymedes gaat achter Jupiter op bijvoorbeeld `t ~~ 13,6` en komt er dan weer achter weg op `t ~~ 13,8`.
      Ganymedes zit dus ongeveer 0,2 dagen achter Jupiter.
    1. Ventiel beweegt tussen 5 cm en 85 cm (schatting wieldiameter 0,9 m) en draait `15000/(0,9pi) ~~ 5305` keer per uur rond, dat is ongeveer 1,5 keer per seconde. De omwentelingstijd (periode) is daarom ongeveer `2/3` seconde.
      Mogelijke formule: `h(t) = 0,45 + 0,4 sin(3pi t)` met `t` in seconden, `h` in meter en op `t = 0` zit het ventiel op 45 cm hoogte en gaat het omhoog bewegen.
      Verzin zo ook een mooie formule voor een trapper.
    2. De hoogte hangt dan af van de afgelegde afstand.
    3. De baan wordt een cycloïde. Zoek maar eens op hoe die er uit ziet.
    1. `a = 50` en `b = (2pi)/8 ~~ 0,2244`
    2. `sin x = –1/2` geeft in de eerste periode `x = 7/6pi` of `x = 11/6pi`.
      `(11/6pi - 7/6pi)/(2pi) = 1/3` dus 33% van de periode
    3. Bij de fysieke toestand hoort de formule `F = 50 sin((2pi)/23 t)`.
      De fysieke toestand heeft op de eerste verjaardag een stijgend verloop. Dit is bijvoorbeeld te zien aan de grafiek of de tabel van de functie of van de hellingfunctie bij een domein rond 365 dagen.
    4. De formules `F = 50 sin((2pi)/23 t)` en `I = 50 sin((2pi)/33 t)` in de GR invoeren.
      De GR instellen op een domein vanaf (bijvoorbeeld) 6570 dagen en op de GR de bij `F` en `I` horende grafieken of tabellen raadplegen. De 6579e, 6580e en 6581e dag zijn geschikt, dus het antwoord is: de 5e, 6e en 7e januari 2001.
    1. `y = 3 + 3sin(0,469x) = 3,8` geeft `x ~~ 0,58 vv x ~~ 6,12`.
      De breedte van het blokje is ongeveer `6,12 - 0,58 = 0,55` cm (of 55 mm).
    2. De amplitude van de sinusoïde is 3.
      Van P naar Q is 5 perioden en van S naar Q is ook 5 perioden. `SQ = sqrt(SR^2 + RQ^2) = sqrt(67^2 + 55^2) ~~ 86,7`.
      De periode van de gevraagde sinusoïde is ongeveer `86,7/5 ~~ 17,35` cm.
      Een passende formule is `y = 3 + 3sin((2pi)/(17,35)x)`.