Sinusfuncties

Inleiding

Met periodieke functies kun je, door de herhaling, gemakkelijk voorspellingen doen. Dezelfde uitkomsten komen met een vaste regelmaat weer terug. Dit bemoeilijkt echter het terugrekenen. Zelfs een eenvoudige vergelijking als sin(x) = 0,5 heeft in principe oneindig veel oplossingen. Hoe vind je die allemaal en en hoe schrijf je ze allemaal netjes op? Daarover gaat dit onderdeel. Bij de grafiek van y = sin(x) neem je x altijd in radialen.

Je leert nu:

• de grafiek van y = sin(x) tekenen met x in radialen;
• de vergelijking sin(x) = c oplossen als c een constante is.

Je kunt al:

• een grafiek tekenen op de grafische rekenmachine en dan uit de grafiek x vinden, als y gegeven is;
• symmetrie in grafieken gebruiken.

Verkennen

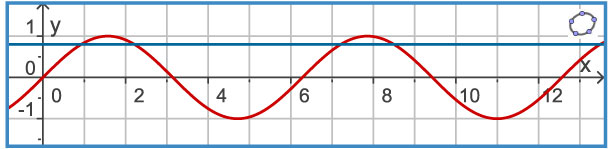
Gebruik deze grafiek van f(x) = sin(x) en de symmetrie ervan.

> Los op: sin(x) = 0,8 met $x\in [\mathrm{0,4}\pi ]$. Geef je antwoord in drie decimalen nauwkeurig.
> Los op: sin(x) = 0,8 met $x\in ℝ$ . Geef je antwoord in drie decimalen nauwkeurig.
> Los op: sin(x) = –0,5 met $x\in [\mathrm{0,4}\pi ]$. Geef je antwoord exact.
> Los op: sin(x) = –0,5 met $x\in ℝ$. Geef je antwoord exact.

Uitleg

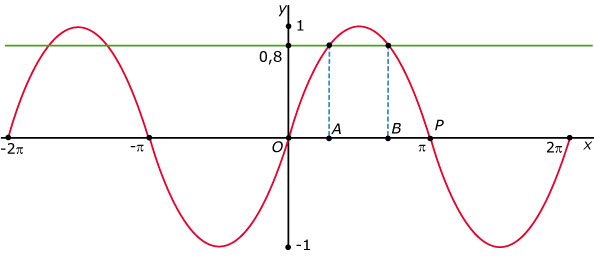
Hier kun je zien hoeveel oplossingen de vergelijking sin(x) = c heeft als c een constante is. Je gebruikt daarbij de symmetrie en de periode van de grafiek van y = sin(x).

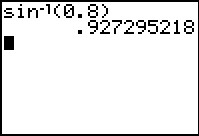Als je bijvoorbeeld sin(x) = 0,8 wilt oplossen, bepaal je eerst de oplossing die zo dicht mogelijk bij de verticale as zit: x ≈ 0,93.
Dit getal kun je vinden met je grafische rekenmachine.
Het heet in de wiskunde de arcussinus van 0,8: x = arcsin(0,8) ≈ 0,93.
Binnen één periode is (vaak) nog een oplossing.
Vanwege de symmetrie van de grafiek is die tweede oplossing x = π – arcsin(0,8).

Vanwege de periode van 2π zijn alle oplossingen van deze vergelijking:
x = arcsin(0,8) + k · 2π  V  x = π – arcsin(0,8) + k · 2π   met k een geheel getal.

Door c te veranderen kun je de oplossingen zien van andere vergelijkingen zoals bijvoorbeeld
sin(x) = 0,2 en sin(x) = –0,2 enzovoorts...

Je ziet bovendien:

• sin(x) = 1 heeft als oplossingen: x = 0,5π + k · 2π
• sin(x) = –1 heeft als oplossingen: x = –0,5π + k · 2π
• sin(x) = 0 heeft als oplossingen: x = 0 + k · π = k · π
• Als c groter dan 1 of kleiner dan –1 is zijn er geen oplossingen.

‡

Opgaven

1. Bekijk de Uitleg. Los nu zelf op:
   1. `sin(x) = 0,2`
   2. `sin(x) = -0,2`


2. Waarom heeft `sin(x) = 1,2` geen oplossingen?
   

Theorie

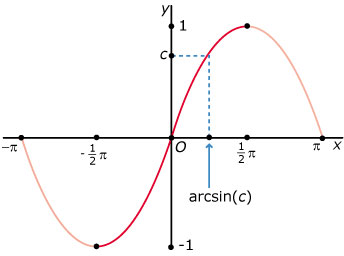
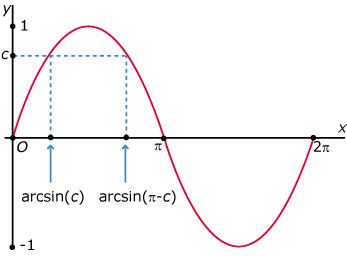
Je ziet hier de grafiek van f(x) = sin(x) met x in radialen op `[0,2pi]`. Verder zijn de oplossingen van sin(x) = c aangegeven (c is een constante).

De oplossing van sin(x) = c die ligt binnen $[-\frac{1}{2}\pi ,\frac{1}{2}\pi ]$  heet de arcussinus van c: x = arcsin(c).
Binnen één periode is (vaak) nog een oplossing.
Vanwege de symmetrie van de grafiek is die tweede oplossing x = π – arcsin(c).

Vanwege de periode van 2π zijn alle oplossingen van sin(x) = c:
x = arcsin(c) + k · 2π  V  x = π – arcsin(c) + k · 2π   met k een geheel getal.

De vergelijking sin(x) = c heeft alleen oplossingen als $-1\le c\le 1$.

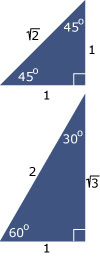
Er zijn enkele waarden die handig zijn om te gebruiken:

• sin(0) = 0
• sin($\frac{1}{6}\pi$) = 0,5
• sin($\frac{1}{4}\pi$) = $\frac{1}{2}\sqrt{2}$
• sin($\frac{1}{3}\pi$) = $\frac{1}{2}\sqrt{3}$
• sin($\frac{1}{2}\pi$) = 1

en omgekeerd:

• arcsin(0) = 0
• arcsin(0,5) = $\frac{1}{6}\pi$
• arcsin($\frac{1}{2}\sqrt{2}$) = $\frac{1}{4}\pi$
• arcsin($\frac{1}{2}\sqrt{3}$) = $\frac{1}{3}\pi$
• arcsin(1) = $\frac{1}{2}\pi$

Worden er exacte uitkomsten gevraagd, dan gebruik je deze waarden.

‡

Voorbeeld 1

Los op: sin(x) = 0,5 met x in [0,3π].

Antwoord

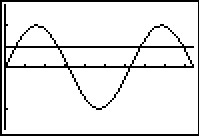Maak eerst met je grafische rekenmachine de grafieken van y₁ = sin(x) en y₂ = 0,5 op het gegeven interval.

Een oplossing is: arcsin(0,5).
Met je rekenmachine geeft dat in drie decimalen nauwkeurig: x ≈ 0,524.

Op het gewenste interval vind je dan vier oplossingen:
x ≈ 0,524  V  x ≈ π – 0,524  V  x ≈ 2π + 0,524  V  x ≈ 3π – 0,524.
En dus: x ≈ 0,524  V  x ≈ 2,618  V  x ≈ 6,807  V  x ≈ 8,901.

Het exacte antwoord is: x = $\frac{1}{6}\pi$ (zie de tabel bij de theorie).

Op het gegeven interval: x ≈ $\frac{1}{6}\pi$  V  x ≈ π – $\frac{1}{6}\pi$  V  x ≈ 2π + $\frac{1}{6}\pi$  V  x ≈ 3π – $\frac{1}{6}\pi$.
En dus: x = $\frac{1}{6}\pi$  V  x = $\frac{5}{6}\pi$  V  x = $2\frac{1}{6}\pi$  V  x = $2\frac{5}{6}\pi$.

‡

Voorbeeld 2

Los op: sin(x) = –0,8.

Antwoord

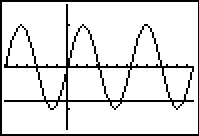Bekijk een deel van de standaard sinusgrafiek en zet er de lijn y₂ = –0,8 bij in. Zorg dat in ieder geval een hele periode zichtbaar is.

Een oplossing is: x = arcsin(–0,8) ≈ –0,927 (een exacte uitkomst is er niet).
De tweede oplossing binnen een periode is: x = π – –0,927 ≈ 4,069.

Alle verdere oplossingen zijn nu te vinden door bij deze twee oplossingen een veelvoud van de periode op te tellen:
x ≈0,927 + k · 2π  V  x ≈ 4,069 + k · 2π   met k een wilekeurig geheel getal.

‡

Voorbeeld 3

Los op: 3 · sin(x) + 1 < 0.

Antwoord

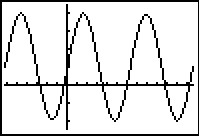Je kunt de grafiek van de functie f(x) = 3 · sin(x) + 1 bekijken met je grafische rekenmachine. Het gaat bij de vergelijking 3 · sin(x) + 1 = 0 om de nulwaarden van deze functie, dat zijn er oneindig veel.

De vergelijking 3 · sin(x) + 1 = 0 herschrijf je tot sin(x) = –$\frac{1}{3}$.

De oplossingen hiervan zijn: x = arcsin(–$\frac{1}{3}$) + k · 2π  V  x = π – arcsin(–$\frac{1}{3}$) + k · 2π.
In drie decimalen nauwkeurig: x = –0,340 + k · 2π  V  x = 3,841 + k · 2π.

In de grafiek zie je dat de functiewaarden negatief zijn als x tussen 3,841 en –0,340 + 2π inligt, dus voor 3,841 < x < 5,943.
De oplossing van de ongelijkheid is nu: 3,841 + k · 2π < x < 5,943 + k · 2π.

‡

Opgaven

3. Bekijk Voorbeeld 1.
   Los nu op `sin(x) = -0,5`.
   1. Geef alle oplossingen benaderd in drie decimalen nauwkeurig.
   2. Geef alle exacte oplossingen.
   3. Geef alle exacte oplossingen op het interval `[0,4pi]`.


4. Bekijk de grafiek van `f(x) = sin(x)`. Zorg dat je in ieder geval één complete periode in beeld hebt.
   1. Los exact op: `sin(x) = 1/2 sqrt(2)`.
   2. Geef alle exacte oplossingen op het interval `[-2pi,4pi]`.
   3. Geef de oplossingen op het interval `[-2pi,4pi]` in drie decimalen nauwkeurig.


5. In Voorbeeld 2 los je `sin(x) = -0,8` op. Nu zijn alleen benaderingen mogelijk.
   1. Los op `sin(x) = 0,6` op het interval `[-pi,3pi]`. Geef benaderingen in twee decimalen nauwkeurig.
   2. Los op `sin(x) < 0,6` op het interval `[-pi,3pi]`. Geef benaderingen in twee decimalen nauwkeurig.
   3. Los op `sin(x) < -0,6` op het interval `[-pi,3pi]`. Geef benaderingen in twee decimalen nauwkeurig.


6. Bestudeer Voorbeeld 3. Je werkt daarin met de grafiek van de functie `f(x) = 3 sin(x) + 1`.
   1. Breng zelf deze grafiek in beeld op `[-2pi,4pi]`.
   2. Los `f(x) < 2` op met benaderingen in twee decimalen nauwkeurig.
   3. Los `f(x) = 2,5` exact op.
   4. Los `f(x) = 4` exact op.
   5. Waarom kun je `f(x) = 5` niet oplossen?


7. Los op `[-2pi,2pi]` exact op: `2 * sin(x) <= -sqrt(3)`.
   


8. Los exact op: `sin(2x) = sin(1/12 pi)`.
   

Verwerken

9. Bekijk de grafiek van `f(x) = sin(x)`.
   Los de volgende vergelijkingen op. Geef waar mogelijk exacte oplossingen en anders benaderingen in drie decimalen nauwkeurig.
   1. `sin(x) = 0,35`
   2. `sin(x) = -0,35`
   3. `sin(x) = 1/2sqrt(3)`
   4. `sin(x) = -1/2sqrt(2)`


10. Geef alle oplossingen van:
    1. `sin(x) = 1`
    2. `sin(x) = sin(1)`
    3. `sin(1) = x`


11. Gegeven is de functie `f` met `f(x) = 2 sin(x) - 1` op `[0,4pi]`.
    1. Bereken alle nulpunten van de grafiek van deze functie.
    2. Los op: `f(x) >= 0`.


12. Gegeven is de functie `g` met `g(x) = sin(2x)` op `[0,4pi]`.
    1. Los op: `g(x) = 0,5`
    2. Los op: `g(x) >= 0,5`.

Testen

13. Bekijk de grafiek van `f(x) = sin(x)`.
    Los de volgende vergelijkingen op. Geef waar mogelijk exacte oplossingen en anders benaderingen in drie decimalen nauwkeurig.
    1. `sin(x) = 0,95`
    2. `sin(x) = -0,95`
    3. `sin(x) = -1/2`


14. gegeven is de functie `f(x) = 4 sin(x) + 1` op `[-2pi,2pi]`.
    1. Bereken alle nulpunten van de grafiek van `f` in twee decimalen nauwkeurig.
    2. Los op `f(x) < 0`.


15. Los exact op: `sin(3x) = 0,5`.