
Radialen
Inleiding
Een regelmatige cirkelbeweging is een belangrijk periodiek verschijnsel.
De hoogte van een punt op een draaiende cirkel, uitgezet tegen de tijd,
levert een heel regelmatige periodieke grafiek: de sinusoïde.
Daarbij komt vanzelf een nieuwe manier te voorschijn om de grootte van een hoek aan te geven:
in radialen in plaats van in graden.
Je leert nu:
- de grafiek van y = sin(x) tekenen met x in radialen;
- graden omrekenen in radialen en omgekeerd.
Je kunt al:
- grafieken tekenen met de grafische rekenmachine;
- werken met sinus in rechthoekige driehoeken.
Verkennen
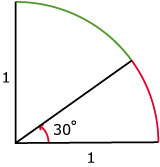 Hoeken druk je al heel lang in graden uit.
Toch hoeft dat niet, bekijk deze kwartcirkel maar eens.
Hij heeft een straal van 1.
Er staat een hoek van 30° in getekend.
Hoeken druk je al heel lang in graden uit.
Toch hoeft dat niet, bekijk deze kwartcirkel maar eens.
Hij heeft een straal van 1.
Er staat een hoek van 30° in getekend.
> Hoe lang is de getekende cirkelboog?
> Leg uit waarom 30° overeenkomt met een booglengte van .
> Als je de grootte van een hoek door zijn booglengte in een cirkel met straal 1 beschrijft,
krijg je hoeken in radialen. Dus 30° komt overeen met radialen.
Waarom is het van belang dat de cirkel waarin je de booglengte uitrekent een straal van 1 heeft?
> Reken maar eens een paar andere hoeken om van graden naar radialen.
Uitleg
Hier zie je een punt dat linksom (tegen de klok in) draait over een cirkel met straal 1, een
eenheidscirkel. Straal `OP` maakt een hoek `alpha` met de horizontale as. De hoogte `h` van punt is
rechthoekszijde in een rechthoekige driehoek. Deze hoogte is te berekenen met behulp van
goniometrie: `sin(alpha) = h/1 = h`. Dit is precies de `y`-co÷rdinaat van punt `P`: `y_P = sin(alpha)`.

De driehoek is alleen te gebruiken zolang `alpha < 90^o`. Maar het punt draait gewoon door, evenals
de hoek. Op deze manier wordt de sinus gedefinieerd voor hoeken van `90^o` en groter. Je ziet dat
voor sommige hoeken de sinus een negatief getal kan zijn!
Het punt kan ook rechtsom (met de klok mee) draaien, je krijgt dan negatieve hoeken. De sinus
van zoĺn negatieve hoek kan weer positief of negatief zijn.
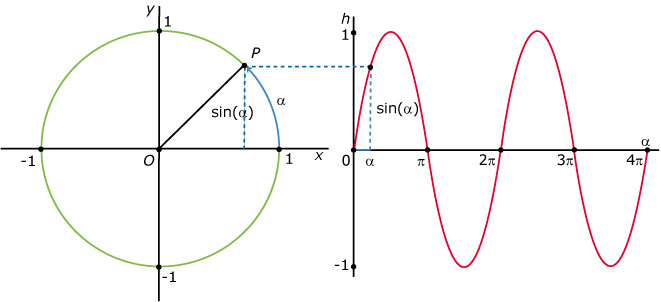
Hier zie je nog eens een eenheidscirkel. Maar nu staat op de horizontale as de afgelegde afstand
van `P` langs de eenheidscirkel, de booglengte van `alpha`. (Omdat de grafiek anders niet past is `alpha` op de horizontale as kleiner gemaakt dan de werkelijke booglengte. Er is een andere schaalverdeling op de as gebruikt dan op de cirkel.)
De omtrek van de cirkel is `2pi * text(straal) = 2pi * 1 = 2pi`. De periode van de sinusgrafiek is daarom niet
360, maar `2pi`.
Deze grafiek is de meest gebruikte sinusgrafiek. Je noemt dit de standaardsinuso´de.
Je werkt met `2pi` als met een gewoon getal, zonder nog aan hoeken te denken.
Het punt kan ook rechtsom (met de klok mee) draaien, er komen dan mintekens voor de
booglengtes.
‡
Opgaven
- Bekijk de Uitleg. Daarin zie je hoe je in een eenheidscirkel de lengte van de boog als maat
voor een hoek gebruikt. Je zegt dan dat de hoek `alpha` is uitgedrukt in radialen.
Teken een eenheidscirkel (een cirkel met een straal van 1 eenheid).
- Teken `P` als de draaihoek `alpha = 30^o`. Bereken de bijbehorende waarde van `h`. Hoeveel radialen is `alpha`?
- Teken `P` als de draaihoek `alpha = 150^o`. Bereken `h`. Hoeveel radialen is `alpha`?
- Teken `P` als de draaihoek `alpha = 210^o`. Bereken `h`. Hoeveel radialen is `alpha`?
- Teken `P` als de draaihoek `alpha = 270^o`. Bereken `h`. Hoeveel radialen is `alpha`?
- Hoeveel radialen hoort er bij `360^o`?
- Bij welke draaihoeken is `h = 1`? Geef je antwoord in graden en daarna in radialen.
-
Teken met je grafische rekenmachine de grafiek van `y = sin(x)`. Neem `x` in graden en stel het venster zo in dat `-360 <= x <= 720` en `-1,5 <= y <= 1,5`.
- Hoeveel periodes van de sinusgrafiek krijg je zo in beeld?
- Bereken `sin(30^o)` en `sin(390^o)`. Leg uit waarom beide uitkomsten gelijk zijn.
- Bereken `sin(30^o)` en `sin(150^o)`. Leg uit waarom beide uitkomsten gelijk zijn.
- Bij welke waarden van `x` vind je dezelfde uitkomst als `sin(30000^o)`?
- Bij welke waarden van `x` vind je dezelfde uitkomst als `sin(-10000^o)`?
-
Teken met je grafische rekenmachine de grafiek van `y = sin(x)`. Neem `x` in radialen en stel het venster zo in dat `-2pi <= x <= 6pi` en `-1,5 <= y <= 1,5`.
- Hoeveel periodes van de sinusgrafiek krijg je zo in beeld?
- Bereken `sin(1)` en `sin(1 + 2pi)`. Leg uit waarom beide uitkomsten gelijk zijn.
- Bereken `sin(1)` en `sin(pi - 1)`. Leg uit waarom beide uitkomsten gelijk zijn.
- Bij welke waarden van `x` vind je dezelfde uitkomst als `sin(211,5pi)`?
- Bij welke waarden van `x` vind je dezelfde uitkomst als `sin(-1500pi)`?
Theorie
Punt P beweegt over een eenheidscirkel (cirkel met straal 1). De bijbehorende draaihoek α is positief als je linksom draait, negatief als je rechtsom draait en kan alle waarden aannemen. De hoogte h van P t.o.v. het middelpunt van de cirkel is h = sin(α).
Voor een geschikte grafiek neem je liever α = x radialen.
De hoek wordt dan voorgesteld door de lengte van de bijbehorende boog op de eenheidscirkel.
360° komt overeen met 2π radialen.
Deze standaard sinusgrafiek is periodiek met periode 2π.

‡
Voorbeeld 1
Bij het omrekenen van graden naar radialen gebruik je: 360° wordt 2π radialen.
En dus:
- 1° wordt rad.
- 90° wordt rad.
En omgekeerd:
- 1 rad komt overeen met
-
rad komt overeen met
‡
Voorbeeld 2
Bepaal met je rekenmachine sin(10°), sin(100°), sin(1000°) en sin(10000°).
Waarom zijn de laatste twee uitkomsten hetzelfde?
Antwoord
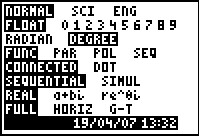 De draaihoek is gegeven in graden. Zorg er voor dat je rekenmachine met graden rekent.
De draaihoek is gegeven in graden. Zorg er voor dat je rekenmachine met graden rekent.
Ga na, dat sin(10°) ≈ 0,174; sin(100°) ≈ 0,985; sin(1000°) ≈ –0,985 en
sin(10000°) ≈ –0,985.
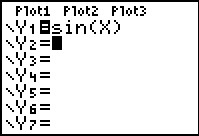
De grafiek van y = sin(x) met x in graden heeft een periode van 360°.
De laatste twee uitkomsten zijn gelijk omdat tussen 1000° en 10000° precies 9000 = 25 · 360° zit. Dat is precies 25 perioden.
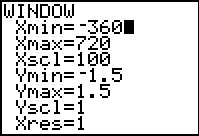
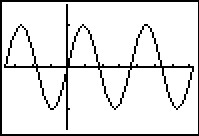
‡
Voorbeeld 3
Bepaal met je rekenmachine sin(1), sin(10), sin() en sin(360).
Antwoord
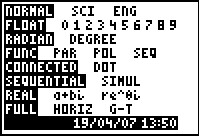 Er wordt nu in radialen gerekend, want er zijn geen gradentekens.
Laat je rekenmachine dan ook in radialen rekenen.
Er wordt nu in radialen gerekend, want er zijn geen gradentekens.
Laat je rekenmachine dan ook in radialen rekenen.
Ga na, dat sin(1) ≈ 0,841; sin(10) ≈ 0,544; sin() = 0,5 en sin(360) ≈ 0,959.
Hier zie je de grafiek van y = sin(x) met x in radialen.

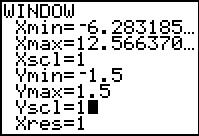
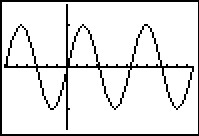
‡
Opgaven
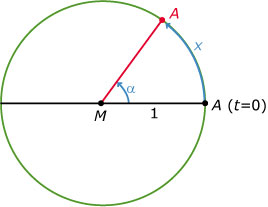 Punt `A` beweegt tegen de klok in over een eenheidscirkel met middelpunt `M`.
`alpha` is de draaihoek van `MA` in graden en `x` is de lengte van de cirkelboog die bij die draaihoek hoort.
Punt `A` beweegt tegen de klok in over een eenheidscirkel met middelpunt `M`.
`alpha` is de draaihoek van `MA` in graden en `x` is de lengte van de cirkelboog die bij die draaihoek hoort.
-
Hoeveel bedraagt `x` als `alpha = 360^o`?
-
Vul deze tabel in.
| `alpha` | `0^o` | `30^o` | `45^o` | `60^o` | `90^o` | `120^o` | `225^o` | `270^o` | `330^o` |
| `x` | | | | | | | | | |
`x` is de lengte van de eenheidscirkelboog in radialen.
Bekijk nu in Voorbeeld 1 hoe je systematisch van graden naar radialen omrekent en omgekeerd.
-
Hoeveel radialen is `10^o`?
-
Hoeveel graden is 10 radialen?
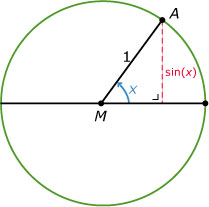 In Voorbeeld 2 bekijk je de waarden van `sin(x)` als `x` in graden is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
In Voorbeeld 2 bekijk je de waarden van `sin(x)` als `x` in graden is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
-
Hoeveel bedraagt de periode van deze sinusfunctie?
-
Leg uit waarom `sin(x) = sin(x + k * 360^o)`.
-
Leg uit waarom `sin(x) = sin(180^o - x)`.
-
Leg uit waarom `sin(-x) = -sin(x)`.
-
Waarom is `sin(45^o) = 1/2 sqrt(2)`? (Denk aan de stelling van Pythagoras.)
-
Voor welke twee hoeken `x` tussen `0^o` en `360^o` geldt: `sin(x) = - 1/2 sqrt(2)`?
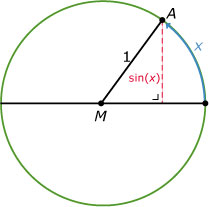 In Voorbeeld 3 bekijk je de waarden van `sin(x)` als `x` in radialen is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
In Voorbeeld 3 bekijk je de waarden van `sin(x)` als `x` in radialen is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
-
Hoeveel bedraagt de periode van deze sinusfunctie?
-
Leg uit waarom `sin(x) = sin(x + k * 2pi)`.
-
Leg uit waarom `sin(x) = sin(pi - x)`.
-
Welke waarden kan `sin(x)` aannemen?
-
Waarom is `sin(1/6 pi)` exact `0,5`? En waarom volgt daar uit dat `sin(1/3 pi) = 1/2 sqrt(3)`?
-
Geef de volgende waarden exact: `sin(5 1/6 pi), sin(-1 5/6 pi), sin(2 3/4 pi)`.
-
Gegeven is `sin(x) = 0,1` met `x` in radialen.
- Geef alle mogelijke hoeken `x` die hieraan voldoen en waarvoor geldt `0 <= x < 2pi` aan in een eenheidscirkel.
- Hoe groot is `sin(x + 2pi)`?
- Hoe groot is `sin(x + pi)`?
- Hoe groot is `sin(pi - x)`?
- Hoe groot is `sin(15pi + x)`?
- Hoe groot is `sin(16pi + x)`?
-
Voor welke exacte waarden van `x` (in radialen) geldt `sin(x) = 0,5`?
Verwerken
Vanaf nu is (tenzij anders vermeld) bij `sin(x)` de variabele `x` altijd in radialen uitgedrukt.
-
Deze hoeken zijn gegeven in graden. Bereken de bijbehorende booglengtes in de eenheidscirkel in radialen.
- `30^0, 20^0, 10^0, 270^0, 360^0, 455^0, 780^0`.
Hier zijn booglengtes in de eenheidscirkel gegeven. Bereken de bijbehorende hoeken in graden nauwkeurig.
- `1/2 pi; 1/3 pi; 3/4 pi; 1; pi; 3,1416; 10pi`.
-
Bekijk de grafiek van `f(x) = sin(x)` op `[-2pi,4pi]`.
-
Bereken `f(5 * 1/6pi)` en `5 * f(1/6 pi)` exact. Verklaar het verschil.
-
Bereken `f(1/4pi)` en `f(-1/4pi)` exact. Verklaar de overeenkomst.
-
Laat in deze grafiek zien dat `sin(-x) = -sin(x)`.
-
Laat met behulp van deze grafiek zien dat `sin(x) = sin(3pi - x)`.
-
Met een grafiek kun je natuurlijk niets bewijzen. Met behulp van een figuur in de eenheidscirkel wel. Bewijs nu de twee voorgaande eigenschappen.
-
Gegeven `sin(x) = 0,6`.
- Geef in een eenheidscirkel alle waarden van `x` met `0 <= x < 2pi` aan die hieraan voldoen.
- Schrijf alle waarden van `x` op die hier aan voldoen. Benaderingen in drie decimalen nauwkeurig.
-
Gegeven `sin(x) = -0,5`.
- Geef in een eenheidscirkel alle waarden van `x` met `0 <= x < 2pi` aan die hieraan voldoen.
- Schrijf alle waarden van `x` op die hier aan voldoen. Geef exacte waarden.
Testen
-
Geef de antwoorden exact indien mogelijk, anders in drie decimalen benaderd.
- Deze hoeken zijn gegeven in graden. Reken om naar radialen.
`60^o, 45^o, 180^o, 300^o, 330^o, 350^o, -350^o`.
- Deze booglengtes van een eenheidscirkel zijn gegeven in radialen. Bereken de bijbehorende hoeken in graden.
`pi, 1/3pi, -1/4pi, 2pi, 5/6pi, 13/12pi, 2, 5/3pi`.
-
Bekijk de grafiek van `f(x) = sin(x)` op `[-2pi,4pi]`.
-
Bereken `f(1/4pi + 1/3pi)` en `f(1/4pi) + f(1/3pi)`. Verklaar het verschil.
-
Bereken `f(1/4pi)` en `f(-3/4pi)` exact. Verklaar de overeenkomst.
-
Laat in deze grafiek zien dat `sin(-x) = sin(pi + x)`.
-
Bewijs deze eigenschap met behulp van een eenheidscirkel.
-
Gegeven `sin(x) = -0,25`.
- Geef in een eenheidscirkel alle waarden van `x` met `0 <= x < 2pi` aan die hieraan voldoen.
- Schrijf alle waarden van `x` op die hier aan voldoen. Benaderingen in drie decimalen nauwkeurig.
 Hoeken druk je al heel lang in graden uit.
Toch hoeft dat niet, bekijk deze kwartcirkel maar eens.
Hij heeft een straal van 1.
Er staat een hoek van 30° in getekend.
Hoeken druk je al heel lang in graden uit.
Toch hoeft dat niet, bekijk deze kwartcirkel maar eens.
Hij heeft een straal van 1.
Er staat een hoek van 30° in getekend.

 Hoeken druk je al heel lang in graden uit.
Toch hoeft dat niet, bekijk deze kwartcirkel maar eens.
Hij heeft een straal van 1.
Er staat een hoek van 30° in getekend.
Hoeken druk je al heel lang in graden uit.
Toch hoeft dat niet, bekijk deze kwartcirkel maar eens.
Hij heeft een straal van 1.
Er staat een hoek van 30° in getekend.











 Punt `A` beweegt tegen de klok in over een eenheidscirkel met middelpunt `M`.
`alpha` is de draaihoek van `MA` in graden en `x` is de lengte van de cirkelboog die bij die draaihoek hoort.
Punt `A` beweegt tegen de klok in over een eenheidscirkel met middelpunt `M`.
`alpha` is de draaihoek van `MA` in graden en `x` is de lengte van de cirkelboog die bij die draaihoek hoort.
 In Voorbeeld 2 bekijk je de waarden van `sin(x)` als `x` in graden is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
In Voorbeeld 2 bekijk je de waarden van `sin(x)` als `x` in graden is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
 In Voorbeeld 3 bekijk je de waarden van `sin(x)` als `x` in radialen is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
In Voorbeeld 3 bekijk je de waarden van `sin(x)` als `x` in radialen is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.