
Radialen
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Uitleg
Bekijk in de Uitleg wat een eenheidscirkel is en hoe je met behulp daarvan kunt omrekenen van hoeken in graden naar booglengtes in radialen.
Opgaven
- Bekijk de Uitleg. Daarin zie je hoe je in een eenheidscirkel de lengte van de boog als maat
voor een hoek gebruikt. Je zegt dan dat de hoek `alpha` is uitgedrukt in radialen.
Teken een eenheidscirkel (een cirkel met een straal van 1 eenheid).
- Teken `P` als de draaihoek `alpha = 30^o`. Bereken de bijbehorende waarde van `h`. Hoeveel radialen is `alpha`?
- Teken `P` als de draaihoek `alpha = 150^o`. Bereken `h`. Hoeveel radialen is `alpha`?
- Teken `P` als de draaihoek `alpha = 210^o`. Bereken `h`. Hoeveel radialen is `alpha`?
- Teken `P` als de draaihoek `alpha = 270^o`. Bereken `h`. Hoeveel radialen is `alpha`?
- Hoeveel radialen hoort er bij `360^o`?
- Bij welke draaihoeken is `h = 1`? Geef je antwoord in graden en daarna in radialen.
-
Teken met je grafische rekenmachine de grafiek van `y = sin(x)`. Neem `x` in graden en stel het venster zo in dat `-360 <= x <= 720` en `-1,5 <= y <= 1,5`.
- Hoeveel periodes van de sinusgrafiek krijg je zo in beeld?
- Bereken `sin(30^o)` en `sin(390^o)`. Leg uit waarom beide uitkomsten gelijk zijn.
- Bereken `sin(30^o)` en `sin(150^o)`. Leg uit waarom beide uitkomsten gelijk zijn.
- Bij welke waarden van `x` vind je dezelfde uitkomst als `sin(30000^o)`?
- Bij welke waarden van `x` vind je dezelfde uitkomst als `sin(-10000^o)`?
-
Teken met je grafische rekenmachine de grafiek van `y = sin(x)`. Neem `x` in radialen en stel het venster zo in dat `-2pi <= x <= 6pi` en `-1,5 <= y <= 1,5`.
- Hoeveel periodes van de sinusgrafiek krijg je zo in beeld?
- Bereken `sin(1)` en `sin(1 + 2pi)`. Leg uit waarom beide uitkomsten gelijk zijn.
- Bereken `sin(1)` en `sin(pi - 1)`. Leg uit waarom beide uitkomsten gelijk zijn.
- Bij welke waarden van `x` vind je dezelfde uitkomst als `sin(211,5pi)`?
- Bij welke waarden van `x` vind je dezelfde uitkomst als `sin(-1500pi)`?
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
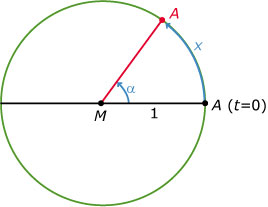 Punt `A` beweegt tegen de klok in over een eenheidscirkel met middelpunt `M`.
`alpha` is de draaihoek van `MA` in graden en `x` is de lengte van de cirkelboog die bij die draaihoek hoort.
Punt `A` beweegt tegen de klok in over een eenheidscirkel met middelpunt `M`.
`alpha` is de draaihoek van `MA` in graden en `x` is de lengte van de cirkelboog die bij die draaihoek hoort.
-
Hoeveel bedraagt `x` als `alpha = 360^o`?
-
Vul deze tabel in.
| `alpha` | `0^o` | `30^o` | `45^o` | `60^o` | `90^o` | `120^o` | `225^o` | `270^o` | `330^o` |
| `x` | | | | | | | | | |
`x` is de lengte van de eenheidscirkelboog in radialen.
Bekijk nu in Voorbeeld 1 hoe je systematisch van graden naar radialen omrekent en omgekeerd.
-
Hoeveel radialen is `10^o`?
-
Hoeveel graden is 10 radialen?
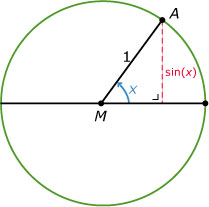 In Voorbeeld 2 bekijk je de waarden van `sin(x)` als `x` in graden is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
In Voorbeeld 2 bekijk je de waarden van `sin(x)` als `x` in graden is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
-
Hoeveel bedraagt de periode van deze sinusfunctie?
-
Leg uit waarom `sin(x) = sin(x + k * 360^o)`.
-
Leg uit waarom `sin(x) = sin(180^o - x)`.
-
Leg uit waarom `sin(-x) = -sin(x)`.
-
Waarom is `sin(45^o) = 1/2 sqrt(2)`? (Denk aan de stelling van Pythagoras.)
-
Voor welke twee hoeken `x` tussen `0^o` en `360^o` geldt: `sin(x) = - 1/2 sqrt(2)`?
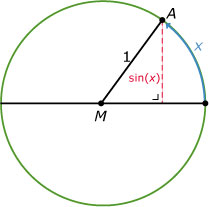 In Voorbeeld 3 bekijk je de waarden van `sin(x)` als `x` in radialen is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
In Voorbeeld 3 bekijk je de waarden van `sin(x)` als `x` in radialen is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
-
Hoeveel bedraagt de periode van deze sinusfunctie?
-
Leg uit waarom `sin(x) = sin(x + k * 2pi)`.
-
Leg uit waarom `sin(x) = sin(pi - x)`.
-
Welke waarden kan `sin(x)` aannemen?
-
Waarom is `sin(1/6 pi)` exact `0,5`? En waarom volgt daar uit dat `sin(1/3 pi) = 1/2 sqrt(3)`?
-
Geef de volgende waarden exact: `sin(5 1/6 pi), sin(-1 5/6 pi), sin(2 3/4 pi)`.
-
Gegeven is `sin(x) = 0,1` met `x` in radialen.
- Geef alle mogelijke hoeken `x` die hieraan voldoen en waarvoor geldt `0 <= x < 2pi` aan in een eenheidscirkel.
- Hoe groot is `sin(x + 2pi)`?
- Hoe groot is `sin(x + pi)`?
- Hoe groot is `sin(pi - x)`?
- Hoe groot is `sin(15pi + x)`?
- Hoe groot is `sin(16pi + x)`?
-
Voor welke exacte waarden van `x` (in radialen) geldt `sin(x) = 0,5`?
Verwerken
Vanaf nu is (tenzij anders vermeld) bij `sin(x)` de variabele `x` altijd in radialen uitgedrukt.
-
Deze hoeken zijn gegeven in graden. Bereken de bijbehorende booglengtes in de eenheidscirkel in radialen.
- `30^0, 20^0, 10^0, 270^0, 360^0, 455^0, 780^0`.
Hier zijn booglengtes in de eenheidscirkel gegeven. Bereken de bijbehorende hoeken in graden nauwkeurig.
- `1/2 pi; 1/3 pi; 3/4 pi; 1; pi; 3,1416; 10pi`.
-
Bekijk de grafiek van `f(x) = sin(x)` op `[-2pi,4pi]`.
-
Bereken `f(5 * 1/6pi)` en `5 * f(1/6 pi)` exact. Verklaar het verschil.
-
Bereken `f(1/4pi)` en `f(-1/4pi)` exact. Verklaar de overeenkomst.
-
Laat in deze grafiek zien dat `sin(-x) = -sin(x)`.
-
Laat met behulp van deze grafiek zien dat `sin(x) = sin(3pi - x)`.
-
Met een grafiek kun je natuurlijk niets bewijzen. Met behulp van een figuur in de eenheidscirkel wel. Bewijs nu de twee voorgaande eigenschappen.
-
Gegeven `sin(x) = 0,6`.
- Geef in een eenheidscirkel alle waarden van `x` met `0 <= x < 2pi` aan die hieraan voldoen.
- Schrijf alle waarden van `x` op die hier aan voldoen. Benaderingen in drie decimalen nauwkeurig.
-
Gegeven `sin(x) = -0,5`.
- Geef in een eenheidscirkel alle waarden van `x` met `0 <= x < 2pi` aan die hieraan voldoen.
- Schrijf alle waarden van `x` op die hier aan voldoen. Geef exacte waarden.
Testen
-
Geef de antwoorden exact indien mogelijk, anders in drie decimalen benaderd.
- Deze hoeken zijn gegeven in graden. Reken om naar radialen.
`60^o, 45^o, 180^o, 300^o, 330^o, 350^o, -350^o`.
- Deze booglengtes van een eenheidscirkel zijn gegeven in radialen. Bereken de bijbehorende hoeken in graden.
`pi, 1/3pi, -1/4pi, 2pi, 5/6pi, 13/12pi, 2, 5/3pi`.
-
Bekijk de grafiek van `f(x) = sin(x)` op `[-2pi,4pi]`.
-
Bereken `f(1/4pi + 1/3pi)` en `f(1/4pi) + f(1/3pi)`. Verklaar het verschil.
-
Bereken `f(1/4pi)` en `f(-3/4pi)` exact. Verklaar de overeenkomst.
-
Laat in deze grafiek zien dat `sin(-x) = sin(pi + x)`.
-
Bewijs deze eigenschap met behulp van een eenheidscirkel.
-
Gegeven `sin(x) = -0,25`.
- Geef in een eenheidscirkel alle waarden van `x` met `0 <= x < 2pi` aan die hieraan voldoen.
- Schrijf alle waarden van `x` op die hier aan voldoen. Benaderingen in drie decimalen nauwkeurig.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Radialen > Theorie Punt `A` beweegt tegen de klok in over een eenheidscirkel met middelpunt `M`.
`alpha` is de draaihoek van `MA` in graden en `x` is de lengte van de cirkelboog die bij die draaihoek hoort.
Punt `A` beweegt tegen de klok in over een eenheidscirkel met middelpunt `M`.
`alpha` is de draaihoek van `MA` in graden en `x` is de lengte van de cirkelboog die bij die draaihoek hoort.
 In Voorbeeld 2 bekijk je de waarden van `sin(x)` als `x` in graden is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
In Voorbeeld 2 bekijk je de waarden van `sin(x)` als `x` in graden is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
 In Voorbeeld 3 bekijk je de waarden van `sin(x)` als `x` in radialen is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.
In Voorbeeld 3 bekijk je de waarden van `sin(x)` als `x` in radialen is.
Hier zie je nog eens waar je de waarden van `sin(x)` in de eenheidscirkel vindt.