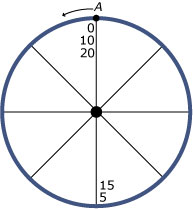
 Een wiel draait met steeds dezelfde snelheid rond en maakt één omwenteling in 10 seconden.
Op tijdstip t = 0 staat punt A precies bovenaan. Het punt gaat naar links.
Een wiel draait met steeds dezelfde snelheid rond en maakt één omwenteling in 10 seconden.
Op tijdstip t = 0 staat punt A precies bovenaan. Het punt gaat naar links.

Er zijn veel verschijnselen die zich herhalen in tijd of ruimte.
Bijvoorbeeld een muzieknummer dat je afspeelt met herhaling; een voetbalfragment dat telkens wordt herhaald; zomer en winter; de dagen van de week; een golvend landschap heuvel op heuvel af.
Je noemt dat: periodieke verschijnselen.
Als het verschijnsel ook nog met een functie te beschrijven is,
spreek je van een periodieke functie.
Als je één geschikt stukje kent (de periode) kun je het vervolg helemaal voorspellen.
In dit onderdeel zul je dat voor verschillende soorten van periodieke functies doen.
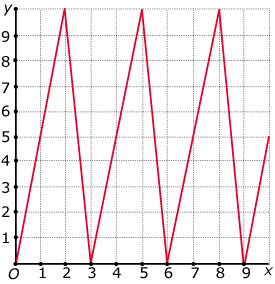
Een mier loopt op een verticaal vlak vierkantjes: 5 cm omhoog, 5 cm horizontaal, 5 cm recht naar beneden, 5 cm horizontaal, enz. De snelheid is constant 1 cm/s. Hier zie je de grafiek van de hoogte h boven de horizontale as afhankelijk van de tijd `t`.
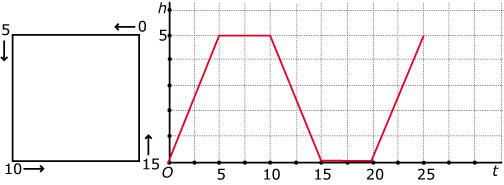
> Leg uit waarom de grafiek er zo uitziet.
> Welke periode heeft de grafiek?
> Hoe hoog zit de mier na 614 seconden?

Het is maandag. Welke dag is het over 100 dagen?
Bij de dagen van de week is sprake van herhaling per 7 dagen. Je zegt dat dit periodieke verschijnsel een periode heeft van 7 dagen.
Het is dus opnieuw maandag na bijvoorbeeld 70 dagen, na 77, 84, 91 en 98 dagen. Dus over 99 dagen is het dinsdag en over 100 dagen is het woensdag.
In dit soort situaties moet je één basispatroon kiezen dat zich telkens herhaalt. Dat kan zijn maandag tot en met zondag (dus 7 dagen), maar bijvoorbeeld ook zondag tot en met zaterdag (ook 7 dagen) of donderdag tot en met woensdag.
 Een wiel draait met steeds dezelfde snelheid rond en maakt één omwenteling in 10 seconden.
Op tijdstip t = 0 staat punt A precies bovenaan. Het punt gaat naar links.
Een wiel draait met steeds dezelfde snelheid rond en maakt één omwenteling in 10 seconden.
Op tijdstip t = 0 staat punt A precies bovenaan. Het punt gaat naar links.
Omdat het wiel in 10 seconden ronddraait is dat op t = 10, maar ook op t = 20, t = 30, t = 40, enz. En als het wiel al aan het draaien was, ook op t = –10, t = –20, t = –30, enz.
Het valt nog niet mee om dat wiskundig netjes op te schrijven.
Het kan zo: t = 0 + k · 10 met .
Hierin is
een schrijfwijze voor de verzameling van alle gehele getallen.
Dat duurt drie vierde van een omwenteling, dus 7,5 seconden.
Maar daar kan weer 10 bij of af, zo vaak als je maar wilt.
Dus t = ..., –12,5; –2,5; 7,5; 17,5; 27,5; ...
Anders gezegd: t = 2,5 + k · 10 met .
‡
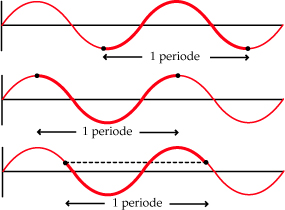
De periode van een periodiek verschijnsel is de lengte van het interval waarop de grafiek zich telkens herhaalt.
Je hebt nog wel keuze, welk stuk je daarvoor neemt.
Zo kun je bij een golf een stukje nemen van een maximum tot het eerstvolgend maximum.
Maar ook van een minimum tot het eerstvolgend minimum.
Of van een willekeurig punt tot het (PAS OP!) tweede volgende punt op dezelfde hoogte op de grafiek.
Voor de lengte van het interval waarop de grafiek zich herhaalt maakt het niets uit, welk stuk van de grafiek je neemt.
Die lengte is altijd gelijk als de grafiek zuiver periodiek is.
Bij de dagen van de week is de periode 7 dagen.
Bij een draaiend wiel is de periode bijvoorbeeld 10 seconden.
Soms wordt de periode ook wel de golflengte genoemd.
Het aantal periodes per (tijds)eenheid heet de frequentie.
‡
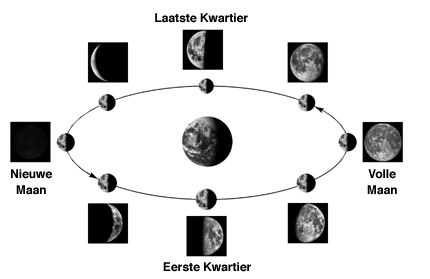
De schijngestalten van de maan: nieuwe maan, eerste kwartier (halve maan), volle maan, laatste kwartier (weer halve maan), nieuwe maan, enz., zijn een periodiek verschijnsel met een periode van gemiddeld ongeveer 30 dagen (in de loop van het jaar wisselt de lengte een beetje).
Op 14 januari 2006 was het volle maan.
Bereken op welke datum in mei 2006 het ook volle maan was.
Je telt 30 dagen op bij 14 januari, dat geeft 13 februari.
Zo kom je stap voor stap op 15 maart, 14 april en dan op 13 mei.
De volgende volle maan valt niet meer in mei.
Antwoord: 13 mei 2006.
Meer lezen over de schijngestalten van de maan?
Ga naar » urania.be
‡
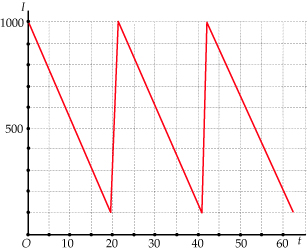
Een opslagtank bevat 1000 liter brandstof op dag t = 0. In 20 dagen neemt dat gelijkmatig af tot 100 liter. Dan wordt hij in 1 dag bijgevuld tot 1000 liter, enz.
Hoeveel zit erin na 75 dagen?
De inhoud is een periodieke functie met een periode van 21 dagen.
Na 75 dagen is de inhoud hetzelfde als hij was na 54, na 33 en na 12 dagen.
Je bekijkt daarom de lineaire functie door de punten (0,1000) en (20,100).
Hiervan is de helling = –45.
Dus is de gevraagde inhoud 1000 – 12 · 45 = 460 liter.
‡
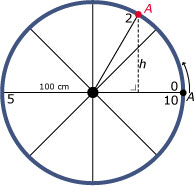
Je bekijkt een wiel dat in 10 seconden ronddraait.
Punt A is helemaal rechts op het tijdstip t = 0.
Gegeven is dat de straal MA van het wiel 100 centimeter is.
De hoogte h(t) van punt A meet je ten opzichte van de as van het wiel,
zodat op tijdstip t = 0 de hoogte ook 0 cm is.
Hoe hoog is het punt op tijdstip t = 42?
h(t) heeft een periode van 10. Dus is de hoogte op t = 42 hetzelfde als de hoogte op t = 2.
Punt A heeft dan van de cirkel doorlopen en is dus ·360° = 72° gedraaid.
Voor het berekenen van de hoogte heb je de sinus nodig:
en dus: h = 100 · sin(72°) ≈ 95,1 cm.
Dus is op t = 42 de hoogte ongeveer 95 cm.
‡
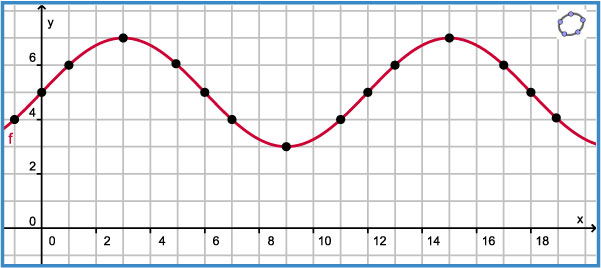
 Hier zie je een punt `P` op de tip van een rotorblad van een ronddraaiende windmolen. Hieronder is de grafiek van de functie `h(t)` getekend, waarin `h` de hoogte van punt `P` boven de grond in meter voorstelt en `t` de tijd in seconden is.
Hier zie je een punt `P` op de tip van een rotorblad van een ronddraaiende windmolen. Hieronder is de grafiek van de functie `h(t)` getekend, waarin `h` de hoogte van punt `P` boven de grond in meter voorstelt en `t` de tijd in seconden is.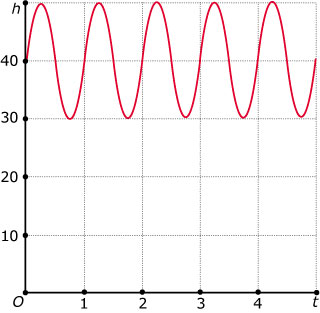
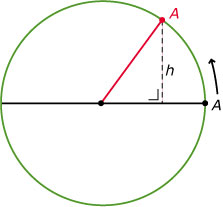 Punt `A` ligt op een wiel op afstand 1 van de as. De hoogte van punt `A` ten opzichte van de as noem je `h(t)`. Punt `A` begint rechts, dus `h(0) = 0`.
Het wiel draait in 6 seconden rond, linksom. Dus `h(1,5) = 1`, want na `1,5` seconden is punt `A` precies boven.
Punt `A` ligt op een wiel op afstand 1 van de as. De hoogte van punt `A` ten opzichte van de as noem je `h(t)`. Punt `A` begint rechts, dus `h(0) = 0`.
Het wiel draait in 6 seconden rond, linksom. Dus `h(1,5) = 1`, want na `1,5` seconden is punt `A` precies boven.
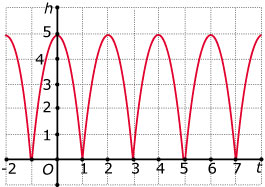 Een bal wordt omhooggeschoten op tijdstip `t = -1` en valt terug. Hij veert volkomen elastisch, waardoor hij alsmaar blijft stuiteren.
Gebruik de formule `h(t) = 5 - 5t^2` met `-1 <= t <= 1`.
`t` is in seconden, `h` is in meter.
Een bal wordt omhooggeschoten op tijdstip `t = -1` en valt terug. Hij veert volkomen elastisch, waardoor hij alsmaar blijft stuiteren.
Gebruik de formule `h(t) = 5 - 5t^2` met `-1 <= t <= 1`.
`t` is in seconden, `h` is in meter.