
Periodiciteit
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Uitleg
Lees in de Uitleg hoe je omgaat met herhaling bij bepaalde verschijnselen.
Opgaven
- Bestudeer eerst in de Uitleg hoe je een serie zich herhalende tijdstippen weergeeft.
- Op `t = 0` is het maandag. Leg uit waarom het `k * 7` dagen later weer maandag is. Waarom moet je aannemen dat `k` een geheel getal is?
- Welke dag is het `2 + k * 7` dagen later?
- Waarom heeft de vraag welke dag het `k * 5` dagen later is geen zin?
- Bekijk nu in de Uitleg nog eens het verhaal van het ronddraaiende wiel. Ga er van uit dat het punt `A` in 10 seconden rond draait en op `t = 0` bovenaan zit.
- Op welke tijdstippen zit punt `A` helemaal links?
- Geef in de figuur aan waar punt `A` zit op `t = 7 + k * 10` (teken eventueel zelf zo'n wiel, de grootte is onbelangrijk).
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
-
Bekijk in de Theorie wat een periodiek verschijnsel is en wat je verstaat onder de periode en de frequentie van zo'n verschijnsel.
Bekijk Voorbeeld 1 over de schijngestalten van de maan.
-
Welke periode heeft dit verschijnsel?
-
Met welke frequentie is het volle maan?
-
Op welke datum was het volle maan in januari 2007?
-
In Voorbeeld 2 gaat het over het leeglopen en weer vullen van een brandstoftank.
De hoogte van de brandstof in de tank is een periodiek verschijnsel.
-
Hoeveel bedraagt de periode?
-
Leg uit waarom er 550 liter in de tank zit op `t = 10 + k * 21 vv t = 20,5 + k * 21`.
-
Voor welke waarden van `t` zit er 100 liter in de tank?
-
Hoeveel zit er in de brandstoftank na 500 dagen?
-
Hier zie je de grafiek van de periodieke functie `f`. Het domein is `RR` (dus de grafiek loopt naar beide kanten oneindig ver door).
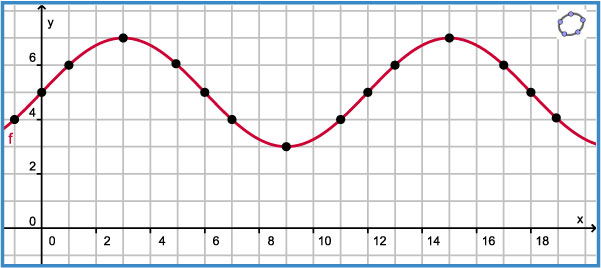
- Bepaal de periode van deze functie.
- Bepaal `f(81)` en `f(91)`.
- Los op: `f(x) = 6` met `75 <= x <= 85`.
- Bepaal `f(-5)`.
- Los op: `f(x) = 4` met `-100 <= x <= -90`.
-
Bestudeer Voorbeeld 3 over het ronddraaiende punt `A`.
- Bereken de hoogte `h` als `t = 1`.
- Hoe groot is `h` als `t = 31`?
- Bereken de hoogtes voor de gehele waarden van `t` vanaf 0 tot en met 10. Teken een grafiek van `h` als functie van `t`.
- Hoe ziet de grafiek er uit als de waarden van `t` vanaf 0 tot en met 100 lopen?
 Hier zie je een punt `P` op de tip van een rotorblad van een ronddraaiende windmolen. Hieronder is de grafiek van de functie `h(t)` getekend, waarin `h` de hoogte van punt `P` boven de grond in meter voorstelt en `t` de tijd in seconden is.
Hier zie je een punt `P` op de tip van een rotorblad van een ronddraaiende windmolen. Hieronder is de grafiek van de functie `h(t)` getekend, waarin `h` de hoogte van punt `P` boven de grond in meter voorstelt en `t` de tijd in seconden is.
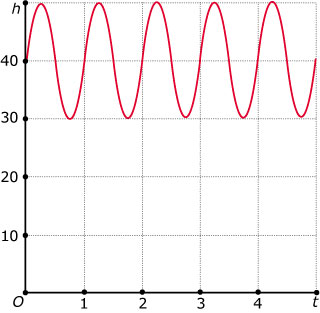
-
Met welke periode draait het rotorblad van de windmolen? Met welke frequentie (omwentelingen per minuut) draait het rotorblad?
-
Hoe hoog zit de as van de windmolen boven de grond? En hoe lang is het rotorblad?
-
De wind neemt toe, de windmolen gaat twee keer zo snel draaien. Teken de bijbehorende grafiek.
-
Teken ook de grafiek van de hoogte van de tip van één van de twee andere rotorbladen.
-
Een punt `P` beweegt linksom over een cirkel met straal 1 om de oorsprong `O` van een `Oxy`-assenstelsel. De afstand `a` die het punt heeft afgelegd hangt af van de hoek `alpha` waarover `OP` is gedraaid.
Neem aan dat `a = 0` als `alpha = 0`.
-
Hoeveel is `a(90^o)`? En `a(180^o)`? (Geef exacte waarden.)
-
Leg uit waarom je nu te maken krijgt met hoeken die groter zijn dan `180^o`. Leg ook uit waarom de draaihoek zelfs groter kan zijn dan `360^o`.
-
Wat zou een draaihoek van `-60^o` betekenen?
-
Bepaal nu `a(360^o)`, `a(450^o)`, `a(60^o)` en `a(-30^o)`.
-
Hoeveel is `a(1^o)`?
-
Is `a(alpha)` een periodieke functie? Licht je antwoord toe.
Verwerken
-
Bekijk deze grafiek van de periodieke functie `f`.
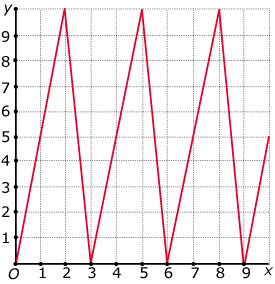
- Bereken `f(25)`.
- Voor welke waarden van `x` is `f(x) = 10`?
- Los op: `f(x) = 5` met `0 <= x <= 9`.
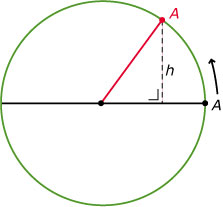 Punt `A` ligt op een wiel op afstand 1 van de as. De hoogte van punt `A` ten opzichte van de as noem je `h(t)`. Punt `A` begint rechts, dus `h(0) = 0`.
Het wiel draait in 6 seconden rond, linksom. Dus `h(1,5) = 1`, want na `1,5` seconden is punt `A` precies boven.
Punt `A` ligt op een wiel op afstand 1 van de as. De hoogte van punt `A` ten opzichte van de as noem je `h(t)`. Punt `A` begint rechts, dus `h(0) = 0`.
Het wiel draait in 6 seconden rond, linksom. Dus `h(1,5) = 1`, want na `1,5` seconden is punt `A` precies boven.
-
Bereken `h(4,5)`, `h(10,5)` en `h(16,5)`.
-
Bereken `h(0,75)` exact.
-
Bereken exact `h(6,75)`, `h(12,75)` en `h(-5,25)`.
-
Los op: `h(t) = h(0,75)`.
-
Een torenklok heeft een grote wijzer met een lengte van `1,5` m. De beide wijzers zitten bevestigd op de as van de klok op 45 m boven de grond.
Punt `T` stelt de tip van deze grote wijzer voor. De hoogte `h` in m van `T` boven de grond hangt af van de draaihoek `alpha`. Neem aan dat `alpha = 0` om 12:00 uur.
- Hoe hoog zit `T` boven de grond op 2:10 uur?
- Schets een grafiek van `h(alpha)`.
- Er zijn twee tijdstippen waarop `h(alpha) = 46`. De bijbehorende punten waar `T` dan zit zijn `A` en `B`. Hoe ver zitten die punten `A` en `B` van elkaar?
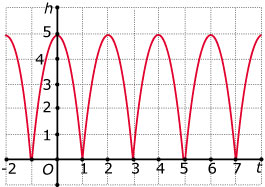 Een bal wordt omhooggeschoten op tijdstip `t = -1` en valt terug. Hij veert volkomen elastisch, waardoor hij alsmaar blijft stuiteren.
Gebruik de formule `h(t) = 5 - 5t^2` met `-1 <= t <= 1`. `t` is in seconden, `h` is in meter.
Een bal wordt omhooggeschoten op tijdstip `t = -1` en valt terug. Hij veert volkomen elastisch, waardoor hij alsmaar blijft stuiteren.
Gebruik de formule `h(t) = 5 - 5t^2` met `-1 <= t <= 1`. `t` is in seconden, `h` is in meter.
- Bereken `h(0)` en `h(0,5)`.
- Bepaal de periode van de grafiek.
- Bereken `h(6)` en `h(6,5)`.
- Bereken `h(15)` en `h(15,5)`.
- Hoe realistisch is dit rekenmodel?
Testen
-
Een grafiek bestaat in een `Oxy`-assenstelsel uit rechte lijnstukjes tussen de punten `(100,1000), (110,600), (140,1000), (150,600), (180,1000)`, enz. Het patroon gaat naar links en rechts oneindig ver door.
- Welke periode heeft deze grafiek?
- Bereken de waarde van `y` bij `x = 250`.
- Teken de grafiek met `0 <= x <= 100`.
- Bereken de waarde van `y` bij `x = -250`.
- Hoeveel getallen `x` met `0 <= x <= 100` bestaan er bij `y = 900?`
-
Een wiel met een straal van 30 cm draait linksom rond met constante snelheid. De omlooptijd is
20 seconden. De hoogte in centimeter van punt `A` aan de buitenkant van het wiel, gemeten ten
opzichte van het middelpunt, noem je `h(t)` met `t` in seconden. Het punt `A` begint bovenaan, dus `h(0) = 30`.
-
Met welke frequentie draait punt `A`?
-
Bereken `h(35)`.
-
Bereken `h(18)` in één decimaal nauwkeurig.
-
Bereken `h(76)` in één decimaal nauwkeurig.
-
Geef alle tijdstippen `t` met `-40 <= t <= 40` waarvoor geldt `h = 0`.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Periodiciteit > Theorie
 Hier zie je een punt `P` op de tip van een rotorblad van een ronddraaiende windmolen. Hieronder is de grafiek van de functie `h(t)` getekend, waarin `h` de hoogte van punt `P` boven de grond in meter voorstelt en `t` de tijd in seconden is.
Hier zie je een punt `P` op de tip van een rotorblad van een ronddraaiende windmolen. Hieronder is de grafiek van de functie `h(t)` getekend, waarin `h` de hoogte van punt `P` boven de grond in meter voorstelt en `t` de tijd in seconden is.

 Punt `A` ligt op een wiel op afstand 1 van de as. De hoogte van punt `A` ten opzichte van de as noem je `h(t)`. Punt `A` begint rechts, dus `h(0) = 0`.
Het wiel draait in 6 seconden rond, linksom. Dus `h(1,5) = 1`, want na `1,5` seconden is punt `A` precies boven.
Punt `A` ligt op een wiel op afstand 1 van de as. De hoogte van punt `A` ten opzichte van de as noem je `h(t)`. Punt `A` begint rechts, dus `h(0) = 0`.
Het wiel draait in 6 seconden rond, linksom. Dus `h(1,5) = 1`, want na `1,5` seconden is punt `A` precies boven.
 Een bal wordt omhooggeschoten op tijdstip `t = -1` en valt terug. Hij veert volkomen elastisch, waardoor hij alsmaar blijft stuiteren.
Gebruik de formule `h(t) = 5 - 5t^2` met `-1 <= t <= 1`. `t` is in seconden, `h` is in meter.
Een bal wordt omhooggeschoten op tijdstip `t = -1` en valt terug. Hij veert volkomen elastisch, waardoor hij alsmaar blijft stuiteren.
Gebruik de formule `h(t) = 5 - 5t^2` met `-1 <= t <= 1`. `t` is in seconden, `h` is in meter.