Periodiciteit

Antwoorden bij de opgaven

1. 1. Omdat je anders ook andere dagen in de week kunt uitkomen, bij `k = 1/7` bijvoorbeeld kom je op dinsdag.
   2. Woensdag.
   3. Omdat je dan steeds op wisselende dagen uitkomt.
2. 1. `t = 2,5 + k * 10`
   2. Daarbij hoort een hoek van `7/10 * 360^o = 252^o`.
3. 1. 30 dagen (ongeveer).
   2. `365/30` keer per jaar.
   3. 9 januari 2007.
4. 1. 21 dagen.
   2. Halverwege het leeglopen en halverwege het vollopen omdat beide lineair verlopen volgens de grafiek.
   3. `t = 20 + k * 21` dagen.
   4. Evenveel als na 17 dagen, dus `1000 - 17 * 45 = 235` liter.
5. 1. 12
   2. `f(81) = f(9) = 3` en `f(91) = f(7) = 4`.
   3. `x = 77 vv x = 85`.
   4. `f(-5) = 4`.
   5. `x = -97`.
6. 1. `h(1) = 100 * sin(36^o) ~~ 58,8` cm.
   2. `h(31) = h(1) ~~ 58,8` cm.
   3. 
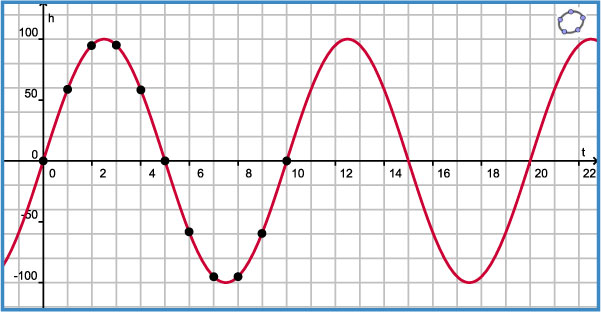
   4. Je krijgt dan 10 periodes in beeld.
7. 1. De periode is 1 sec, de frequentie is 60 omwentelingen per minuut.
   2. De as zit 40 m boven de grond, een roterblad is 10 m lang.
   3. De periode wordt nu `1/2` sec, de rest blijft gelijk.
   4. De grafiek begint nu op `t = 1/3` of `t = 2/3`.
8. 1. `a(90^o) = 1/2pi` en `a(180^o) = pi`.
   2. Je kunt punt `P` door blijven bewegen over de cirkel en toch de hoek steeds rekenen vanaf `t = 0`.
   3. Dat is `60^o` maar dan rechtsom gedraaid.
   4. `a(360^o) = 2pi`, `a(450^o) = a(90^o) = 1/2pi`, `a(60^o) = 1/3 pi` en `a(-30^o) = -1/6 pi`.
   5. `a(1^o) = 1/180 pi`.
   6. Nee, de uitkomsten worden steeds groter, het is een lineaire functie.
9. 1. `f(25) = f(1) = 5`.
   2. `x = 2 + k * 3`.
   3. `x = 1 vv x = 4 vv x = 7 vv x = 2,5 vv x = 5,5 vv x = 8,5`.
10. 1. `h(4,5) = -1`, `h(10,5) = -1` en `h(16,5) = -1`.
    2. `h(0,75) = 1/2 sqrt(2)` want je krijgt dan een rechthoekige driehoek met een hoek van `45^o` en die is gelijkbenig met rechthoekszijden `sqrt(1/2) = 1/2 sqrt(2)`.
    3. Die zijn allemaal `1/2 sqrt(2)` want de tijden verschillen precies een hele periode met `t = 0,75`.
    4. `t = 0,75 + k * 6 vv t = 2,25 + k * 6`.
11. 1. `h = 45 + 1,5 * cos(60^o) = 45,75` m.
    2. Vloeiende grafiek door `h(0) = 46,5`, `h(60) = 45,75`, `h(90) = 45`, `h(120) = 44,25`, `h(180) = 43,5`, `h(240) = 44,25`, `h(270) = 45`, `h(300) = 45,75` en `h(360) = 46,5`, etc...
    3. `h = 45 + 1,5 cos(alpha) = 46` geeft `alpha ~~ 48,2^o`. De gevraagde afstand is dan `2 * sin(48,2^o) ~~ 1,49` m.
12. 1. `h(0) = 5` en `h(0,5) = 3,75`.
    2. De periode is 2 seconden.
    3. `h(6) = h(0) = 5` en `h(6,5) = h(0,5) = 3,75`.
    4. `h(15) = h(-1) = 0` en `h(15,5) = h(-0,5) = 3,75`.
13. 1. 40
    2. `y(250) = y(130) = 600 + 2/3 * 400 = 866 2/3`.
    3. `y(0) = y(120) = 733 1/3`, `y(10) = y(130) = 866 2/3`, `y(20) = y(140) = 1000`, `y(30) = 600`, `y(40) = 733 1/3`, etc.
    4. `y(-250) = y(110) = 600`.
    5. 5
14. 1. 3 keer per minuut.
    2. `h(35) = h(15) = 0`.
    3. `h(18) = 30 * cos(18/20 * 360^o) ~~ 24,3` cm.
    4. `h(76) = h(16) = 30 * cos(16/20 * 360^o) ~~ 9,3` cm.
    5. `-35, -25, -15, -5, 5, 15, 25, 35`.