
Totaalbeeld
Samenvatten
Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Machtsfuncties. Een eigen samenvatting maken is nuttig.
Begrippenlijst:
51: recht evenredig met een macht — machtsverbanden;
52: machtsfuncties, eigenschappen afhankelijk van exponent — machtsvergelijking;
53: kwadratische functie — dal- en bergparabool — top — symmetrieas — kwadratische vergelijking;
54: kwadraat afsplitsen — abc-formule;
55: gebroken functie — wortelfunctie.
Activiteitenlijst:
51: machtsverbanden herkennen — heen- en terugrekenen bij machtsverbanden;
52: de eigenschappen van machtsfuncties vinden — werken met transformaties van machtsfuncties;
53: kwadratische functies tekenen — kwadratische vergelijkingen oplossen door terugrekenen;
54: kwadratische functies schrijven als machtsfuncties door kwadraat afsplitsen — de abc-formule gebruiken bij het oplossen van kwadratische vergelijkingen;
55: werken met gebroken functies en wortelfuncties die als machtsfuncties zijn te schrijven.
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Totaalbeeld > Achtergronden
Testen
-
Gegeven is de functie `f(x) = 10 - 2(x - 1)^5`.
-
Laat zien door welke transformaties de grafiek van `f` kan ontstaan uit die van `y = x^5`.
-
Bereken algebraïsch de snijpunten van de grafiek van `f` met de beide coördinaatassen.
-
Los algebraïsch op: `f(x) = 496`.
-
Los algebraïsch op: `f(x) > 8`.
-
Los de volgende vergelijkingen en ongelijkheden algebraïsch op:
-
`-0,5(x - 2)^4 + 45 <= 4,5`
-
`x(x - 2) = 3x - 6`
-
`x^3 - 4x^2 = 10x`
-
`6 - 0,1(x - 3)^(1/3) = 5`
-
`1/4 x^2 >= x + 5`
-
`4/((x - 2)^3) - 6 = 14`
-
Gegeven is voor elke waarde van `p` de functie `f(x) = 8 + 4px - px^2`.
-
Neem `p=1` en bereken de karakteristieken van de grafiek van `f`.
-
Voor welke waarden van `p` heeft de grafiek van `f` geen snijpunten met de `x`-as?
-
Voor welke waarden van `p` ligt de top van de grafiek van `f` op de lijn `y = 50 - 2x`?
-
Een kalkoen braden is lastig, omdat het enige tijd duurt voordat ook het binnenste
van de kalkoen op temperatuur komt. Hoe lang dat duurt hangt af van het gewicht.
Het is de kunst om de kalkoen zo lang te braden dat het binnenste net gaar
is. Je kunt dat niet controleren zonder de kalkoen aan te snijden. De optimale
braadtijd is daarom moeilijk vast te stellen. Gelukkig geven kookboeken vaak
aanwijzingen voor de braadtijd, die afhankelijk is van het gewicht van de kalkoen.
Onderzoekers hebben vastgesteld dat met de volgende formule het beste resultaat
wordt verkregen:
`t = 11g^(2/3)`
Hierin is `g` het gewicht van de kalkoen in kilogram en `t` de tijd in minuten die
nodig is om het binnenste van de kalkoen op een temperatuur van `85`°C te brengen.
-
Bereken hoe lang het bij een kalkoen van `3` kg duurt voor het binnenste op een temperatuur van `85`°C is.
Verwacht je dat een kalkoen van `6` kg daarvoor twee keer zoveel tijd nodig heeft?
-
Als het binnenste van de kalkoen een temperatuur heeft van `85`°C duurt het nog een tijd voordat de kalkoen gaar is.
Ga ervan uit dat die tijd `80` minuten is en dat die tijd afhangt van het gewicht van de kalkoen.
Geef de formule voor de totale braadtijd `T` van een kalkoen afhankelijk van het gewicht.
Is de totale braadtijd recht evenredig met een macht van het gewicht?
-
Verklaar waarom het minder moeilijk is om kooktijden vast te stellen dan braadtijden.
Is de kooktijd van bijvoorbeeld aardappels ook afhankelijk van het gewicht?
En de totale tijd dat aardappels op het fornuis moeten staan?
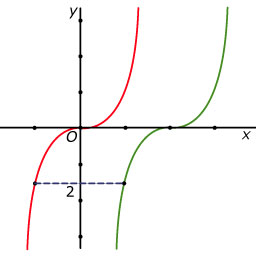 In de figuur zie je grafiek van `y_1 = x^3` en de grafiek van `y_2`. De grafiek
van `y_2` ligt rechts van die van `y_1` zo, dat alle verbindingslijnstukken
evenwijdig aan de `x`-as de lengte `2` hebben.
In de figuur zie je grafiek van `y_1 = x^3` en de grafiek van `y_2`. De grafiek
van `y_2` ligt rechts van die van `y_1` zo, dat alle verbindingslijnstukken
evenwijdig aan de `x`-as de lengte `2` hebben.
-
Geef het functievoorschrift van `y_2`.
-
De functie `v(x)` stelt de lengte van de verbindingslijnstukken die evenwijdig lopen aan de `y`-as voor.
Toon aan dat `v(x) = 6x^2 - 12x + 8`.
-
Voor welke waarden van `x` is de lengte van het verbindingslijnstuk evenwijdig aan de `y`-as minder dan `8`?
-
Bepaal de lengte van het kortste verbindingslijnstuk evenwijdig aan de `y`-as.
Toepassen
Kijkafstand
De formule voor de kijkafstand uit het begin van het onderwerp "Machtsfuncties" kun je heel goed zelf afleiden. Lees hierover in
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Totaalbeeld > Toepassingen
-
Voer deze afleiding zelf uit.
-
Verklaar waarom er verschil is tussen de formule uit het begin van het onderwerp "Machtsfuncties" en de formule die je zojuist hebt afgeleid.
-
Je kunt zo ook een formule afleiden voor de kijkafstand op de maan.
Zoek de daarvoor benodigde gegevens op.
-
Kun je op de maan verder of minder ver kijken dan op Aarde?
Examenopgaven
Diersoorten
Het lijkt aannemelijk dat er een verband bestaat tussen de oppervlakte van een gebied en het aantal verschillende diersoorten dat in dat gebied voorkomt. Een theorie hierover stelt dat het aantal verschillende diersoorten op een eiland in een
bepaalde klimaatzone alleen afhankelijk is van de oppervlakte van het eiland.
In deze opgave kijken we naar de verschillende soorten reptielen op eilanden in
het Caraïbisch gebied.
Onderzoekers telden op vele eilanden het aantal verschillende soorten
reptielen (`S`). In de volgende figuur zijn de gegevens van enkele
eilanden weergegeven.
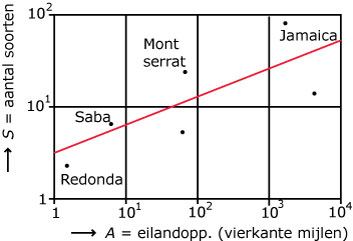
Volgens de theorie is het verband tussen de oppervlakte `A` ven een
eiland (in vierkante mijlen) en het aantal soorten reptielen (`S`) op dat
eilandente beschrijven met de formule `S = 3 * A^(0,30)`.
De lijn in de bovenstaande figuur is de grafiek die bij deze formule behoort.
-
Op het eiland Jamaica zijn meer soorten reptielen aangetroffen dan op grond van de theorie (de formule) verwacht mag worden.
Hoeveel soorten reptielen zou een even groot eiland volgens de theorie hebben? Licht je antwoord toe.
-
Binnen de theorie geldt als ruwe regel: "Bij een 10 keer zo groot eiland vinden we 2 keer zoveel diersoorten."
Laat zien dat dit uit de formule volgt.
Op een groot eiland worden veel verschillende soorten reptielen met
uitsterven bedreigd. Men wil maatregelen nemen om de natuur te beschermen.
Daarbij moet er een keuze worden gemaakt uit twee mogelijkheden:
- Oprichting van 1 groot natuurreservaat met een oppervlakte van 400 vierkante mijlen.
- Oprichting van 2 kleinere reservaten, elk met een oppervlakte van 200 vierkante mijlen.
Dergelijke natuurreservaten liggen geïsoleerd in de bewoonde wereld en kunnen
als 'eilanden' beschouwd worden.
Voor het schatten van het aantal soorten reptielen dat in zo’n reservaat zal voorkomen
kan de formule `S = 3* A^(0,30)` gebruikt worden.
Of voor 1 of 2 gekozen wordt, is mede afhankelijk van het aantal soorten dat de
twee kleinere reservaten gemeen zullen hebben. Men neemt aan dat er 8 soorten
reptielen zijn die zowel in het éne als het andere kleine reservaat zullen voorkomen.
Men wil de mogelijkheden kiezen waarbij in totaal zoveel mogelijk verschillende soorten reptielen zullen voorkomen.
-
Welke van de twee mogelijkheden zal men kiezen? Licht je antwoord toe.
(bron: examen wiskunde A havo 1993, eerste tijdvak)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Totaalbeeld > Achtergronden  In de figuur zie je grafiek van `y_1 = x^3` en de grafiek van `y_2`. De grafiek
van `y_2` ligt rechts van die van `y_1` zo, dat alle verbindingslijnstukken
evenwijdig aan de `x`-as de lengte `2` hebben.
In de figuur zie je grafiek van `y_1 = x^3` en de grafiek van `y_2`. De grafiek
van `y_2` ligt rechts van die van `y_1` zo, dat alle verbindingslijnstukken
evenwijdig aan de `x`-as de lengte `2` hebben.
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Totaalbeeld > Toepassingen
