Meer machtsfuncties

Inleiding

Alle functies die door transformatie kunnen ontstaan uit `y = x^p` (waarin `p` elk willekeurig reëel getal kan zijn) zijn machtsfuncties.
Dat geldt ook voor een gebroken functie f met bijvoorbeeld als functievoorschrift `f(x) = 2/(x + 4) + 5`, want dit is te schrijven als `f(x) = 2(x + 4)^(-1) + 5`.
En het geldt voor een wortelfunctie g met bijvoorbeeld als functievoorschrift `g(x) = 2 sqrt(x + 4) + 5`, want dit kun je schrijven als `g(x) = 2(x + 4)^(0,5) + 5`.
Over dergelijke functies gaat het hier...

Je leert nu:

• werken met gebroken functies waarvan de grafiek een hyperbool is;
• werken met wortelfuncties waarvan de grafiek een halve parabool is.

Je kunt al:

• werken met machtsfuncties in het algemeen;
• transformaties toepassen op functies;
• vergelijkingen en ongelijkheden algebraïsch oplossen.

Bekijk de grafieken van de twee functies uit de Inleiding.

> Welke karakteristieken heeft de grafiek van `f`? Schrijf domein en bereik van `f` op. Waarom is het ook een machtsfunctie?
> Welke karakteristieken heeft de grafiek van `g`? Schrijf domein en bereik van `g` op. Waarom is het ook een machtsfunctie?

Uitleg

Alle functies van de vorm `f(x) = x^p` met `p` een willekeurig reëel getal en alle functies die daaruit door transformatie kunnen ontstaan heten machtsfuncties.

Dat geldt voor alle lineaire en kwadratische functies, maar ook voor veel gebroken functies en veel wortelfuncties:

• Gebroken functies:
  • `f(x) = 200/(x + 30) - 100` is te schrijven als machtsfunctie `f(x) = 200(x + 30)^(-1) - 100`.
  • `g(x) = 40 - 1/(x^2)` is te schrijven als machtsfunctie `g(x) = -x^(-2) + 40`.
• Wortelfuncties:
  • `h(x) = 200sqrt(x + 30) - 100` is te schrijven als machtsfunctie `h(x) = 200(x + 30)^(1/2) - 100`.
  • `k(x) = 40 - root[3](x)` is te schrijven als machtsfunctie `k(x) = -x^(1/3) + 40`.

Al deze functies kun je door transformatie afleiden uit de bijbehorende machtsfunctie. Ze hebben daarom dezelfde eigenschappen.

‡

Opgaven

1. In de Uitleg zie je dat sommige gebroken functies als machtsfunctie kunnen worden geschreven. Schrijf de volgende gebroken functies als machtsfunctie als dat kan.
   1. `f(x) = 4 - 1/x^2`
   2. `g(x) = 1/(4 + x^2)`
   3. `h(x) = 2/((x-3)^4) +10`
   4. `k(x) = (4-x)/x`


2. In de Uitleg zie je dat sommige wortelfuncties als machtsfunctie kunnen worden geschreven. Schrijf de volgende wortelfuncties als machtsfunctie als dat kan.
   1. `f(x) = 4sqrt(x) + 3`
   2. `g(x) = sqrt(4 + x^2)`
   3. `h(x) = -5sqrt(2x - 8) + 6`
   4. `k(x) = 4/(sqrt(x)) + 3`

Theorie

Een machtsfunctie is een functie van de vorm `f(x) = a(x + b)^p + c`, waarin ook `p` elke reële waarde kan aannemen. Zo'n functie ontstaat door transformatie van `y = x^p`. Voorbeelden zijn:

• `p = 0`: `f(x) = a + c` een constante functie.

• `p = 1`: `f(x) = ax + d` een lineaire functie.

• `p = 2`: `f(x) = a(x + b)^2 + c` een kwadratische functie.

• `p = 1/2`: `f(x) = a(x + b)^(1/2) + c = a sqrt(x + b) + c` een wortelfunctie.

• `p = -1`: `f(x) = a(x + b)^(-1) + c = a/(x + b) + c` een hyperbolische functie.

‡

Voorbeeld 1

Gegeven is de functie `f` met `f(x) = 200/(x + 30) - 100`.
Leg uit hoe de grafiek van `f` kan ontstaan uit die van `y = x^(-1)` en bereken de snijpunten met de assen en de asymptoten.

Antwoord

`f(x) = 200/(x + 30) - 100 = 200(x + 30)^(-1) - 100`.
Dit is een machtsfunctie die ontstaat door transformatie van `y = x^(-1)`:

• eerst met `-30` verschuiven in de `x`-richting;
• vervolgens vermenigvuldigen met `200` in de `y`-richting (dus t.o.v. de `x`-as);
• tenslotte met `-100` verschuiven in de `y`-richting.

Deze transformaties kun je ook toepassen op de instellingen van het venster van je rekenmachine.
Je ziet de grafiek van `y = x^(-1)` goed in beeld als het venster is ingesteld op
`[-4,4] xx [-3,5]`.
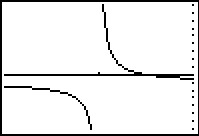Dit wordt na transformatie `[-34,-26] xx [-700,900]`.
Ga na, dat je dan de grafiek van f goed in beeld hebt. Je vindt verder:

• het snijpunt met de `y`-as:
  `f(0) = 200/30 - 100 = -93 1/3` dus dit wordt `(0,93 1/3)`;
• snijpunt met de `x`-as:
  `f(x) = 0` als `200/(x + 30) = 100` en dus als `x + 30 = 2`.
  Dit geeft `x = -28` en dus als nulpunt `(-28,0)`.
• verticale asymptoot:
  delen door 0 geeft geen reëel getal, dus `x + 30 != 0`;
  als `x = -30` heeft de grafiek een verticale asymptoot.
• horizontale asymptoot:
  als `x` een heel groot (negatief) getal is, dan is `200/(x + 30) ~~ 0`
  en dus wordt dan `f(x) ~~ -100`;
  de horizontale asymptoot is `y = -100`.

‡

Voorbeeld 2

Los op: `40 - 1/(x^2) < 24`.

Antwoord

Voor het oplossen van een ongelijkheid is een grafiek handig.
De functie `y_1 = 40 - 1/(x^2)` is een machtsfunctie want te schrijven als `y_1 = -1x^(-2) + 40`.
De functie ontstaat door transformatie van `y = x^(-2)`:

• lijnvermenigvuldiging met `-1` in de `y`-richting (spiegelen in de `x`-as);
• `40` eenheden in de `y`-richting verschuiven.

De grafiek van `y = x^(-2)` komt goed in beeld met venster `[-4,4] xx [-4,4]`.
De grafiek van `y_1` komt goed in beeld met venster `[-4,4] xx [36,44]`.
Omdat je `y_2 = 24` ook in beeld wilt hebben, kies je `[-4,4] xx [20,44]`.
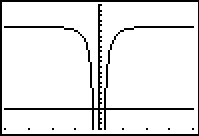Bij `x = 0` zit een verticale asymptoot!

Dan los je op: `40 - 1/(x^2) = 24`.
Je vindt: `x = 0,25 vv x = -0,25`.

De oplossing van de ongelijkheid is `-0,25 < x < 0 vv 0 < x < 0,25`.

‡

Voorbeeld 3

Gegeven is de functie `h` met `h(x) = 200sqrt(x + 30) - 100`.
Leg uit hoe de grafiek van `h` kan ontstaan uit die van `y = x^(1/2)` en bereken de snijpunten met de assen.

Antwoord

`h(x) = 200sqrt(x + 30) - 100` is te schrijven als machtsfunctie `h(x) = 200(x + 30)^(1/2) - 100`.
Dit is een machtsfunctie die ontstaat door transformatie van `y = x^(1/2)`:

• eerst met `-30` verschuiven in de `x`-richting;
• vervolgens vermenigvuldigen met `200` in de `y`-richting (dus t.o.v. de `x`-as);
• tenslotte met `-100` verschuiven in de `y`-richting.

Deze transformaties kun je ook toepassen op de instellingen van het venster van je rekenmachine.
Je ziet de grafiek van `y = x^(1/2)` goed in beeld als het venster is ingesteld op
`[-4,4] xx [-3,5]`.
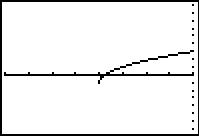Dit wordt na transformatie `[-34,-26] xx [-700,900]`.
Ga na, dat je dan de grafiek van h goed in beeld hebt. Je vindt verder:

• het snijpunt met de `y`-as:
  `h(0) = 200 sqrt(0 + 30) - 100 ~~ 995,45` dus dit wordt `(0; 995,45)`;
• snijpunt met de `x`-as:
  `h(x) = 0` als `200 sqrt(x + 30) - 100 = 0` en dus als `x + 30 = 0,5^2 = 0,25`.
  Dit geeft `x = -29,75` en dus als nulpunt `(-29,75; 0)`;
• asymptoten zijn er nu niet.

‡

Voorbeeld 4

Los op: `40 - root[3](x) < 24`.

Antwoord

Voor het oplossen van een ongelijkheid is een grafiek handig.
De functie `y_1 = 40 - root[3](x)` is een machtsfunctie want te schrijven als `y_1 = -1x^(1/3) + 40`.
De functie ontstaat door transformatie van `y = x^(1/3)`:

• lijnvermenigvuldiging met `-1` in de `y`-richting (spiegelen in de `x`-as);
• `40` eenheden in de `y`-richting verschuiven.

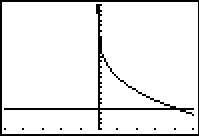
De grafiek van `y = x^(1/3)` komt goed in beeld met venster `[-10,10] xx [-4,4]`.
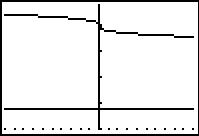De grafiek van `y_1` komt goed in beeld met venster `[-10,10] xx [36,44]`.
Omdat je `y_2 = 24` ook in beeld wilt hebben, kies je `[-10,10] xx [20,44]`.
Je ziet dat het snijpunt van beide grafieken niet in beeld komt, in de `x`-richting moet je veel grotere getallen instellen!
Dus kies je bijvoorbeeld als venster `[-5000,5000] xx [20,44]`.

Dan los je op: `40 - root[3](x) = 24`.
Je vindt: `x = 16^3 = 4096`.

De oplossing van de ongelijkheid is `x > 4096`.

‡

Opgaven

3. Bestudeer Voorbeeld 1. Bekijk zelf de functie `g(x) = 200 - 50/((x - 4)^2)`.
   1. Schrijf het functievoorschrift als machtsfunctie.
   2. Uit welke machtsfunctie van de vorm `y=x^p` kan de grafiek van `g` door transformatie ontstaan? Welke transformaties moet je achtereenvolgens toepassen?
   3. Bepaal de twee asymptoten van de grafiek van `g`.
   4. Bepaal domein en bereik van `g`.
   5. Bereken de snijpunten van de grafiek van `g` met de beide coördinaatassen.


4. Bekijk in Voorbeeld 2 hoe je een ongelijkheid kunt oplossen waarin gebroken functies voorkomen die je kunt schrijven als een machtsfunctie. Los de volgende ongelijkheden op:
   1. `200/(x - 40) >= 50`
   2. `25/((2x + 6)^2) - 100 < 200`


5. Bestudeer Voorbeeld 3. Bekijk zelf de functie `g(x) = 200 - 50sqrt(x + 4)`.
   1. Schrijf het functievoorschrift als machtsfunctie.
   2. Uit welke machtsfunctie van de vorm `y=x^p` kan de grafiek van `g` door transformatie ontstaan? Welke transformaties moet je achtereenvolgens toepassen?
   3. Bepaal domein en bereik van `g`.
   4. Bereken de snijpunten van de grafiek van `g` met de beide coördinaatassen.


6. Bekijk in Voorbeeld 4 hoe je een ongelijkheid kunt oplossen waarin wortelfuncties voorkomen die je kunt schrijven als een machtsfunctie. Los de volgende ongelijkheden op:
   1. `200sqrt(x - 40) >= 50`
   2. `100 - 25sqrt(2x + 6) < 20`


7. Gegeven is de gebroken functie `f` met voorschrift `f(x) = (x+2)/(x+4)`.
   1. Laat zien dat `f(x) = 1 - 2/(x+4)`.
   2. Laat zien dat `f` een machtsfunctie is.
   3. Welke asymptoten heeft de grafiek van `f`?
   4. Bepaal domein en bereik van `f`.


8. Gegeven zijn de functies `f` met `f(x) = 2x sqrt(x) + 4` en `g` met `g(x) = 2x sqrt(x + 4)`.
   1. Waarom is `f` wel een machtsfunctie en `g` niet?
   2. Los op in twee decimalen nauwkeurig: `f(x) >= g(x)`.

Verwerken

9. Gegeven de functie `f` met `f(x) = 40 - 100/((x + 10)^3)`.
   1. Laat zien dat `f` een machtsfunctie is.
   2. Bepaal de asymptoten van de grafiek van `f`.
   3. Schrijf domein en bereik van `f` op.
   4. Bereken algebraïsch het nulpunt van de grafiek van `f`.
   5. Los op in twee decimalen nauwkeurig: `f(x) >= x`.


10. Los de volgende ongelijkheden algebraïsch op.
    1. `16/(x^4) >= 1/2x`
    2. `(2x)/(x-10) + 20 < 100`


11. Gegeven de functie `g` met `g(x) = 20x^2 sqrt(x) - 100`.
    1. Laat zien dat `g` een machtsfunctie is.
    2. Schrijf domein en bereik van `g` op.
    3. Bereken algebraïsch het nulpunt van de grafiek van `g`.
    4. Los op in twee decimalen nauwkeurig: `g(x) >= x`.


12. Los de volgende ongelijkheden algebraïsch op.
    1. `16 root[4](x) >= 1/2x`
    2. `2 sqrt(2x - 40) + 20 < 100`


13. Gegeven zijn de functies `f` en `g` met `f(x) = 10/(x sqrt(x)) + 100` en `g(x) = (10x)/(sqrt(x))`.
    1. Beide functies zijn machtsfuncties. Verklaar op grond van de exponent van deze machtsfunctie waarom de grafiek van `f` altijd dalend en die van `g` stijgend is.
    2. Welke asymptoten hebben deze functies?
    3. Los op in twee decimalen nauwkeurig: `f(x) >= g(x)`.

Toetsen

14. Los de volgende vergelijkingen en ongelijkheden algebraïsch op.
    1. `40 - 5/(x^4) = 0`
    2. `root[3](2x - 10) = 5`
    3. `(2sqrt(x) + 100)/(sqrt(x)) > 12`
    4. `10/((5 - x)^4) >= 0,016`


15. Gegeven zijn de functies `f(x) = 4/(sqrt(10 - x))` en `g(x) = sqrt(10 - x)`.
    1. Geef domein en bereik van `f` en van `g`.
    2. Bereken algebraïsch het snijpunt van de grafieken van `f` en `g`.
    3. Los op: `f(x) >= g(x)`