Kwadratische functies als machtsfuncties

Inleiding

Je gaat nu dieper in op de eigenschappen van machtsfuncties met een exponent 2, kwadraten dus. Kwadratische functies zijn functies waarvan de grafieken kunnen ontstaan door transformaties van de grafiek van y = x2. De grafieken van kwadratische functies zijn parabolen. De eigenschappen van die kwadratische functies kun je gebruiken om kwadratische vergelijkingen op te lossen en om formules bij gegeven parabolen op te stellen.

Je leert nu:

Je kunt al:

Verkennen

Je weet al van alles van kwadratische functies.

> Wat zijn de oplossingen van de vergelijking x2 = 20?
> Hoeveel oplossingen heeft de vergelijking x2 = –1?
> Heeft de ongelijkheid x2 > –1 oplossingen? Zo ja, welke?
> Heeft elke kwadratische vergelijking oplossingen? Hoeveel oplossingen kunnen er zijn?
> Wat weet je allemaal van een kwadratische functie? Maak een overzicht.

Uitleg

Kwadratische functies zijn de functie f(x) = x2 en alle functies waarvan de grafiek door de bekende transformaties uit die van f verkregen kan worden.
Ze hebben daarom de vorm g(x) = a(x – p)2 + q.

Kies bijvoorbeeld a = 2, p = 4 en q = –5 dan krijg je de functie met voorschrift g(x) = 2(x – 4)2 – 5, waarvan de grafiek uit die van f verkregen kan worden door:

De grafiek van g is een dalparabool met top (4, –5) en symmetrieas x = 4. De twee nulpunten bereken je door op te lossen: 2(x – 4)2 – 5 = 0.

Neem je a = –2 in plaats van 2, dan wordt het functievoorschrift h(x) = –2(x – 4)2 – 5.
De grafiek van h is een bergparabool, omdat vermenigvuldiging met een negatief getal een spiegeling t.o.v. de x-as betekent.

‡

Opgaven

  1. Bekijk de Uitleg. Gegeven de functie `f(x)=(1/2)(x-4)^2-4`.
    1. Door welke transformaties kan de grafiek van `f` uit die van `y=x^2` ontstaan?
    2. Schrijf domein en bereik op.
    3. Is hier sprake van een minimum of een maximum? Hoe kun je dat aan het functievoorschrift zien?
    4. Los op: `f(x) < 100`.

  2. Je ziet hier telkens een parabool getekend. Geef het bijbehorende functievoorschrift.

            

Theorie

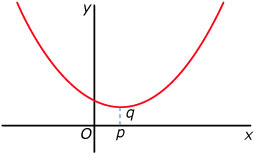
Een functie van de vorm f(x) = a(x – p)2 + q, noem je een kwadratische functie (als a ≠ 0).
De grafiek van elke kwadratische functie ontstaat door een transformatie van de grafiek van y = x2.
De grafiek van elke kwadratische functie is een parabool met top (p, q) en symmetrieas x = p.
Als a > 0 is de grafiek een dalparabool.
Als a < 0 is de grafiek een bergparabool.

De kwadratische vergelijking a(x – p)2 + q = u
kun je herschrijven tot: (x – p)2 = c.

Je vindt die oplossingen door worteltrekken.

‡

Voorbeeld 1

Gegeven is de kwadratische functie
f(x) = 2(x – 1)2 – 5.

Hoe kan de grafiek van f ontstaan uit die van y = x2?
Bepaal ook de top en de symmetrieas van deze grafiek.

Antwoord

Ga na dat de grafiek wordt verkregen door de grafiek van y = x2:

De grafiek is een dalparabool met top (1, –5). De coördinaten van die top zijn direct uit het functievoorschrift af te lezen. De symmetrieas is x = 1.

‡

Voorbeeld 2

Los de vergelijking 2(x – 1)2 – 5 = 3 op.

Antwoord

De grafiek van f(x) = 2(x – 1)2 – 5 heb je in Voorbeeld 1 gemaakt.
Deze vergelijking oplossen doe je systematisch:

2(x – 1)2 – 5 = 3                        5 optellen aan beide kanten
       2(x – 1)2 = 8                       deel door 2
         (x – 1)2 = 4                        worteltrekken
x – 1 = 2  V  x – 1 = –2             1 optellen
      x = 3  V  x = –1

Je ziet ook meteen aan de grafiek van f, dat de vergelijking 2(x – 1)2 – 5 = –8 geen oplossingen heeft.

En ook dat de vergelijking 2(x – 1)2 – 5 = –5 precies één oplossing heeft, namelijk x = 1.

‡

Voorbeeld 3

Los de ongelijkheid –5(x + 3)2 – 17 ≥ –47 op.

Antwoord

Eerst los je de bijbehorende vergelijking systematisch op:

–5(x + 3)2 – 17 = –47            beide zijden 17 optellen
         –5(x + 3)2 = –30            deel beide kanten door –5
             (x + 3)2 = 6                 worteltrekken
`x + 3 = sqrt(6) vv x = 3 = -sqrt(6)`    3 aftrekken en benaderen
  x = –0,55  V  x = –5,45

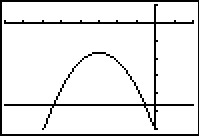
Nu bekijk je de grafieken van y1 = –5(x + 3)2 – 17 en y2 = –47.
Uit de grafiek lees je af dat `[-3 - sqrt(6), -3 + sqrt(6)]` de oplossing is van deze ongelijkheid.
Dit interval is bij benadering gelijk aan [–5,45; –0,55].

‡

Voorbeeld 4

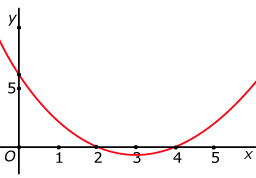
De nulpunten van de kwadratische functie f zijn (2, 0) en (4, 0). Het snijpunt met de y-as is (0, 6).

Welk functievoorschrift heeft deze functie?

Antwoord

De grafiek van f is een parabool waarvan de symmetrieas een verticale lijn door (3, 0) is.
Dus is f(x) = a(x – 3)2 + q.

Nu gaat de grafiek door (0, 6) dus f(0) = 6: 9a + q = 6.

De grafiek gaat ook door (2, 0) dus f(2) = 0: a + q = 0.

Uit de onderste vergelijking volgt: q = –a.
Vul je dit in de bovenste vergelijking in, dan vind je: 9a – a = 6.
En dus: a = 0,75.
Omdat q = –a is: q = –0,75.

Het functievoorschrift wordt: f(x) = 0,75(x – 3)2 – 0,75.

‡

Voorbeeld 5

Bij een tenniswedstrijd wordt de bal vanaf 0,5 m boven de baseline in de lengterichting van het veld over het net geslagen. Het hoogste punt van de (ongeveer) parabolische baan ligt op 2 m voor het net en 1,5 m boven het veld. Het 1 m hoge net staat in het midden van de lengte van het veld, die ongeveer 24 m bedraagt.
Toon door berekening aan dat de bal "in" is.

Antwoord

Breng een geschikt assenstelsel aan, zie figuur.
De top van de parabool is dan (10;1,5) en hij moet ook door (0;0,5) gaan.

Bij deze parabool hoort een formule van de vorm h = a(x – 10)2 + 1,5.
(0;0,5) invullen geeft a = –0,01.
Dus wordt de baan van de bal (ongeveer) beschreven door h = –0,01(x – 10)2 + 1,5.

De bal komt op de grond als h = 0. Ga na, dat dan `x = 10 + sqrt(150)`.

‡

Opgaven

  1. Bekijk Voorbeeld 1. Gegeven de functie `f(x) = 2(x + 1)^2 - 3`.
    1. Door welke transformaties kan de grafiek van `f` uit die van `y = x^2` ontstaan?
    2. Schrijf domein en bereik op.
    3. Bepaal de uiterste waarde van `f`.
    4. Los op: `f(x) >= 100`.

  2. Als je de grafiek van `y=x^2` verschuift en ten opzichte van de `x`-as vermenigvuldigt, krijg je een grafiek waarvan het functievoorschrift als volgt te schrijven is: `f(x) = a(x-p)^2 + q`.
    1. Hoe kun je aan het functievoorschrift zien of de grafiek een bergparabool of een dalparabool is? Geeft dit ook aan of de grafiek een maximum of minimum heeft?
    2. Hoe kun je aan het functievoorschrift zien hoe groot het maximum of minimum is?
    3. Hoe kun je aan het functievoorschrift zien welke waarde van `x` je in moet vullen om het maximum of minimum te krijgen?
    4. Schrijf domein en bereik van deze functie op.

  3. Bestudeer eerst Voorbeeld 2.
    Los de volgende vergelijkingen algebraïsch op. Laat eventuele wortels staan.
    1. `x^2 = 100`
    2. `(x - 4)^2 = 64`
    3. `-3(x + 1)^2 = -75`
    4. `3(x + 2)^2 - 3 = 27`
    5. `2x^2 - 7 = 0`

  4. Los de volgende ongelijkheden algebraïsch op. In Voorbeeld 3 zie je hoe je dit kunt doen.
    1. `(x - 4)^2 < 10`
    2. `-2(x +3 )^2 + 10 < 4`
    3. `3(x - 5)^2 - 2 >= 10`

  5. In Voorbeeld 4 zie je hoe je een voorschrift opstelt van een kwadratische functie als de drie snijpunten van de grafiek met de assen zijn gegeven.
    Stel zelf een voorschrift op van de kwadratische functie `f` door `(-2,0)`, `(0,2)` en `(4,0)`.

  6. In Voorbeeld 5 wordt de baan van een tennisbal beschreven met een kwadratische functie.
    1. De baan is alleen ongeveer parabolisch. Waarom is hij zeer waarschijnlijk niet precies parabolisch?
    2. Laat zien dat inderdaad `a = -0,01`.
    3. Bereken nu de twee nulpunten van de kwadratische functie die de baan van de tennisbal (ongeveer) beschrijft. Laat zien dat de bal inderdaad "in" is.

Verwerken

  1. De grafiek van de functie `f(x) = 2(x + 8)^2 - 8` ontstaat door transformatie van de grafiek van `y = x^2`.
    1. Welke transformaties moet je dan toepassen?
    2. Verander de volgorde van laatste twee transformaties en teken de grafiek van de functie `g` die zo ontstaat. Waarom is de volgorde van die transformatie dus belangrijk?

  2. Bekijk de grafiek van `f(x) = -2(x + 4)^2 + 5`
    1. Geef het maximum, danwel minimum van `f` en de waarde van `x` waarvoor je deze extreme waarde krijgt.
    2. Los de vergelijking `-2(x + 4)^2 + 5 = -5` op.
    3. Los op: `f(x) = 5`
    4. Los op: `f(x) = 10`
    5. Los op: `f(x) > -3`
    6. Los op: `f(x) < 0`
    7. Los op: `f(x) < 20`

  3. Gegeven is de functie `f(x) = -3(x + 2)^2 + 10`.
    1. Op welk interval is deze functie dalend?
    2. Is de functie op de rest van het domein dus stijgend?
    3. Bereken de nulpunten van `f`.

  4. Bekijk de grafiek van de functie `f(x) = 2(x - 1)^2 - 3`.
    1. Los algebraïsch op: `2(x - 1)^2 - 3 = 0`
    2. Teken de grafiek van `f` door elke transformatie vanuit `y=x^2` te tekenen.
    3. Vergelijk je antwoorden van a en b. Ga na waar elke transformatie te vinden is in de oplossing bij a.

  5. Los de onderstaande ongelijkheden algebraïsch op.
    1. `5(x - 1)^2 - 9 > 4`
    2. `5 - x^2 > -21`
    3. `3(x - 1)^2 < 40`
    4. `-4(x + 80)^2 - 40 < -100`

  6. Een basketballer maakt een driepunter zonder het bord te raken (hij gooit de bal dus in één keer door de ring van de basket). De baan van de bal is (ongeveer) een parabool, zie figuur. Het hoogste punt van de baan is gegeven. De speler laat de bal op 2,5 m boven de grond los.



    1. Stel een formule op voor de functie `h(x)` die de baan van de bal beschrijft.
    2. De ring van de basket hangt op 3,05 m boven de grond. Hoe ver staat de speler vanaf (het midden van) de ring van de basket?

  7. Gegeven is de functie `f(x) = -1/2(x - 3)^2 + c`. Hierin is `c` een nog onbekende constante.
    1. Welke extreme waarde heeft deze functie `f`?
    2. Voor welke waarden van `c` heeft de functie `f` twee nulpunten? Licht je antwoord toe.
    3. Voor welke waarden van `c` heeft de functie `f` geen snijpunten met de lijn `y = 4`?
    4. Voor welke waarden van `c` ligt de top van de grafiek van `f` op de lijn `y = 4x - 5`?

Toetsen

  1. Bepaal bij de volgende functies de top van de grafiek.
    1. `f(x) = -2x^2 - 2`
    2. `g(x) = 100(x - 4)^2 + 8`
    3. `h(x) = -(x + 5)^2`

  2. Los de volgende vergelijkingen en ongelijkheden algebraïsch op. Laat eventuele wortels staan.
    1. `3(x - 5)^2 - 5 = -2`
    2. `3(x - 5)^2 - 5 = -5`
    3. `-2(x + 4)^2 + 3 = 1`
    4. `2(x + 2)^2 > 10`
    5. `-(x + 4)^2 < -3`
    6. `(x + 4)^2 - 5 < -3`

  3. Stel een voorschrift op van de kwadratische functie `f` door de punten `(10,0)`, `(20,0)` en `(0,30)`.