Kwadratische functies als machtsfuncties

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Kwadratische functies als machtsfuncties > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Kwadratische functies als machtsfuncties > Uitleg

Lees eerst de Uitleg goed door.

Opgaven

1. Bekijk de Uitleg. Gegeven de functie `f(x)=(1/2)(x-4)^2-4`.
   1. Door welke transformaties kan de grafiek van `f` uit die van `y=x^2` ontstaan?
   2. Schrijf domein en bereik op.
   3. Is hier sprake van een minimum of een maximum? Hoe kun je dat aan het functievoorschrift zien?
   4. Los op: `f(x) < 100`.


2. Je ziet hier telkens een parabool getekend. Geef het bijbehorende functievoorschrift.
   
           
   
   

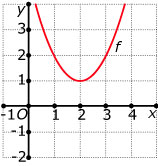
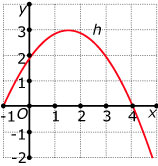
Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Machtsfuncties > Kwadratische functies als machtsfuncties > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

3. Bekijk Voorbeeld 1. Gegeven de functie `f(x) = 2(x + 1)^2 - 3`.
   1. Door welke transformaties kan de grafiek van `f` uit die van `y = x^2` ontstaan?
   2. Schrijf domein en bereik op.
   3. Bepaal de uiterste waarde van `f`.
   4. Los op: `f(x) >= 100`.


4. Als je de grafiek van `y=x^2` verschuift en ten opzichte van de `x`-as vermenigvuldigt, krijg je een grafiek waarvan het functievoorschrift als volgt te schrijven is: `f(x) = a(x-p)^2 + q`.
   1. Hoe kun je aan het functievoorschrift zien of de grafiek een bergparabool of een dalparabool is? Geeft dit ook aan of de grafiek een maximum of minimum heeft?
   2. Hoe kun je aan het functievoorschrift zien hoe groot het maximum of minimum is?
   3. Hoe kun je aan het functievoorschrift zien welke waarde van `x` je in moet vullen om het maximum of minimum te krijgen?
   4. Schrijf domein en bereik van deze functie op.


5. Bestudeer eerst Voorbeeld 2.
   Los de volgende vergelijkingen algebraïsch op. Laat eventuele wortels staan.
   1. `x^2 = 100`
   2. `(x - 4)^2 = 64`
   3. `-3(x + 1)^2 = -75`
   4. `3(x + 2)^2 - 3 = 27`
   5. `2x^2 - 7 = 0`


6. Los de volgende ongelijkheden algebraïsch op. In Voorbeeld 3 zie je hoe je dit kunt doen.
   1. `(x - 4)^2 < 10`
   2. `-2(x +3 )^2 + 10 < 4`
   3. `3(x - 5)^2 - 2 >= 10`


7. In Voorbeeld 4 zie je hoe je een voorschrift opstelt van een kwadratische functie als de drie snijpunten van de grafiek met de assen zijn gegeven.
   Stel zelf een voorschrift op van de kwadratische functie `f` door `(-2,0)`, `(0,2)` en `(4,0)`.
   


8. In Voorbeeld 5 wordt de baan van een tennisbal beschreven met een kwadratische functie.
   1. De baan is alleen ongeveer parabolisch. Waarom is hij zeer waarschijnlijk niet precies parabolisch?
   2. Laat zien dat inderdaad `a = -0,01`.
   3. Bereken nu de twee nulpunten van de kwadratische functie die de baan van de tennisbal (ongeveer) beschrijft. Laat zien dat de bal inderdaad "in" is.

Verwerken

9. De grafiek van de functie `f(x) = 2(x + 8)^2 - 8` ontstaat door transformatie van de grafiek van `y = x^2`.
   1. Welke transformaties moet je dan toepassen?
   2. Verander de volgorde van laatste twee transformaties en teken de grafiek van de functie `g` die zo ontstaat. Waarom is de volgorde van die transformatie dus belangrijk?


10. Bekijk de grafiek van `f(x) = -2(x + 4)^2 + 5`
    1. Geef het maximum, danwel minimum van `f` en de waarde van `x` waarvoor je deze extreme waarde krijgt.
    2. Los de vergelijking `-2(x + 4)^2 + 5 = -5` op.
    3. Los op: `f(x) = 5`
    4. Los op: `f(x) = 10`
    5. Los op: `f(x) > -3`
    6. Los op: `f(x) < 0`
    7. Los op: `f(x) < 20`


11. Gegeven is de functie `f(x) = -3(x + 2)^2 + 10`.
    1. Op welk interval is deze functie dalend?
    2. Is de functie op de rest van het domein dus stijgend?
    3. Bereken de nulpunten van `f`.


12. Bekijk de grafiek van de functie `f(x) = 2(x - 1)^2 - 3`.
    1. Los algebraïsch op: `2(x - 1)^2 - 3 = 0`
    2. Teken de grafiek van `f` door elke transformatie vanuit `y=x^2` te tekenen.
    3. Vergelijk je antwoorden van a en b. Ga na waar elke transformatie te vinden is in de oplossing bij a.


13. Los de onderstaande ongelijkheden algebraïsch op.
    1. `5(x - 1)^2 - 9 > 4`
    2. `5 - x^2 > -21`
    3. `3(x - 1)^2 < 40`
    4. `-4(x + 80)^2 - 40 < -100`


14. Een basketballer maakt een driepunter zonder het bord te raken (hij gooit de bal dus in één keer door de ring van de basket). De baan van de bal is (ongeveer) een parabool, zie figuur. Het hoogste punt van de baan is gegeven. De speler laat de bal op 2,5 m boven de grond los.
    
    
    
    
    1. Stel een formule op voor de functie `h(x)` die de baan van de bal beschrijft.
    2. De ring van de basket hangt op 3,05 m boven de grond. Hoe ver staat de speler vanaf (het midden van) de ring van de basket?


15. Gegeven is de functie `f(x) = -1/2(x - 3)^2 + c`. Hierin is `c` een nog onbekende constante.
    1. Welke extreme waarde heeft deze functie `f`?
    2. Voor welke waarden van `c` heeft de functie `f` twee nulpunten? Licht je antwoord toe.
    3. Voor welke waarden van `c` heeft de functie `f` geen snijpunten met de lijn `y = 4`?
    4. Voor welke waarden van `c` ligt de top van de grafiek van `f` op de lijn `y = 4x - 5`?

Toetsen

16. Bepaal bij de volgende functies de top van de grafiek.
    1. `f(x) = -2x^2 - 2`
    2. `g(x) = 100(x - 4)^2 + 8`
    3. `h(x) = -(x + 5)^2`


17. Los de volgende vergelijkingen en ongelijkheden algebraïsch op. Laat eventuele wortels staan.
    1. `3(x - 5)^2 - 5 = -2`
    2. `3(x - 5)^2 - 5 = -5`
    3. `-2(x + 4)^2 + 3 = 1`
    4. `2(x + 2)^2 > 10`
    5. `-(x + 4)^2 < -3`
    6. `(x + 4)^2 - 5 < -3`


18. Stel een voorschrift op van de kwadratische functie `f` door de punten `(10,0)`, `(20,0)` en `(0,30)`.