Eigenschappen van machtsfunties
Inleiding
Bij functies van de vorm `f(x) = x^p` hangt het verloop van de functie af van de waarde van `p`.
Voor bijvoorbeeld `p=2` krijg je een kwadratische functie met als grafiek een parabool. Deze functie is dalend voor `x < 0` en stijgend voor `x > 0`.
Voor `p = 1` krijg je een lineaire functie, die stijgend is voor elke waarde van `x`.
In dit onderdeel zul je zien dat voor negatieve en gebroken waarden van `p` je machtsfuncties krijgt met weer een ander karakter.
Je leert nu:
- het verband tussen de waarde van p en het verloop van de grafiek van f(x) = xp kennen;
- het verloop van functies die door transformaties van f(x) = xp ontstaan.
Je kunt al:
- werken met functies en grafieken, ook met de grafische rekenmachine;
- vergelijkingen met machten oplossen.
Verkennen
Machtsfuncties hebben de vorm `f(x) = c * x^p`. Je kunt de bijbehorende grafieken bekijken met de grafische rekenmachine. Je kiest dan voor `c` en voor `p` getallen.
Neem voor het gemak steeds `c=1` en neem voor `p` een geheel getal.
> Welke machtsfuncties hebben een minimum? Wat zijn daar de coördinaten van?
> Zijn er machtsfuncties die overal op hun domein stijgend zijn? Zo ja, geef dan een paar voorbeelden.
> Hoe kun je er voor zorgen dat de machtsfunctie `f(x) = x^p` dalend is voor positieve waarden van `x`?
Neem nu ook gebroken getallen voor `p`.
> Welke verschillen zijn er tussen de grafiek bij `p = 1/2` en die bij `p = 1/3`?
> Bekijk de grafiek bij `p = 2/3`. Wat is er bij x = 0 aan de hand?
> Als `p` een decimaal getal is, mag je alleen positieve waarden voor `x` toelaten. Waarom zou dat zijn?
Uitleg
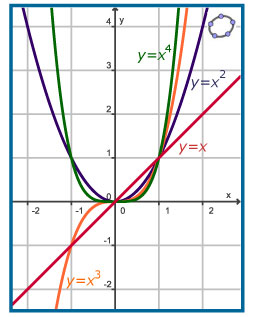
Je ziet hiernaast de grafieken van `f(x) = x^p` voor enkele positieve gehele waarden van `p`.
Merk op:
-
Als p een positief even getal is, geldt:
- `text(D)_f = [0, rarr:)` en `text(B)_f = [0, rarr:)`;
- de grafiek dalend is als `x < 0` en stijgend als `x > 0`;
- de vergelijking `x^p = a` twee oplossingen heeft als `a > 0`,
één oplossing heeft als `a = 0` en geen oplossingen heeft als `a < 0`.
-
Als p een positief oneven getal is, geldt:
- `text(D)_f = [0, rarr:)` en `text(B)_f = RR`;
- de grafiek stijgend is voor elke waarde van `x` (behalve 0);
- de vergelijking `x^p = a` één oplossing heeft voor elke waarde van `a`.
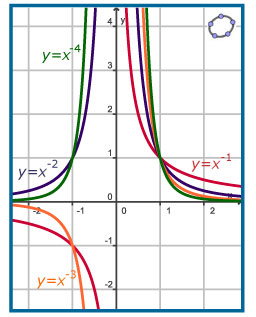
Je ziet hiernaast de grafieken van `f(x) = x^p` voor enkele negatieve gehele waarden van `p`.
Merk op:
-
Als p een negatief even getal is, geldt:
- `text(D)_f = (:larr, 0:) uu (:0, rarr:)` en `text(B)_f = (:0, rarr:)`;
- de grafiek stijgend is als `x < 0` en dalend als `x > 0`;
- de vergelijking `x^p = a` twee oplossingen heeft als `a > 0` en geen oplossingen heeft als `a <= 0`.
-
Als p een negatief oneven getal is, geldt:
- `text(D)_f = (:larr, 0:) uu (:0, rarr:)` en `text(B)_f = (:larr, 0:) uu (:0, rarr:)`;
- de grafiek dalend is voor elke waarde van `x` (behalve 0);
- de vergelijking `x^p = a` één oplossing heeft voor elke waarde van `a` behalve `a=0`.
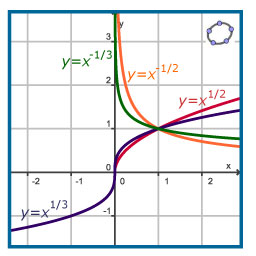
Je ziet hiernaast grafieken van `f(x) = x^(1/p)` voor enkele gehele waarden van `p`.
Merk op:
-
Als `p > 1` geldt:
- `text(D)_f = [0, rarr:)` en `text(B)_f = [0, rarr:)`;
- de grafiek stijgend is voor alle `x` uit het domein;
- de grafiek gaat door `(0, 0)` en `(1, 1)`;
- de vergelijking `f(x) = a` één oplossing heeft als `a >= 0`.
-
Als `p < -1` geldt:
- `text(D)_f = (:0, rarr:)` en `text(B)_f = (:0, rarr:)`;
- de grafiek dalend is voor elke `x` uit het domein;
- de grafiek horizontale asymptoot `y=0` en verticale asymptoot `x=0` heeft;
- de vergelijking `f(x)=a` één oplossing heeft als `a > 0`.
Kijk nog eens goed of je grafische rekenmachine dezelfde grafieken geeft.
Er kunnen verschillen zijn. Merk ook op dat de grafiek in de buurt van x = 0 niet altijd helemaal netjes wordt gemaakt.
‡
Opgaven
-
Bekijk de Uitleg, pagina 1.
Maak grafieken van de functies: `f(x)=x^4`, `g(x)=x^3`, `h(x)=x^2` en `j(x)=x`.
- Voor welke waarden van `x` geldt: `f(x) = g(x)`? En `f(x) > g(x)`?
- Voor welke waarden van `x` geldt: `f(x) = h(x)`? En `f(x) > h(x)`?
- Voor welke waarden van `x` geldt: `f(x) = j(x)`? En `f(x) > j(x)`?
- Om de voorgaande vragen in het algemeen te kunnen beantwoorden, kijk je naar twee functies: `f(x)=x^p` en `g(x)=x^q`, waarbij `p` een even positief getal is en `q` een oneven positief getal.
Neem de tabel over en vul hem in.
| `x < -1` | `-1 < x < 0` | `0 < x < 1` | `x > 1` |
| `p < q` |
|
|
|
|
| `p > q` |
|
| `f(x) < g(x)` |
|
-
Bekijk de functies `k(x)=x^5` en `l(x)=x^6`.
- Maak een schets van de grafieken van `k(x)` en `l(x)`. Controleer je antwoord met de grafische rekenmachine.
- Voor welke waarden van `x` geldt `x^6 = 10`? Los op: `x^6 < 10`.
- En voor welke waarde van `x` geldt `x^5 = 10`? Los op: `x^5 > 10`.
-
Bekijk de Uitleg, pagina 2.
Maak grafieken van de functies: `k(x)=x^(-1)` en `l(x)=x^(-2)`.
- Welke asymptoten hebben deze functies? En waarom?
- Voor welke waarden van `x` geldt `k(x)=l(x)`? Los op: `k(x) < l(x)`.
- Los de volgende vergelijkingen op:
- `x^(-1)=0,005` en `x^(-2)=0,005`
- `x^(-1)=5000` en `x^(-2)=5000`
- Voor welke waarden van `x` geldt `x^(-1) < 0,005`?
- Voor welke waarden van `x` geldt `x^(-1) > 5000`?
- Voor welke waarden van `x` geldt `x^(-2) < 0,005`?
- Voor welke waarden van `x` geldt `x^(-2) > 5000`?
-
Bekijk de Uitleg, pagina 3.
Maak grafieken van de functies: `a(x)=x^(-1/2)`, `b(x)=x^(1/2)`, `c(x)=x` en `d(x)=x^(1/3)`
- Voor welke waarden van `x` geldt `a(x) < b(x)`?
- Voor welke waarden van `x` geldt `d(x) < b(x)`?
- Voor welke waarden van `x` geldt `d(x) < c(x)`?
- Maak in één figuur een schets van de grafieken van `d(x)` en `f(x)=x^(1/4)`. Controleer je schets met de grafische rekenmachine.
- Voor welke waarden van `x` geldt `x^(1/4) > 4`?
Theorie
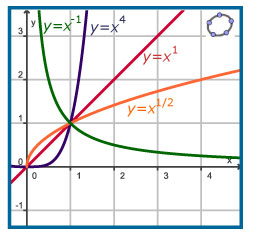
Je ziet hier enkele grafieken van de machtsfunctie `f(x) = x^p` voor enkele verschillende waarden van `p`. Eigenschappen voor `x > 0` zijn:
- `p > 1`: de grafiek gaat door `(0, 0)` en `(1, 1)` en stijgt steeds sneller.
- `p = 1`: f is een lineaire functie door `(0, 0)` en `(1, 1)`.
- `0 < p < 1`: de grafiek gaat door `(0, 0)` en `(1, 1)` en stijgt steeds langzamer.
- `p < 0`: de functie is niet gedefinieerd voor `x = 0`, de grafiek gaat door `(1, 1)` en daalt steeds langzamer, de `x`-as en de `y`-as zijn asymptoten van de grafiek.
Voor `x < 0` bestaat de functie alleen als `p` een geheel getal is (of als `p` een breuk is met een oneven noemer, zoals 1/3, 2/3, 1/5, 2/5, etc). Afhankelijk van het even of oneven zijn van `p` is de grafiek daar dalend of stijgend.
De vergelijking `x^p = a` heeft één oplossing als `a > 0` en `p` geen even geheel getal (ongelijk 0) is, want dan zijn het er twee.
De vergelijking `x^p = a` heeft één oplossing als `a < 0` en `p` een oneven geheel getal (ongelijk 0) is.
‡
Voorbeeld 1
Los op: `3x^(3/2) < 12`.
Antwoord
Beide kanten delen door 3 geeft: `x^(3/2) < 4`.
Los nu eerst op `x^(3/2) = 4`.
Oplossing: `x = 4^(2/3) ~~ 2,52`.
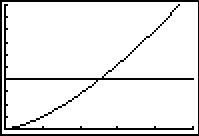
Maak nu de grafiek van `f(x) = x^(3/2)` op de grafische rekenmachine.
Merk op dat `text(D)_f = [0,rarr:)`.
De vergelijking heeft inderdaad maar één oplossing.
Nu lees je de (benaderde) oplossing van de ongelijkheid uit de grafiek af: `0 <= x < 2,52`.
‡
Voorbeeld 2
Gegeven is de functie `f(x) = 2(x - 4)^3 - 10`.
Los op: `f(x) = 20`.
Antwoord
Functie `f` kan door transformatie ontstaan uit de machtsfunctie `y_1 = x^3`. Eerst 4 verschuiven in de positieve `x`-richting (dus t.o.v. de `y`-as), dan vermenigvuldigen met `2` in de `y`-richting en tenslotte 10 verschuiven in de negatieve `y`-richting.
Om `f(x) = 20` op te lossen, moet je stap voor stap terugrekenen:
`2(x - 4)^3 - 10 = 20` 10 optellen
`2(x - 4)^3 = 30` door 2 delen
`(x - 4)^3 = 15` terug vanuit derdemacht
`x - 4 = 15^(1/3)` 4 optellen
`x = 15^(1/3) + 4 ~~ 6,47`
‡
Voorbeeld 3
Los op: `1/(x^4) > 4`.
Antwoord
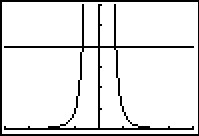
Omdat `f(x) = 1/(x^4) = x^(-4)` is ook hier sprake van een machtsfunctie.
Maak eerst de grafiek van `f` en de lijn `y_2 = 4` op je grafische rekenmachine.
Los nu op: `x^(-4) = 4`.
Oplossing: `x = 4^(-1/4) vv x = -4^(-1/4)`, dus `x = 0,5 vv x = -0,5`.
In de grafiek is de oplossing van de ongelijkheid af te lezen:
`-0,5 < x < 0 vv 0 < x < 0,5`.
Merk op dat je `x=0` uitzondert omdat voor deze waarde de functie `f` niet gedefinieerd is.
‡
| soort |
m (kg) |
Z (L) |
| muis |
0,20 |
0,19 |
| rat |
1,10 |
0,75 |
| kat |
5,80 |
2,62 |
| hond |
11,5 |
4,38 |
| mens |
76,1 |
18,0 |
| paard |
605,0 |
85,4 |
Voorbeeld
De Amerikaanse veearts en onderzoeker Max Kleiber ontdekte in 1932 dat het zuurstofverbruik Z (in L) van verschillende soorten zoogdieren recht evenredig is met een macht van de massa `m` (in kg). In de tabel vind je enkele bijpassende gegevens. Stel een formule op voor `Z` afhankelijk van `m`.
Antwoord
Deze machtsfunctie heeft de vorm `Z = c * m^p`, waarin `c` en `p` nog te berekenen zijn.
Je hebt daartoe genoeg aan de gegevens van twee diersoorten, bijvoorbeeld:
- paard: `Z = 85,4` en `m = 605,0` geeft: `85,4 = c * 605,0^p`
- muis: `Z = 0,19` en `m = 0,20` geeft: `0,19 = c * 0,20^p`
Met de balansmethode vind je dan: `(85,4)/(0,19) = (605,0^p)/(0,20^p)` en dus `449,47 ~~ 3025^p`.
Zo'n exponentiële vergelijking los je met de GR op: `p ~~ 0,76`.
En nu vind je door invullen ook `c ~~ 0,66`.
Het resultaat komt dicht bij de door Kleiber gevonden formule `Z = 0,7 * m^0,75`.
‡
Opgaven
-
In Voorbeeld 1 zie je hoe je de ongelijkheid `3x^(3/2) < 12` oplost.
-
Los zelf eerst de vergelijking `3x^(3/2) = 12` algebraïsch op.
-
In het voorbeeld wordt daarbij een macht met exponent `2/3` gebruikt. Licht die stap toe.
Heb je dat zelf ook gedaan?
-
Los op dezelfde manier algebraïsch op: `15x^(3/5) < 180`.
Geef je eindantwoord in twee decimalen nauwkeurig.
-
Bekijk de functie `f(x)=3(x+1)^3 - 5`.
- Beschrijf in de juiste volgorde welke transformaties er nodig zijn vanuit `y=x^3` om tot de functie `f(x)` te komen.
Geef elke keer aan wat er met de grafiek gebeurt als je deze transformatie toepast.
Werk eventueel met de applet in Voorbeeld 2.
- Los op: `f(x) < 10`.
-
Los de volgende vergelijkingen en ongelijkheden algebraïsch op. Bekijk eventueel eerst Voorbeeld 3.
Controleer je antwoord met de grafische rekenmachine.
Houd ook rekening met het domein van de verschillende functies.
- `x^2 < sqrt(x)`
- `1/(x^4) = 81`
- `1/(x^3) < 27`
- `1/(x^3) < 30`
- `x^5 < x^4`
- `x^6 < x^4`
-
Gegeven is de functie `f(x) = 2(x + 1)^(-2) - 4`.
- Welke asymptoten heeft de grafiek van `y=x^(-2)`?
- Beschrijf welke transformaties je moet uitvoeren op de grafiek van `y=x^(-2)` om die van `f` te krijgen.
- Welke asymptoten heeft de grafiek van `f`?
- Schrijf domein en bereik van `f` op.
- Los op: `f(x) < 10`.
-
Bestudeer Voorbeeld 4 over de formule van Kleiber.
Er wordt een formule opgesteld voor het verband tussen het zuurstofverbruik `Z` in L en de massa `m` in kg bij zoogdieren.
Daarbij wordt gebruik gemaakt van de gegevens van de muis en het paard.
-
Stel de formule op uitgaande van de gegevens van de rat en de mens.
Vind je dezelfde formule?
-
Bereken met de formule van Kleiber het zuurstofverbruik van een koe van 1000 kg.
Verwerken
-
In een grootwinkelbedrijf onderzoekt de marktafdeling hoe de tomatenverkoop afhangt van de prijs. Iemand beweert dat dan de volgende formule geldt: `a=500/p`. Hierin is `a` de verkoop per dag in kg en `p` de prijs per kg in euro.
- Schrijf de formule zo, dat blijkt dat de afzet recht evenredig is met de macht van de prijs.
- Teken de grafiek met de grafische rekenmachine voor de prijs tussen € 1,00 en € 5,00 per kg. Als de prijs verdubbeld wordt, wordt de afzet dan meer of minder dan de helft? Hoe kun je dat aan de grafiek direct zien?
- Het bedrijf heeft een voorraad van `300` kg tomaten. Bereken de prijs waarbij de voorraad binnen een dag is verkocht. Geef ook de formule waarmee je dit direct kunt berekenen.
- Hoe groot is de verkoop bij een prijs van € 0,01? En bij € 100,00? Geef zelf aan wat dit betekent voor de bruikbaarheid van deze formule.
-
Gegeven is de functie `f(x) = 3/(sqrt(x - 1)) + 5`.
- Leg uit dat de grafiek van deze functie kan ontstaan door transformatie van de grafiek `y=x^(-1/2)`.
- Welke transformaties moet je toepassen om de grafiek van `f` te krijgen?
- Schrijf domein en bereik van `f` op.
- Los op: `f(x) <= 10`.
-
Bekijk de grafieken van de functies `f(x) = -5 + 2sqrt(x - 3)` en `g(x) = sqrt(x)`.
- Schrijf `f` en `g` als machtsfunctie en beschrijf hoe de grafiek van `f(x)` vanuit die van `g(x)` kan ontstaan.
- Geef het domein en bereik van zowel `f` als `g`.
- Los op: `f(x) >= 100`.
-
Gegeven is de functie `f(x)=100/((x-10)^2) + 25`.
- Laat zien, dat de grafiek van deze functie kan ontstaan uit een machtsfunctie.
Schrijf bijbehorende transformaties op.
- Welke asymptoten heeft de grafiek van `f`?
- Schrijf domein en bereik van `f` op.
- Los op: `f(x) <= 50`.
-
Een functie die door transformatie uit een machtsfunctie ontstaat is: `h(x) = a(x - b)^c + d`.
- Voor welke waarden van `c` heeft de functie een maximum of minimum?
- Waar hangt het van af of het een maximum of minimum is?
- Hoe kun je uit deze formule aflezen waar de top zich bevindt? Geef de coördinaten van deze top.
Testen
-
Geef van de volgende machtsfuncties
- het domein en het bereik;
- de intervallen waarop de grafiek dalend dan wel stijgend is;
- het maximum of minimum (voor zover van toepassing);
- de asymptoten (voor zover van toepassing)
- `a(x) = x^5` en `b(x) = x^6`
- `c(x) = x^(-3)` en `d(x) = x^(-4)`
- `e(x) = x^(1/4)` en `f(x) = x^(3 1/2)`
-
Los de volgende vergelijkingen en ongelijkheden algebraïsch op.
- `2(x + 4)^4 - 10 = 500`
- `10 - 2 sqrt(x - 4) > 6`
- `root4x < 20`
- `2(x + 1)^3 > 20`
- `5 + 2sqrt(x - 3) < 20`