Werken met machten

Inleiding

In een vlak landschap wordt het verband tussen de kijkafstand a (in m) en de hoogte h (in m) gegeven door de formule `a = 3573 * h^(1/2)`.
Dit is een voorbeeld van een zogenaamd machtsverband, want de variabele h moet tot de macht 0,5 worden verheven. Je kunt ook zeggen dat h een machtsfunctie is van a. Je maakt in dit onderdeel met machtsfuncties kennis.

Je leert nu:

Je kunt al:

Verkennen

Bekijk het verhaal van de kijkafstand bij de Inleiding.

> Welke van de volgende beweringen is waar?

> Kun je een manier bedenken om zelf die formule af te leiden? (Ga er van uit dat de aarde een zuivere bol is met een straal van 6378 km.)

Uitleg

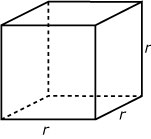
De inhoud van een kubus met ribben van lengte `r` is: `I = r * r * r = r^3`.
Dit is een typisch voorbeeld van een machtsfunctie: de variabele `r` moet tot de derde macht worden verheven om een functiewaarde te vinden. Als `r=5`, dan is `I=5^3=125`.

Al in de Oudheid vroegen de Grieken zich af hoe groot nu de ribbe is van een kubus die een inhoud heeft die precies het dubbele is van de gegeven inhoud. In ons geval: "Hoe groot is de ribbe van een kubus met een inhoud van 250?"
De oplossing van deze vraag is tegelijk eenvoudig als heel erg moeilijk. Want net als bij terugrekenen van uit een kwadraat door worteltrekken kun je terugrekenen vanuit een derde macht. Dat heet dan een derde machts wortel.
De gevraagde oplossing is dan `r = root[3](250)`.

Het moeilijke hieraan is dat deze oplossing geen getal is dat je in alle decimalen kunt berekenen; je kunt het slechts benaderen (door inklemmen). Je rekenmachine kan dit snel voor je doen: `r = root[3](250) ~~ 6,299605` als het in zes decimalen nauwkeurig moet.

Een andere schrijfwijze voor de oplossing van `r^3=250`r3 = 250 is: `r = 250^(1/3)`.
Immers: `(250^(1/3))^3 = 250`. Je ziet: `root[3](250) = 250^(1/3)`.

Kijk je naar het gewicht van de kubus, dan moet je rekening houden met de soortelijke massa. Dat is de massa (in kilogram) van 1 dm3.
De soortelijke massa van bijvoorbeeld een massief ijzeren kubus is 7,87 kg.

Voor het gewicht van deze kubus geldt: G = 7,87 · r3, waarin r is uitgedrukt in dm.

Dit is opnieuw een voorbeeld van een machtsfunctie:
G is recht evenredig met een macht van r.

‡

Opgaven

  1. Bestudeer in het Uitleg de formule voor de inhoud van de kubus.
    1. Bereken de inhoud van een bol waarvan elke ribbe `4` cm is.
    2. Maak elke ribbe twee keer zo groot. Wat gebeurt er met de inhoud?
    3. Bereken hoe groot je de ribben moet nemen om een kubus te krijgen met een inhoud van `500` cm3.

  2. Ook het verband tussen de ribbe `r` en de oppervlakte `A` van een kubus is een machtsverband. De bijbehorende formule is: `A = 6 r^2`.
    1. Is de oppervlakte recht evenredig met de tweede macht van de ribbe, of is de ribbe recht evenredig met de tweede macht van de oppervlakte?
    2. Bereken de oppervlakte van een kubus met ribben van `4` cm.
    3. Hoe groot moet elke ribbe worden om een kubus te krijgen met een 4 maal zo grote oppervlakte?
    4. Leid de formule af die de ribbe uitdrukt in de oppervlakte.

Theorie

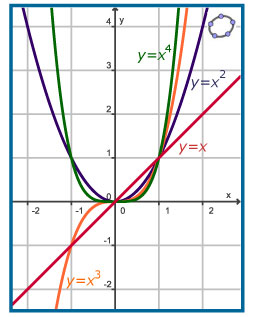
Als `y` recht evenredig met een macht van `x` is, dus `y=c*x^p`, dan spreek je van een machtsfunctie. De constante c is de evenredigheidsconstante.

Je kunt hier voorbeelden van grafieken van machtsfuncties bekijken. Daarbij is `p` steeds een positief getal of 0 en `c=1`.

Vanuit de machtsfunctie y = xp (dus als c = 1) kun je op twee manieren terugrekenen:

Afhankelijk van de waarde van `p` heb je één of twee antwoorden.
Als de evenredigheidsconstante niet de waarde `1` heeft, moet je beginnen met door `c` te delen. Maar daarna pas je ofwel de `p`-de machts wortel toe, ofwel je werkt met de omgekeerde macht.

De rekenregels voor machten (zie ook: "Exponentiële functies") gelden ook nu!

Voor elke x en voor willekeurige reële getallen `a` en `b` gelden de volgende eigenschappen van machten en exponenten:

‡

Voorbeeld 1

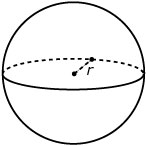
De inhoud van een bol is recht evenredig met de derde macht van de straal: `I = 4/3 pi * r^3`.
Je wilt de straal berekenen van een bol met een inhoud van I = 1000 cm3.

Antwoord

Daarvoor moet je oplossen: `4/3 pi * r^3 = 1000`.
En dus: `r^3 = 238,73...`
Je vindt: `r = root[3](238,73...) ~~ 6,2` cm.

Je kunt ook eerst de formule voor de inhoud van een bol zo omrekenen, dat de straal wordt uitgedrukt in de inhoud. Dat gaat zo:

`4/3 pi * r^3 = I`    delen door `4/3 pi`
`r^3 = 3/(4pi) * I`      terugrekenen vanuit derde macht
`r = (3/(4pi) * I)^(1/3)`.

Je vindt: `r ~~ 0,62 * I^(1/3)`, dus `r` is recht evenredig met `I^(1/3)`.
De evenredigheidsconstante is (ongeveer) 0,62.

‡

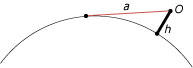
Voorbeeld 2

In een vlak landschap is er een verband tussen hoe ver je kunt kijken en hoe hoog je ogen zich boven het landschap bevinden. Voor de kijkafstand a (in meter) als functie van de hoogte h (in meter) geldt: `a = 3572 * h^(1/2)`.
Omdat `h^(1/2) = sqrt(h)` kun je deze formule ook schrijven als `a = 3572 * sqrt(h)`.

Je kunt bij deze machtsfunctie bij een gegeven waarde van `h` de bijbehorende waarde van `a` berekenen en omgekeerd. Laat dat met voorbeelden zien.

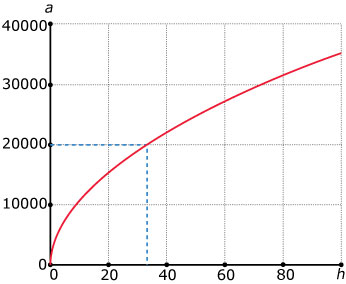
Antwoord

Bijvoorbeeld bij `h=30` m geldt `a = 3572 * 30^(1/2) ~~ 19564` m.

Neem je omgekeerd `a=20` km, ofwel `a=20000` m, dan geldt: `3572 * h^(1/2) = 20000`.
En nu delen door 3572 en vervolgens kwadrateren:
`h = (20000/3572)^2 ~~ 35,4` m.

Beide berekeningen kun je controleren met de grafiek.

‡

Voorbeeld 3

dier    c
muis   9,0
rat   9,1
kat 10,0
konijn   9,8
schaap   8,4
varken   9,0
koe   9,0
paard 10,0
mens 11,2
marmot   9,3
egel   7,5
vleermuis 57,5
vis 10,0
slang 12,5
aap 11,8

De Duitse fysioloog Karl Meeh deed onderzoek naar het verband tussen lichaamsgewicht en huidoppervlakte van verschillende diersoorten. De grootte van de huidoppervlakte is van belang bij het warmteverlies van het dier. Diersoorten met een relatief grote huidoppervlakte in verhouding tot hun inhoud zullen meer energie nodig hebben om op temperatuur te blijven. Ze zullen dan ook in verhouding meer moeten eten. Meeh heeft een formule gevonden die het verband tussen gewicht en huidoppervlakte aangeeft: `H = c * G^(2/3)`.
Hierin is `H` de huidoppervlakte (in dm2) en `G` het gewicht (in kg) van het dier.

Je ziet dat voor dit verschijnsel de huidoppervlakte rechtevenredig is met de 2/3-de macht van het lichaamsgewicht.
De factor `c` is de evenredigheidsconstante en verschilt per diersoort. In de biologie wordt deze evenredigheidsconstante de Meeh-coëfficiënt genoemd. In de tabel is voor een aantal diersoorten de Meeh-coëfficiënt gegeven.

Voor elke diersoort kun je ook een grafiek tekenen. Je ziet dan dat het verband dat Meeh gevonden heeft vooral aangeeft dat hoe zwaarder een dier is, hoe groter het huidoppervlakte is. Dat is logisch, maar je ziet ook dat de huidoppervlakte minder snel toeneemt dan het gewicht: de stijging neemt af. Dat komt door de macht in de fomule. Als je grafieken van twee diersoorten naast elkaar zet, kun je soorten vergelijken. Welke diersoort zal verhoudingsgewijs meer eten nodig hebben?

‡

Hooglander
G H
 430  507
 450  523
 490  553
 500  560
 420  500

Voorbeeld 4

De tabel met Meeh-coëfficiënten (zie Voorbeeld 3) is tot stand gekomen door uit te gaan van de formule die het verband tussen gewicht en huidoppervlakte aangeeft: `H = c * G^(2/3)`.
Hierin is `H` de huidoppervlakte (in dm2) en `G` het gewicht (in kg) van het dier.
`c` is de Meeh-coëfficiënt van een bepaalde diersoort.
In deze tabel zie je vijftal waarden van `G` en `H` van Schotse Hooglanders, een soort koeien. Bepaal de Meeh-coëfficiënt van de Schotse Hooglander.

Antwoord

Breid de tabel uit met een kolom voor `G^(2/3)` en een kolom voor `H/(G^(2/3))`.
Als het goed is vind je in de laatste kolom steeds (ongeveer) hetzelfde getal, namelijk 8,9. Dit is de gevraagde Meeh-coëfficiënt.
Voor de Schotse Hooglanders geldt `H = 8,9 * G^(2/3)`.

‡

Opgaven

  1. In Voorbeeld 1 kom je de formule voor de inhoud van een bol tegen.
    1. `I` is recht evenredig met `r^3`. Wat is de evenredigheidsconstante?
    2. `r` is recht evenredig met `I^(1/3)`. Wat is dan de evenredigheidsconstante?

  2. Bij welke van de volgende formules is `y` recht evenredig met een macht van `x`? Geef in dat geval de evenredigheidsconstante.
    1. `y=2x`
    2. `y=2x^4+5`
    3. `y=5x^4`
    4. `x=5y^4`

  3. Bekijk in Voorbeeld 2 de formule voor de kijkafstand.
    1. Bereken hoe ver je kunt kijken vanaf een toren van `50` m hoog.
    2. Op een eiland wordt een vuurtoren gebouwd. De toren wordt zo hoog gemaakt dat je bij helder weer `25` km ver kunt kijken. Bepaal de hoogte van de toren op de volgende manieren:
      • aflezen uit de grafiek van `a=3572h^(1/2)`;
      • in de formule `a=3572h^(1/2)` de variabele `a` vervangen door `25000`; de vergelijking die je dan krijgt oplossen door hem stapsgewijs te vereenvoudigen;
      • berekenen met de formule `h=(a/3572)^2`.

  4. Bestudeer de Voorbeelden 3 en 4 waarin een verband tussen huidoppervlakte en lichaamsgewicht wordt beschreven. Meeh vond hiervoor de formule: `H=c*G^(2/3)`.
    1. Voor elke diersoort is er een constante `c`. Hoe wordt deze constante genoemd?
    2. Laat door berekening zien dat voor de Schotse Hooglander geldt: `c ~~ 8,9`.
    3. De huid van een bepaalde Schotse Hooglander heeft een oppervlakte van ongeveer `510` dm2. Hoe zwaar was die koe?
    4. Als je deze formule omrekent zodat het lichaamsgewicht uitgedrukt wordt in de huidoppervlakte, wat wordt dan de evenredigheidsconstante?
    5. Als het lichaamsgewicht twee keer zo groot wordt, wordt de huidoppervlakte dan meer of minder dan twee keer zo groot?

  5. Ook voor een massieve bol beschrijft de formule van Meeh het verband tussen de oppervlakte `A` en het gewicht `G`. Ga uit van een massieve ijzeren bol, de soortelijke massa van ijzer is 7,9 g/cm3.
    1. Zoek de formules voor de inhoud van een bol met straal `r` en de oppervlakte van zo'n bol op.
    2. Welke formule geldt voor het gewicht `G` als functie van de straal `r` van de bol? Neem `r` in cm en `G` in gram.
    3. Door de formules voor het gewicht en de oppervlakte van een bol met straal `r` te combineren vind je `A = c * G^(2/3)`. Bepaal de waarde van `c`.

Verwerken

  1. Gegeven is de machtsfunctie `f(x)=120x^5`.
    1. Bereken `f(4)`.
    2. Voor welke waarde van `x` is `f(x)=20000`?
    3. Als de waarde van `x` vier keer zo groot wordt, met hoeveel wordt de bijbehorende functiewaarde dan vermenigvuldigd?

  2. Er is een verband tussen de snelheid s van een auto en de bijbehorende remweg r. De remweg is de afstand die de auto nog aflegt als je zo hard mogelijk remt. Een vuistregel voor dit verband is: `r=(s^2)/100`.
    1. `r` is recht evenredig met een macht van `s`. Wat is de evenredigheidsconstante?
    2. In een weg zit een scherpe bocht waarin je maar 10 meter vooruit kunt kijken. Een eis voor veilig rijden is dat je moet kunnen stoppen binnen de afstand die je kunt overzien. Wat is volgens deze vuistregel de maximumsnelheid in deze bocht?
    3. Geef de formule waarmee de snelheid wordt uitgedrukt in de remweg. Beschrijf in woorden wat voor verband dit is.
    4. Geef commentaar op de volgende uitspraak: "Bij een zicht van 100 meter kun je twee maal zo hard rijden als bij een zicht van 50 meter."

  3. Deze opgave gaat over de inhoud `I` van een kubus met ribben `r` in centimeter.
    1. Bereken de inhoud van een kubus met `r=2`. En ook van een kubus met `r=6`.
    2. De ribbe van de tweede kubus uit a is drie keer zo groot als de ribbe van de eerste. Wat betekent dit voor de inhoud van de kubus?
    3. Een kubus heeft een inhoud van `50` cm. Bereken `r`.
    4. Geef de formule waarmee je de inhoud `I` uitdrukt in `r`.
    5. Geef de formule waarmee je de lengte `r` van de ribbe uitdrukt in inhoud `I`.

  4. Een formule voor de totale oppervlakte `A` van een kubus met ribbe `r` is: `A=6r^2`.
    1. Licht toe hoe je deze formule kunt afleiden.
    2. Bereken de totale oppervlakte van een kubus met ribben van `3` cm en van een kubus met ribben van `6` cm.
    3. Wat gebeurt er met de totale oppervlakte als je de ribben twee keer zo groot maakt?
    4. Van een kubus is de totale oppervlakte `500` cm2. Bereken de lengte van de ribben.
    5. Geef een formule waarmee je de ribbe `r` uitdrukt in de totale oppervlakte `A`.

  5. Ga uit van een massieve ijzeren kubus met straal `r` in cm. De soortelijke massa van ijzer is 7,9 g/cm3.
    1. Stel een formule op voor het gewicht `G` van de kubus als functie van `r`.
    2. Stel een formule op voor de oppervlakte `A` van de kubus als functie van `r`.
    3. Leid een formule af van de vorm `A = c * G^(2/3)`. Bepaal de evenredigheidsconstante `c`.
    4. Bereken het gewicht van zo'n kubus als de totale buitenoppervlakte `150` cm2 is.

Testen

  1. Gegeven is de machtsfunctie `f` met formule `y=5*(3x)^4`.
    1. `y` is recht evenredig met een macht van `x`. Wat is de evenredigheidsconstante?
    2. Voor welke waarden van `x` is `f(x)=120000`?
    3. Als de waarde van `x` vier keer zo groot wordt, met hoeveel wordt de bijbehorende functiewaarde dan vermenigvuldigd?

  2. Het volume van een cilinder kun je berekenen met de formule `V = pi r^2 h`.
    Hierin is `r` de straal van het grondvlak en `h` de hoogte van de cilinder, beide in cm. Je wilt blikken maken die even hoog als breed zijn, dus waarvan `h=2r`.
    1. Welke formule geldt bij deze blikken voor `V` als functie van `r`?
    2. Herschrijf deze formule tot een formule waarin `r` recht evenredig is met een macht van `V`. Bepaal de evenredigheidsconstante.
    3. De oppervlakte van zo'n blik bestaat uit een rechthoek en twee cirkels. Leid een formule af voor de oppervlakte `A` als functie van `r`.
    4. Laat zien dat tussen `A` en `V` een machtsverband bestaat van de vorm `A = c * V^(2/3)`. Bepaal de waarde van `c`.