
Totaalbeeld
Samenvatten
Je hebt nu alle theorie van "Logaritmische functies" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!
Begrippenlijst:
41: logaritme — grondtal
42: definitieformules — eigenschappen van logaritmen
43: logaritmische schaal
44: logaritmische functie
45: logaritmische vergelijkingen en ongelijkheden
Activiteitenlijst:
41: logaritmen gebruiken om exponentiële vergelijkingen op te lossen
42: definitieformules en eigenschappen van logaritmen gebruiken — vergelijkingen met logaritmen oplossen
43: werken met logaritmische schalen — functievoorschrift bepalen van exponentiële functie op enkellogaritmisch papier
44: de karakteristieken van een logaritmische functie bepalen
45: logaritmische vergelijkingen/ongelijkheden oplossen
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Totaalbeeld > Achtergronden
Testen
-
Iemand verwacht dat de komende jaren aandelen 11% per jaar in waarde zullen stijgen.
-
Hoe lang duurt het totdat de waarde van de aandelen 1,5 keer zo groot is geworden?
-
Iemand koopt voor € 2000,= aandelen. Bereken na hoeveel jaar dit bedrag is verdubbeld. Bereken ook na hoeveel jaar het bedrag is verdrievoudigd en na hoeveel jaar het is verzesvoudigd.
Laat zien hoe hiermee de eigenschap g`log(a) + `g`log(b) = `g`log(ab)` toegelicht kan worden.
-
Een doorzichtige kunststof absorbeert per cm 27% van het licht dat er doorheen
valt. Bereken in mm nauwkeurig hoe dik de kunststof moet zijn om 50% van het
licht te absorberen.
-
Los algebraïsch op:
-
1/3`log(x + 2) = -2`
-
2`log(x) = 5 - `2`log(10)`
-
5`log(4x^2) = 2 + `5`log(x)`
-
`10 + 5 * `2`log(x - 5) <= 100`
-
Gegeven zijn de functies `f(x) = log(x + 10) + 4` en `g(x) = log(-x)`.
-
Bepaal van beide functies domein, bereik en de vergelijking van de asymptoot.
-
Bepaal van beide functies algebraÔsch het nulpunt.
-
Los algebraïsch op: `f(x) <= g(x)`.
-
Gegeven is de functie `h(x) = f(x) + g(x)`. Toon aan dat `h(x) = log(-100000x - 10000x^2)`.
-
De luchtdruk `p` in millibar (mbar) hangt af van de hoogte `h` (in km) boven het zeeniveau. Bij benadering geldt:
`h = -15 * log(p/(p_0))`
waarin `p_0` de luchtdruk op zeeniveau voorstelt.
-
Neem aan dat `p_0 = 1010` mbar. Maak de grafiek van `h` als functie van `p`.
-
In een vliegtuig wordt een luchtdruk van 400 mbar gemeten. De luchtdruk op zeeniveau is op dat moment 1010 mbar. Hoe hoog vliegt dat vliegtuig?
-
Verklaar waarom de grafiek van `h` met `p_0 = 930` mbar ontstaat door de grafiek bij a in verticale richting te verschuiven.
-
De bemanning van een vliegtuig gaat uit van 1000 mbar op zeeniveau en berekent dat ze op 3 km hoogte vliegen. De luchtdruk op zeeniveau is echter 1030 mbar. Hoe hoog vliegen ze in werkelijkheid?
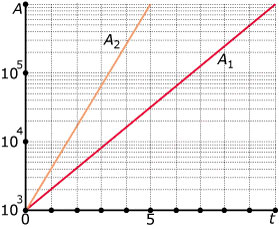 In een laboratorium is onderzocht hoe de toename van het aantal bacteriŽn in 10 g salade afhankelijk is van de temperatuur. In de figuur staan de
resultaten bij een temperatuur van 0 en bij een temperatuur van 4 graden Celcius.
In een laboratorium is onderzocht hoe de toename van het aantal bacteriŽn in 10 g salade afhankelijk is van de temperatuur. In de figuur staan de
resultaten bij een temperatuur van 0 en bij een temperatuur van 4 graden Celcius.
-
Van hoeveel bacteriŽn is bij het onderzoek uitgegaan?
-
Geef zowel voor `A_1` als `A_2`de formule van het aantal bacteriŽn `A` na `t` dagen.
-
Hoeveel keer zoveel bacteriŽn zijn er na tien dagen bij 4°C vergeleken met de situatie bij 0°C?
-
Hoeveel bedraagt de verdubbelingstijd bij een koeling bij 4°C?
Volgens de onderzoekers is er bij de toename van het aantal bacteriŽn als functie
van de temperatuur sprake van toenemende stijging. Voor temperaturen boven
0°C geldt: wordt de temperatuur `a` keer zo hoog, dan wordt de verdubbelingstijd
`a^2` keer zo klein.
-
Geef de verdubbelingstijd van de bacterie bij 6°C. Doe dat ook bij 10°C.
Toepassen
Zuurgraad
In de scheikunde wordt het begrip zuurgraad gebruikt om aan te geven of een bepaalde oplossing meer of minder zuur of basisch is. De zuurgraad wordt voorgesteld door pH en weergegeven op een logaritmische schaal.
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Totaalbeeld > Toepassingen
-
Bij geconcentreerd zwavelzuur is [H+] = 18 Mol/L. Hoeveel bedraagt de zuurgraad?
-
Huishoudammonia (verdunde ammonia) heeft een zuurgraad van 11,5. Hoeveel bedraagt de H+ concentratie in Mol/L?
-
Zure regen heeft een pH-waarde van 4. Hoeveel bedraagt de H+ concentratie van zure regen?
-
Vanaf welke H+ concentratie is de zuurgraad negatief? Is de oplossing dan heel zuur of juist niet?
-
De aanduiding pH-neutraal op cosmetische producten betekent iets anders dan een pH van 7.
Het geeft aan dat het product een pH heeft die overeenkomt met de natuurlijke pH van de huid. De natuurlijk pH van de huid is ongeveer 5,5.
Hoeveel bedraagt de H+ concentratie dan?
C-14 methode
In levende organismen komt behalve het radioactieve koolstof C-14 ook het niet-radioactieve
C-12 voor. Gelukkig is de verhouding van de hoeveelheid C-14 ten
opzichte van C-12 zeer klein. Deze verhouding is constant `1 : 10^(12)`. Wanneer
een organisme sterft verandert de verhouding door radioactief verval van C-14.
Door de verhouding te meten kan de ouderdom van resten organisch materiaal
berekend worden. De halveringstijd van C-14 is 5730 jaar.
-
Een archeoloog vindt een bot waarvan de verhouding C-14 : C-12 gelijk is aan `1 : 10^(13)`. Hoeveel jaar is dat bot ongeveer oud?
-
Bij een Egyptische mummie blijkt de verhouding van C-14 en C-12 ongeveer 0,65 keer de verhouding van C-14 en C-12 in levende organismen te zijn. Benader de ouderdom van deze mummie.
-
In 1947 zijn aan de westzijde van de Dode Zee de Dode-Zeerollen (oudtestamentische handschriften) gevonden.
De verhouding van C-14 en C-12 in de perkamente rollen bleek tussen de 77% en de 81% van die bij levende organismen te zijn.
Vanaf hoeveel jaar voor het begin van de jaartelling tot hoeveel jaar erna zijn de Dode-Zeerollen geschreven?
-
Een 4500 jaar oude kist werd in een hunebed (grafkelder in de provincie Drenthe) aangetroffen.
Hoe groot is de verhouding van de aangetroffen hoeveelheid C-14 en C-12 ongeveer in vergelijking met die van een houten kist uit onze tijd?
De wet van Fechner-Weber
Bekijk eventueel eerst
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Logaritmische schaal > Voorbeeld 3
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Logaritmische schaal > Voorbeeld 3
De wet van Fechner-Weber (naar de negentiende eeuwse Duitse fysiologen
G.Th. Fechner en E.H. Weber) luidt:
Gevoelsindrukken die gelijke verhouding hebben, komen op onze zintuigen over
alsof ze gelijke verschillen hebben.
Onderzoek heeft aangetoond dat een persoon het verschil in geluidsdrukniveau
tussen bijvoorbeeld 2 W/m2 en 20 W/m2 op dezelfde wijze ervaart als het verschil
tussen 20 W/m2 en 200 W/m2.
Toch is het verschil `20 - 2` veel kleiner dan het verschil `200 - 20`. Dat is de reden dat
men bij het toekennen van getalswaarden aan het geluidsdrukniveau in dB de logaritme gebruikt.
-
Toon aan dat daardoor het verschil in dB bij geluidsdrukniveau van 2 W/m2 en van 20 W/m2 gelijk is aan het verschil in dB bij geluidsdrukniveau van 20 W/m2 en 200 W/m2.
-
Laat zien, dat de effectieve geluidsdruk p (in W/m2) een exponentiële functie van het geluidsdrukniveau L (in dB) is.
-
Bij een normaal gesprek is het geluidsdrukniveau 50 dB. Het werken met een drilboor heeft een geluidsdrukniveau van 125 dB.
Iemand zegt dat het geluid van een drilboor `2,5` keer zo hard is als dat van een gewoon gesprek.
Welk bezwaar kun je tegen deze bewering hebben?
Examenopgaven

Aardbevingen
Aardbevingen worden geregistreerd met een seismograaf, die aardbevingsgolven weergeeft in een seismogram.
Verspreid over de aarde staan veel seismografen opgesteld. De uitwijking van een seismograaf hangt af van de afstand van dit instrument tot de plaats aan de oppervlakte van de aarde waar de beving het eerst optreedt. Deze plaats noemt men het epicentrum van de aardbeving. Om aardbevingen met elkaar te kunnen vergelijken gebruikt men seismogrammen die op een afstand van 100 km van het epicentrum zijn gemaakt (standaard seismogrammen). De kracht van een aardbeving wordt meestal uitgedrukt in een getal op de schaal van Richter. Bij deze schaal wordt de logaritme (met grondtal
10) gebruikt van de grootste uitwijking in micrometer die in het seismogram voorkomt.
-
Leg uit, dat de kracht op de schaal van Richter met 1 toeneemt als de maximale uitwijking van de seismograaf 10 keer zo groot wordt.
-
De aardbeving in Nederland van 13 april 1992 had een kracht van 5,5 op de schaal van Richter. De kracht van de aardbeving op 27 februari 2010 in Chili was 8,8.
Bereken de verhouding tussen deze twee grootste uitwijkingen.
Als op een bepaald waarnemingsstation een seismogram gemaakt is en je weet de plaats van het epicentrum, dan kun je met de volgende formule de kracht van de aardbeving berekenen:
`R = log(A/T) + 1,66 * log(D) + 3,30`
Hierin is:
- `R` de kracht van de aardbeving uitgedrukt in een getal op de schaal van Richter;
- `A` de grootste uitwijking in het seismogram in Ķm (1Ķm = 0,001 mm);
- `T` de tijd in seconden van de trilling met de grootste uitwijking;
- `D` de grootte in graden van de hoek tussen de verbindingslijnstukken `ME` en `MW`, waarin `M` het middelpunt van de aarde, `E` het epicentrum van de aardbeving en `W` de plaats van het waarnemingsstation is.
Uit de formule volgt inderdaad dat de kracht op de schaal van Richter met 1 toeneemt als de maximale uitslag van de seismograaf 10 keer zo groot wordt (bij dezelfde `T` en `D`).
-
Toon dit aan.
-
Van de Chileense aardbeving van 2010 werd een seismogram opgenomen. De trillingen gaven daar een maximale uitslag van 1500 Ķm; de trillingstijd `T` bedroeg 20 s.
Na invulling van `D` werd `R = 8,8` gevonden. Neem aan dat de omtrek van de aarde 40000 km is.
Bereken de afstand over de aardbol tussen de plaats waar het seismogram werd opgenomen en het epicentrum in Chili in honderden kilometers nauwkeurig.
-
Ook op diverse andere plaatsen werd in 2010 een seismogram van de Chileense aardbeving opgenomen. Op al die plaatsen berekende men dat de kracht van de aardbeving 8,8 was.
Toon aan dat hieruit volgt dat tussen `A`, `T` en `D` een verband bestaat van de vorm: `D = p * (T/A)^q ` en bereken `p` en `q` in twee decimalen nauwkeurig.
(bron: examen wiskunde B havo 1994, eerste tijdvak, aangepast)
Windsnelheid en hoogte
Op een bepaalde dag is in Vlaardingen op verschillende hoogtes de windsnelheid gemeten. Uit de meetresultaten blijkt dat er bij benadering een lineair verband bestaat tussen de windsnelheid
`W` in m/s en de hoogte h in meter voor hoogten tussen 10 en 80 meter (zie tabel).
De formule `W = a * h + b` geeft dit lineaire verband.
| h | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| W | 1,2 | 1,6 | 2,1 | 2,5 | 3,0 | 3,4 | 3,9 | 4,3 |
-
Bereken `a` en `b` met behulp van de gegevens in de tabel. Rond `a` af op drie decimalen en `b` op twee decimalen.
Onderzoek door weerkundigen naar windsnelheden op verschillende hoogtes en onder verschillende omstandigheden heeft opgeleverd dat het verband tussen windsnelheid en hoogte in het algemeen niet lineair is.
Een betere formule is:
`W = 5,76 * m * log(h/r)`
Hierin is:
- `W` de windsnelheid (in m/s);
- `h` de hoogte in meter waarop de windsnelheid wordt gemeten;
- `m` een constante die afhangt van de wrijving tussen de luchtlagen;
- `r` een constante die afhangt van de ruwheid van het terrein (hoge bomen beÔnvloeden de windsnelheid anders dan grasland)
De formule is geldig tot hoogtes van ongeveer 100 meter.
In de praktijk wordt de windsnelheid op een hoogte van 10 meter gemeten. De waarde van `r` op de meetplek is bekend zodat het getal `m` met behulp van de formule berekend kan worden. Vervolgens kan met de gegeven formule de windsnelheid op andere hoogtes berekend worden.
-
Boven open bouwland met `r = 0,12` wordt de windsnelheid gemeten. Op 10 meter hoogte is deze windsnelheid 6,0 m/s. Bereken in deze situatie de windsnelheid op een hoogte van 60 meter.
-
Boven een bepaald terrein en met `m = 0,45` geldt het volgende: de windsnelheid is op 60 meter hoogte 1,3 keer zo groot als op 20 meter hoogte. Bereken de waarde van `r` van dit terrein.
(bron: examen wiskunde B havo 2006, eerste tijdvak, opgave 4)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Totaalbeeld > Achtergronden  In een laboratorium is onderzocht hoe de toename van het aantal bacteriŽn in 10 g salade afhankelijk is van de temperatuur. In de figuur staan de
resultaten bij een temperatuur van 0 en bij een temperatuur van 4 graden Celcius.
In een laboratorium is onderzocht hoe de toename van het aantal bacteriŽn in 10 g salade afhankelijk is van de temperatuur. In de figuur staan de
resultaten bij een temperatuur van 0 en bij een temperatuur van 4 graden Celcius.
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Totaalbeeld > Toepassingen
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Logaritmische schaal > Voorbeeld 3
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Logaritmische functies > Logaritmische schaal > Voorbeeld 3
