Logaritmische vergelijkingen

Inleiding

Onder andere bij het berekenen van nulpunten van functies ben je al vergelijkingen tegengekomen waarin logaritmen voorkomen. Uit de definitie volgt dat je vanuit een logaritme kunt terugrekenen door een exponentiële functie met hetzelfde grondtal te gebruiken. Hiermee kun je vergelijkingen met logaritmen oplossen. Soms gebruik je er ook de eigenschappen van logaritmen bij.
Bij ongelijkheden moet je ook nog rekening houden met het domein van de logaritme!

Je leert nu:

• systematisch vergelijkingen met logaritmen oplossen;
• ongelijkheden met logaritmische functies oplossen.

Je kunt al:

• werken met logaritmische functies;
• de eigenschappen van logaritmen gebruiken.

Verkennen

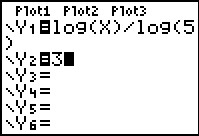
> Los op: ⁵log(x) < 3.

Uitleg

Los op: ⁵log(x) < 3.

Zo'n ongelijkheid los je op m.b.v. grafieken:

• Eerst los je de bijbehorende vergelijking ⁵log(x) = 3 op door aan beide zijden een exponentiële functie met grondtal 5 toe te passen: x = 5³ = 125.
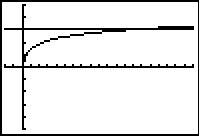
• Vervolgens bekijk je de grafieken van y₁ = ⁵log(x) en y₂ = 3. Daarbij moet je vooral letten op het domein (en de verticale asymptoot) van de logaritme.
• De oplossing wordt: 0 < x < 125.

‡

Opgaven

1. Gegeven is de functie `f(x) = 3 * `²`log(x) + 16`.
   1. Maak de grafiek van `f`.
   2. Bepaal met je grafische rekenmachine voor welke waarde van `x` geldt: `f(x) = 38`.
   3. Bepaal nu ook algebraïsch voor welke waarde van `x` geldt: `f(x) = 38`.
   4. Iemand beweert dat het algebraïsch oplossen van de vergelijking twee voordelen heeft ten opzichte van het grafisch oplossen. Ten eerste kost het nogal wat tijd om het juiste venster in te stellen waaruit je de oplossing kunt aflezen. Ten tweede is de oplossing die je afleest uit de grafiek geen exacte oplossing. Wat vind je van deze bewering?


2. Zie de vorige opgave. Nu moet de ongelijkheid `3 * `²`log(x) + 16 <= 38` worden opgelost.
   1. Bepaal domein, bereik en asymptoot van `f`.
   2. Lees de oplossing van de ongelijkheid af uit de grafiek van `f`.

Theorie

De oplossing van de logaritmische vergelijking ^glog(x) = a vind je door aan beide zijden een exponentiële functie met grondtal g toe te passen.
Uit ^glog(x) = a volgt dan x = g^a.
Hierbij moet g > 0 en g ≠ 1 en a > 0.

De logaritmische ongelijkheid ^glog(x) < a los je op m.b.v. grafieken:

• Eerst los je de bijbehorende vergelijking ^glog(x) = a op.
• Vervolgens bekijk je de grafieken van y₁ = ^glog(x) en y₂ = a. Daarbij moet je vooral letten op het domein (en de verticale asymptoot) van de logaritme.
• De oplossing lees je uit de grafiek af.

Bij ingewikkelder vergelijkingen waarin meerdere logaritmen voorkomen heb je vaak ook nog de eigenschappen van het optellen of aftrekken van logaritmen nodig. Soms moet je zelfs van grondtal wisselen.

‡

Voorbeeld 1

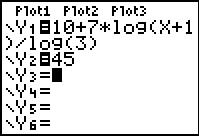
Los op: 10 + 7 · ³log(x + 1) ≤ 45.

Antwoord

Maak meteen de grafieken van y₁ = 10 + 7 · ³log(x + 1) en y₂ = 45 op je GR. Voor de logaritmische functie bedenk je vooraf dat het domein $\langle -\mathrm{1,}\to \rangle$ is, met een verticale asymptoot x = –1. Hiermee en met y₂ = 45 bepaal je de vensterinstellingen.

• 10 + 7 · ³log(x + 1) = 45 geeft: ³log(x + 1) = 5 en dus x + 1 = 3⁵.
  Hiermee vind je: x = 242.
• Nu bekijk je de grafiek en lees je de oplossing af: –1 < x ≤ 242.

Controleer dit allemaal nog even met je GR.

‡

Voorbeeld 2

Los op: ²log(x) + ²log(x + 2) = 3.

Antwoord

Eerst de logaritmen optellen:

²log(x) + ²log(x + 2) = 3 geeft ²log(x(x + 2)) = 3

Dan aan beide zijden een exponentiële functie met grondtal 2 toepassen:

²log(x(x + 2)) = 3 geeft x(x + 2) = 2³

Deze laatste vergelijking kun je oplossen door ontbinden:

x(x + 2) = 2³ geeft x² + 2x – 8 = 0 en dus (x – 2)(x + 4) = 0

Je vindt dus: x = –4  V  x = 2.

Vanwege het domein van een logaritme moet echter x > 0 en x + 2 > 0. Alleen x = 2 voldoet daar aan en dit is daarom de enige oplossing van de gegeven vergelijking.

‡

Voorbeeld 3

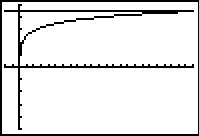
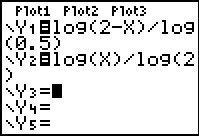
Los algebraïsch op: ^{$\frac{1}{2}$}log(2 – x) ≥ ²log(x).

Antwoord

Maak eerst de grafieken van y₁ = ^{$\frac{1}{2}$}log(2 – x) en y₂ = ²log(x).

• ^{$\frac{1}{2}$}log(2 – x) = ²log(x) los je op door grondtal wisselen, bijvoorbeeld y₁ naar grondtal 2 omzetten:
  ²log(2 – x) / ²log($\frac{1}{2}$) = ²log(x) en dus –²log(2 – x) = ²log(x).
  Dit betekent ²log(2 – x) + ²log(x) = 0 en dus ²log(x(2 – x)) = 0.
  Hieruit volgt: x(2 – x) = 2⁰ = 1 en dus x² – 2x + 1 = 0.
  De oplossing hiervan is x = 1.
• Vervolgens gebruik je de grafieken van y₁ en y₂ om de oplossing af te lezen.

Je vindt dat y₁ altijd groter of gelijk is aan y₂, tenminste binnen beide domeinen van deze functies. De oplossing is daarom: 0 < x < 2.

‡

Opgaven

3. Bekijk in Voorbeeld 1 hoe je een logaritmische ongelijkheid oplost.
   Los op dezelfde manier op: `2 + 3 * `²`log(x - 4) <= 11`.
   


4. Gegeven is de functie `f` met `f(x) = 1 + 4 * `^0,5`log(x + 5)`.
   1. Los algebraïsch op: `f(x) = -3`.
   2. Bepaal domein, bereik en de vergelijking van de asymptoot van `f` en teken de grafiek.
   3. Los op: `f(x) >= -3`.


5. Teken met de grafische rekenmachine de grafieken van de functies `f(x) = `²`log(x)` en `g(x) = `²`log(2 - x)`.
   1. Bepaal van beide functies het domein.
   2. Schrijf van beide functies de vergelijking van de asymptoot op.
   3. Los algebraïsch op: `f(x) = g(x)`.
   4. Los op: `f(x) > g(x)`.


6. In Voorbeeld 2 zie je hoe je bij het oplossen van sommige vergelijkingen de eigenschappen van logaritmen nodig hebt.
   Los algebraïsch op: ⁶`log(x) + `⁶`log(x - 1) = 1`.
   


7. Bekijk Voorbeeld 3.
   Hier moet je om een vergelijking te kunnen oplossen met behulp van de rekenregels van logaritmen van grondtal wisselen.
   1. Los algebraïsch op: ²`log(x) = `^1/2`log(x)`.
   2. Los op: ²`log(x) < `^1/2`log(x)`.


8. Los de volgende vergelijkingen en ongelijkheden algebraïsch op:
   1. ^1/2`log(x) = 4`
   2. ^1/2`log(x) <= 4`
   3. `-5 + 4 * `²`log(x - 2) = 11`
   4. `-5 + 4 * `²`log(x - 2) <= 11`
   5. ³`log(x - 2) = 1 + 5 * `³`log(2)`
   6. `log(2x) - log(x - 1) = 2`

Verwerken

9. Maak de grafiek van de functie `f(x) = 1 - 3 * log(x + 4)`.
   1. Schrijf het domein en het bereik van `f` op.
   2. Los algebraïsch op: `f(x) > 0`.


10. Maak de grafiek van de functie `g(x) = -10 + 2 * `^1/3`log(x - 1)`.
    1. Schrijf het domein en het bereik van `g` op.
    2. Los algebraïsch op: `g(x) >= -14`.


11. Los algebraïsch op:
    1. ³`log(x) = 2 * `³`log(5)`
    2. ^1/3`log(x) = `^1/3`log(5) + `^1/3`log(2)`
    3. `5 - `²`log(x) = 0`
    4. ⁵`log(x) = 3 + 4 * `⁵`log(3)`
    5. ^1/3`log(x) = `^1/3`log(5) + `^1/3`log(2 - x)`
    6. ⁵`log(x) = 3 + 4 * `⁵`log(x)`


12. Gegeven zijn de functies `f(x) = `^1/4`log(x)` en `g(x) = -1 + `⁴`log(x + 3)`.
    1. Bepaal van beide functies het domein, het bereik en de asymptoot.
    2. Los algebraïsch op: `f(x) = g(x)`.
    3. Los op: `f(x) <= g(x)`.
    4. Los op: `f(x) > g(x)`.


13. Los algebraïsch op:
    1. ²`log(x - 3) = `⁴`log(x)`
    2. ²`log(x - 3) > `⁴`log(x)`

Testen

14. Los algebraïsch op:
    1. `1 + 3 * `^1/4`log(x + 6) = -1`
    2. `1 + 3 * `^1/4`log(x + 6) < -1`


15. Los algebraïsch op:
    1. ⁷`log(x - 5) = 0`
    2. `-`^1/4`log(x) = `^1/4`log(5)`
    3. ⁴`log(x) = 0,5 - `⁴`log(3)`
    4. ^1/2`log(x) + `^1/2`log(2x) = 0`


16. Gegeven zijn de functies `f` en `g` met voorschriften `f(x) = `^1/3`log(2x)` en `g(x) = `³`log(3x - 6)`.
    1. Bepaal domein, bereik en de asymptoot van beide functies.
    2. Bereken voor welke `x` geldt `f(x) = -2`.
    3. Los algebraïsch op: `f(x) > 9`.
    4. Bereken voor welke `x` geldt `g(x) = 0`.
    5. Los algebraïsch op: `f(x) = g(x)`.
    6. Los algebraïsch op: `f(x) >= g(x)`.