Logaritmische schalen

Antwoorden bij de opgaven

    1. Nee, tussen 1 en 10 zit een kleinere afstand dan bijvoorbeeld tussen 10 en 100.
    2. `B(5) = 19200` en `B(10) = 614400`.
    3. `t`012345...15
      `log(B)`2,783,083,383,683,984,28...7,29
    4. -
    5. `log(B) = log(600 * 2^t) = log(600) + log(2^t) = log(600) + t * log(2)`.
      De grafiek wordt een rechtelijn door `(0, log(600))` en met richtingscoëfficiënt `log(2)`.
    1. `x`012345...15
      `log(y)`0,300,781,261,732,212,69...7,46
    2. Op de verticale as krijg je

      `log(y)`01234567
      `y``10^0``10^1``10^2``10^3``10^4``10^5``10^6``10^7`
    3. Aflezen: `f(10) ~~ 120000`. GR: `f(10) = 118098`.
    4. `log(y) = log(2 * 3^x) = log(2) + x * log(3)`.
    1. Zie figuur.
    2. Zie figuur.
    3. Zie figuur.
    4. Zie figuur.
    5. `a = 10^(3,5) ~~ 3162,3`
    1. -
    2. `log(N) = log(12000 * 0,8^t) = log(12000) + t * log(0,8)`.
  5. `log(y) = log(b * g^x) = log(b) + x * log(g)`.
    Omgekeerd:
    `log(y) = a * x + b` geeft `y = 10^(ax + b) = 10^(ax) * 10^b = 10^b * (10^a)^x = B * g^x`.
    1. `A(2) ~~ 10^(2,1) ~~ 126` en `A(10) ~~ 10^(3,25) ~~ 1778`
    2. `A(t) = b * g^t` geeft `A(2) ~~ 126 = b * g^2` en `A(10) ~~ 1778 = b * g^(10)`.
      Hieruit volgt: `g^8 ~~ 1778/126 ~~ 14,13` en `g ~~ 14,13^(1//8) ~~ 1,4`.
      En zo vind je dezelfde formule als in Voorbeeld 2.
    3. `A(0) = b`
    1. `(0,10^0) = (0,1)`
    2. Lees af de punten `(-4,1000)` en `(5; 0,01)`.
      Dus `N(-4) = b * g^(-4) = 1000` en `N(5) = b * g^(5) = 0,01`.
      Hieruit volgt: `g^9 = 0,01/1000 = 0,00001` zodat `g = 0,00001^(1//9) ~~ 0,28`.
      Je vindt na invullen: `b ~~ 5,99`. Dus `N(t) ~~ 6 * 0,28^t`.
    3. `N(t) = 1` geeft `0,28^t ~~ 0,167` en dus `t ~~ `0,28`log(0,167) ~~ 1,40`. Het snijpunt wordt ongeveer `(1,40; 1)`.
    4. `N(t) > 0` voor elke `t`.
    1. `35 = 20 * log(p/(0,00002))` geeft `p = 0,00002 * 10^(35//20) ~~ 0,0011` Pa.
    2. `55 = 20 * log(p/(0,00002))` geeft `p = 0,00002 * 10^(55//20) ~~ 0,0112` Pa.
      `95 = 20 * log(p/(0,00002))` geeft `p = 0,00002 * 10^(95//20) ~~ 1,1247` Pa.
      Dat is samen `1,1359` Pa en dat is `20 * log((1,1359)/(0,00002)) ~~ 95,1` dB, dus nauwelijks meer dan de drilboor alleen.
    3. `110 = 20 * log(p/(0,00002))` geeft `p = 0,00002 * 10^(110//20) ~~ 6,3246` Pa.
      `130 = 20 * log(p/(0,00002))` geeft `p = 0,00002 * 10^(130//20) ~~ 63,2456` Pa.
      Dus 10 keer zo groot.
    1. `A(t) = 80000 * 1,06^t`
    2. -
    3. Schatting: ongeveer 190000, GR geeft `A(15) ~~ 191725`.
    1. `t`0123456
      `log(N)`1,701,922,152,372,602,833,05
    2. Ja, je krijgt ongeveer een rechte lijn door `(0; 1,70)` en `(4; 2,60))`. Omdat de grafiek van `log(N(t))` bij benadering een rechte lijn is, is `N(t)` bij benadering een exponentiële functie.
    3. `log(N) ~~ 1,70 + 0,22t`
    4. `N(t) ~~ 10^(1,70 + 0,22t) = 10^(1,70) * (10^(0,22))^t ~~ 50 * 1,66^t`
    1. Voor `V(t) = b * g^t` geldt: `V(0) = 2 = b * g^0` en `V(5) = 6 = b * g^5`.
      Dit levert op: `b = 2` en `g^5 = 6/2 = 3`, zodat `g ~~ 1,25`. Een passende formule is `V(t) ~~ 2 * 1,25^t`.
    2. `V(t) = 10` geeft `1,25^t = 5` en dus `t = `1,25`log(5) ~~ 7,21`.
    3. `V(t) = 1` geeft `1,25^t = 0,5` en dus `t = `1,25`log(0,5) ~~ -3,11`.
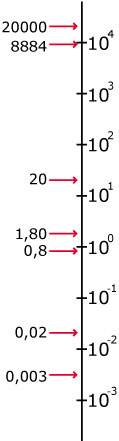
    1. Bij de maatbolletjes staan machten van 10.
    2. `log(m) ~~ 1,1` en `log(P) ~~ 2,4`.
    3. `log(P) = a * log(m) + b` door `(1,1; 2,4)` en `(2,9; 2,0)`.
      Dit geeft `a = (-0,4)/(1,8) ~~ -0,22` en `b ~~ 2,64`, dus `log(P) ~~ -0,22 * log(m) + 2,64`.
    4. `P ~~ 10^(-0,22 * log(m) + 2,64) = (10^log(m))^(-0,22) * 10^(2,64) ~~ 440 * m^(-0,22)`.


    1. `10^(1,1) ~~ 12,59`
    2. Zie figuur.
    3. Zie figuur.
    4. Zie figuur.
    1. -
    2. De punten liggen ongeveer op een rechte lijn door `(0, 40)` en `(4, 200)`.
    3. Punten liggen ongeveer op een rechte lijn, dus exponentiële groei.
    4. `N(t) = 40 * 1,495^t` met `t` in weken.