Bijzondere functies

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Bijzondere functies > Inleiding

Probeer de drie vragen in Verkennen te beantwoorden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Bijzondere functies > Uitleg

Bekijk de eerste pagina van de Uitleg. Twee auto’s rijden met een constante snelheid over dezelfde weg. Auto 1 gaat van `A` naar `B` met een constante snelheid van 90 km/h en auto 2 van `B` naar `A` met een constante snelheid van 120 km/h.
1. In de Uitleg wordt de afstand van beide auto’s tot `A` bekeken. Bekijk die afstand nu vanuit `B`. Schrijf de twee bijpassende formules op.
2. Onderzoek door berekening of beide auto’s elkaar nu op hetzelfde tijdstip tegenkomen.
3. Op pagina 2 van de Uitleg vind je een passende verschilgrafiek met afstanden t.o.v. `A`. Maak nu zelf een grafiek van hun onderlinge afstand met de afstanden t.o.v. `B`.
4. Voor welke twee waarden van `t` bedraagt die onderlinge afstand 20 km?

Twee fietsers komen elkaar op `t = 0` tegen. Beiden fietsen met een snelheid van 18 km/h. Hun onderlinge afstand `a` in m hangt af van de tijd in s.
1. Welk voorschrift heeft `a` als functie van `t`?
2. Bereken de tijdstippen waarop de onderlinge afstand 90 m is.

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Functies en grafieken > Bijzondere functies > Theorie

Bekijk pagina 1 van de Theorie. Elke lineaire functie f heeft een functievoorschrift van de vorm `f(x) = ax + b`. In de applet kun je de waarden van de parameters `a` en `b` aanpassen.
1. Welke betekenis heeft de parameter `a` voor de grafiek van `f`?
2. Welke betekenis heeft de parameter `b` voor de grafiek van `f`?
3. Welke waarden voor `a` en `b` moet je instellen om als grafiek een rechte lijn door `A(1,2)` en `B(5,3)` te krijgen?
4. Hoe kun je het bijbehorende functievoorschrift afleiden uit de coördinaten van `A` en `B`?

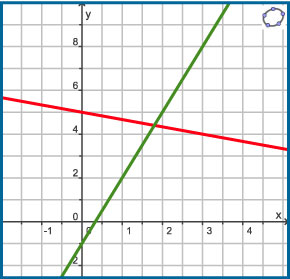Bekijk in Voorbeeld 1 hoe je het voorschrift opstelt van een lineaire functie als twee punten van de grafiek zijn gegeven. Je ziet hier twee grafieken van lineaire functies. Stel voor elk van deze functies een passend voorschrift op en bereken algebraïsch het snijpunt van beide lijnen.

Bekijk pagina 2 van de Theorie. De absoluutfunctie is ook op je grafische rekenmachine te vinden.
1. Breng de grafiek van `f(x) = |x|` met je grafische rekenmachine goed in beeld.
2. Welk knikpunt heeft de grafiek van `f`?
3. Los op: `|x| = 6`.
4. Waarom is de vergelijking `|x| = -2` niet oplosbaar?

Bekijk de grafieken van de functie `y_1 = |x| - 2` en `y_2 = |x - 3|`.
1. Schrijf bij elk van deze functies het voorschrift in gesplitste vorm, dus zonder absoluutstrepen.
2. Bereken algebraïsch het snijpunt van beide grafieken.
3. Los bij beide functies de vergelijking `y = 4` op.

Bekijk Voorbeeld 2. Het gaat daarin om de "afstand" `a(x) = |y_1 - y_2|` tussen de grafieken van `y1 = x^2` en `y_2 = 6 - x`.
1. Teken de grafiek van `a(x)` op je grafische rekenmachine.
2. Waarom staat "afstand" tussen aanhalingstekens?
3. Voor welke `x` is de "afstand" tussen beide grafieken gelijk aan 4?

Bekijk weer pagina 2 van de Theorie en bekijk daarna Voorbeeld 3. De entierfunctie is ook op je grafische rekenmachine te vinden.
1. Wat is er niet goed aan de grafiek die de GR maakt van y = int(x)?
2. Los op: int(x) = 2.

Gegeven is de functie `f` met `f(x)` = int(`2x`) – 1.
1. Bereken `f(2,43)` en `f(-pi)`.
2. Schrijf het domein en het bereik van `f` op.
3. Los op: `f(x) = 4`.

Stel een voorschrift op van de lineaire functie waarvan de grafiek gaat door de punten `P(2,80)` en `Q(8,140)`.

Een echtpaar wil vanaf het station met de taxi naar huis. Ze kunnen kiezen tussen een treintaxi en een gewone taxi. De treintaxi kost € 3,00 per persoon. De gewone taxi rekent € 2,25 per rit en daarboven op nog € 0,75 per minuut.
1. Bij de gewone taxi is de ritprijs (`R`) afhankelijk van het aantal minuten (`a`) dat je er in zit. Stel het bijbehorende functievoorschrift `R(a)` op.
2. Bij welke reistijd is het voordeliger om een treintaxi te nemen?
3. Taxi’s rijden in de stad gemiddeld 30 km/h. Wat raad je dit echtpaar aan als ze 5 km van het station wonen?

Twee cilindervormige kaarsen worden tegelijkertijd aangestoken. Ze branden gelijkmatig op. Een uur na het aansteken heeft kaars I een lengte van 75 cm en is kaars II nog 71 cm lang. 3, 5 uur na het aansteken worden beide kaarsen opnieuw gemeten: kaars I is dan 62,5 cm en kaars II is dan nog 61 cm lang.
1. Stel voor elk van deze kaarsen een formule op voor de lengte `L` in cm als functie van de brandtijd `t` in uren.
2. Hoeveel uur na het aansteken zijn beide kaarsen even lang?
3. Hoeveel uur na het aansteken verschillen ze 1 cm in lengte?

Gegeven is het functievoorschrift `y(x) = ||x - 2| - 2|`.
1. Verklaar waarom de grafiek van deze functie de vorm van de letter W heeft.
2. Bereken algebraïsch de nulpunten van deze functie.
3. Los op: `y = 1`.
4. Verzin zelf een functievoorschrift waarmee je een letter M (een omgekeerde W) in beeld krijgt die symmetrisch ligt ten opzichte van de `y`-as.

Gegeven is de functie `f` met `f(x) = 4x|x - 1|`.
1. In welk punt heeft de grafiek van deze functie een knik?
2. Schrijf het functievoorschrift in gesplitste vorm, zonder absoluutstrepen.
3. Los op: `y < 0,5`.

De grafiek van de functie `f` met `f(x) = |ax + b|` gaat door de punten `(0,3)`, `(1,1)` en `(4,5)`. Bepaal de juiste waarden van de parameters `a` en `b`.

Bekijk de grafieken van `y_1` = int(`2x + 1`) en `y_2 = x +` int(`x`) op je grafische rekenmachine met domein `[-4,4]`.
1. Schrijf van elk van beide functies het bereik op.
2. Hebben deze grafieken gemeenschappelijke punten? Licht je antwoord toe.
3. Los op: `y_2 = 2x`.

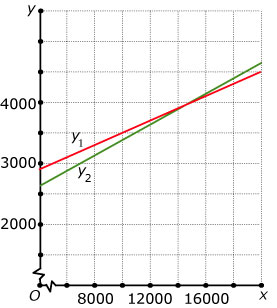
Je ziet de grafieken van de jaarlijkse kosten van twee verschillende auto’s. Auto A was duurder in de aanschaf en heeft mede daarom hogere vaste kosten per jaar, maar is per gereden kilometer iets goedkoper.
1. Stel voor beide auto’s een passende formule op voor de jaarlijkse kosten als functie van het aantal gereden kilometers.
2. Bereken vanaf welk aantal gereden kilometers per jaar het voordeliger is om auto A aan te schaffen.

De grafiek van een lineaire functie gaat door de punten `A(-24,42)` en `B(30,16)`. Stel een passend functievoorschrift op.

Gegeven is de functie `f` met `f(x) = 0,5x + |x - 1| + |1 + 2x|`.
1. Waarom kent de grafiek van `f` twee knikpunten?
2. Schrijf het functievoorschrift zonder absoluutstrepen in gesplitste vorm.
3. Wat is het bereik van deze functie?
4. Los op: `f(x) >= 4`.