
Totaalbeeld
Samenvatten
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Exponentiële en logaritmische functies > Totaalbeeld > Samenvatten
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Exponentiële en logaritmische functies > Totaalbeeld > Samenvatten
Je hebt nu het onderwerp Exponentiële en logaritmische functies doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!
Begrippenlijst:
- het getal e — de natuurlijke logaritme — afgeleide van f(x) = ex
- differentieerregels — de kettingregel
- afgeleiden van exponentële functies
- afgeleiden van logaritmische functies
- enkellogaritmisch en dubbellogaritmisch grafiekenpapier — geremde exponentiële groei
- primitieven van exponentiële en logaritmische functies
Activiteitenlijst:
- werken met het getal e en de natuurlijke logaritme
- de kettingregel gebruiken
- exponentiële functies differentiëren
- logaritmische functies differentiëren
- verschillende groeimodellen herkennen — werken met enkel- en dubbellogaritmisch grafiekenpapier
- exponentiële en logaritmische functies primitiveren — deze primitieven gebruiken om integralen exact te berekenen.
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Exponentiële en logaritmische functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Exponentiële en logaritmische functies > Totaalbeeld > Achtergronden
Testen
Opgaven
-
Gegeven is de functie `f(x) = -2 ln(x - 4) + 2`.
- Bepaal de vergelijking van de asymptoot van de grafiek van `f` en schrijf het domein van `f` op.
- Bereken de snijpunten van de grafiek van `f` met de assen. Geef benaderingen in drie decimalen nauwkeurig.
- Stel een vergelijking op van de raaklijn aan de grafiek van `f` in het snijpunt van de grafiek met de `x`-as.
- Los algebraïsch in drie decimalen nauwkeurig op: `-10 < f (x) < 10`.
-
Gegeven is de functie `y = text(e)^(- 1/2 x^2)`.
- Bepaal algebraïsch het bereik van deze functie.
- Bereken de waarden van `x` waarin het hellingsgetal van deze functie een grootste of een kleinste waarde aanneemt.
- Schets de grafieken van `y` en van `(text(d)y)/(text(d)x)`.
-
Gegeven zijn de functies `f(x) = 2^x + 2^(-x)` en `g(x) = 2^x + 4`.
- Los algebraïsch op: `f(x) < g(x)`.
- Bereken met behulp van primitiveren de oppervlakte van het gebied dat wordt ingesloten door beide grafieken en de `y`-as.
Op de grafiek van `f` ligt punt `A` met `x`-waarde `p`. Op de grafiek van `g` ligt punt `B` met `x`-waarde `p`.
- Voor welke waarden van `p` is de lengte van lijnstuk `AB` gelijk aan `8`?
- Los op: `f(x) + g(x) = -2`.
-
Belangrijk nieuws verspreidt zich razendsnel. Het aantal leerlingen `N` dat op een
zeker tijdstip `t` van een belangrijk feit op de hoogte is, wordt gegeven door de
formule
`N(t) = 1200(1 - text(e)^(-0,31t))`
Hierin is `t` in uren en is `t = 0` om 09:00 uur.
- Op grond van deze formule kun je concluderen dat het aantal leerlingen dat van een belangrijk feit op de hoogte is uiteindelijk ongeveer constant wordt.
Leg uit waarom.
- Geef de vergelijking van de asymptoot.
- Bereken algebraïsch op welk tijdstip er 550 leerlingen van het feit gehoord hebben. Rond in het antwoord af op minuten.
- Voor de snelheid `v` waarmee het nieuws zich verspreidt geldt: `v(t) = (text(d)N)/(text(d)t)`. Hoe ziet de formule voor de snelheid van de nieuwsverspreiding er uit?
Kun je op grond van deze formule dezelfde conclusies als bij a trekken?
- Toon algebraïsch aan dat de grafiek van `N` stijgend is.
- Met welke snelheid verspreidt het nieuws zich om kwart voor 11? Geef het antwoord in gehelen per minuut.
- Op welk tijdstip is de snelheid van de nieuwsverspreiding de helft van die om 09:00 uur? Geef dit tijdstip in minuten nauwkeurig.
-
Gegeven zijn de functies `f(x) = log(4 - x^2)` en `g(x) = log(3x)`.
- Bepaal van beide functies het domein en het bereik.
- Los algebraïsch op: `f(x) >= g(x)`.
- De grafieken snijden elkaar in punt `S`. `l` is de raaklijn aan de grafiek van `f` in `S`, `m` is de raaklijn aan de grafiek van `g` in `S`.
Bereken de hoek waaronder beide raaklijnen elkaar snijden.
-
Gegeven is de functie `f` door `f(x) = (4 ln(x))/(1 + ln^2(x))`.
- Bepaal het domein van `f`.
- Bereken algebraïsch de karakteristieken van de grafiek van `f`.
- Los algebraïsch op: `f(x) <= 1`.
De raaklijn aan de grafiek van `f` in het punt waarvoor geldt `x = text(e)^2`, snijdt de `x`-as in punt `A` en de `y`-as in punt `B`.
- Bereken de lengte van lijnstuk `AB`.
-
Gegeven is voor elke waarde van `p != 0` de functie `f_p(x) = (x^2 - px)e^(-px)`.
- Voor welke waarden van `k` heeft de vergelijking `f_1(x) * f_(-1)(x) = k` geen oplossingen?
- De grafiek van `f_p` heeft een buigpunt dat op de `x`-as ligt. Bereken `p`.
- Onderzoek voor welke waarden van `p` de functie `f_p` een maximum heeft. Druk voor die waarden van `p` dat maximum uit in `p`.
Toepassen
Radioactiviteit
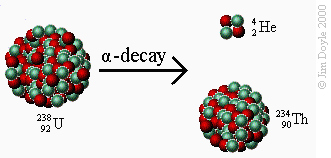 Radioactiviteit is een eigenschap van bepaalde instabiele zeer zware metalen. Bekende voorbeelden zijn radium en uranium. Het gaat daarbij om stoffen waarvan de atoomkern straling (in de vorm van bepaalde deeltjes) uitzendt. Soms is deze straling schadelijk voor leven.
Radioactiviteit is een eigenschap van bepaalde instabiele zeer zware metalen. Bekende voorbeelden zijn radium en uranium. Het gaat daarbij om stoffen waarvan de atoomkern straling (in de vorm van bepaalde deeltjes) uitzendt. Soms is deze straling schadelijk voor leven.
Een voorbeeld is U-238, een isotoop van uranium die door het uitstoten van ?-deeltjes (deeltjes die bestaan uit twee protonen en twee neutronen) wordt omgezet in thorium, Th-234. Uranium is een metaal dat in de natuur vookomt, ruim 98% daarvan is U-238.
De halfwaardetijd is de tijd die nodig is om de helft van de oorspronkelijke hoeveelheid om te zetten in thorium. De halfwaardetijd is voor elke radioactieve stof een bepaald constant getal. De halfwaardetijd van U-238 is ongeveer `4,468 * 10^9` jaar.
- Omdat de halfwaardetijd voor een radioactieve stof een constant getal is, is de hoeveelheid `H` van die stof als functie van de tijd `t` te beschrijven met een formule van de vorm
`H(t) = H(0) * text(e)^(kt)`.
Leg uit waarom dat zo is.
- Op `t = 0` heb je 1 kg U-238. Stel nu een formule op voor `H(t)`.
Neem `t` in miljarden jaren. `k` heet de desintegratieconstante.
- Waarom is de desintegratieconstante niet afhankelijk van de hoeveelheid U-238 waarmee je begint?
Bij onderzoek in het menselijk lichaam gebruiken artsen de stof jodium-131. Die stof is radioactief en daardoor kunnen deeltjes ervan in het menselijk lichaam van buitenaf worden gevolgd. De halveringstijd (of halfwaardetijd) van jodium-131 is 8,06 dagen.
- Bereken de desintegratieconstante van jodium-131.
- Toon aan dat in dit model de vervalsnelheid recht evenredig is met de hoeveelheid radioactieve stof. Hoe groot is de bijbehorende evenredigheidsconstante?
- Na hoeveel dagen is er nog 10% van de beginhoeveelheid over?
- Na hoeveel dagen is de vervalsnelheid (de radioactiviteit) verminderd tot 10% van de beginsnelheid?
- Als een meetnauwkeurigheid in mg van twee decimalen maximaal haalbaar is, na hoeveel dagen is de ingespoten 5 mg jodium-131 dan niet meer meetbaar? Is de stof ooit volledig verdwenen?
Vissen in de Grevelingen
De Grevelingen (thans het Grevelingenmeer) is een voormalige zeearm van de Noordzee, gelegen tussen de eilanden Goeree-Overflakkee en Schouwen-Duiveland, op de grens van de provincies Zuid-Holland en Zeeland. In het kader van de Deltawerken werd de Grevelingen door de Grevelingendam (1965) en de Brouwersdam (1971) van zee afgesloten.
Het Grevelingenmeer is het grootste zoutwatermeer van West-Europa, en is vooral van belang voor de watersport en recreatie. Het zoutgehalte van het Grevelingenmeer wordt op peil gehouden door de Brouwerssluis, een doorlaatsluis in de Brouwersdam, waarmee zeewater ingelaten wordt.
Een gebied met een oppervlakte van 13.872 ha is aangemerkt als beschermd Natura 2000-gebied.
 In 1985 werd voor enkele vissoorten het verloop van hun populatiegrootte in modellen beschreven. Omdat enkele vissoorten zoals de schol zich in het afgesloten Grevelingenmeer niet meer konden voortplanten moest de mens een handje helpen. De larven van de schol zwemmen recht op na hun geboorte en zien er dan ook uit als andere vissen. Na ongeveer 6 weken ondergaan ze een gedaanteverwisseling, waarbij een van hun ogen naar de andere kant groeit en ze zich tot platvis ontwikkelen en een jonge schol worden. Voor de schol werden er twee modellen ontworpen:
In 1985 werd voor enkele vissoorten het verloop van hun populatiegrootte in modellen beschreven. Omdat enkele vissoorten zoals de schol zich in het afgesloten Grevelingenmeer niet meer konden voortplanten moest de mens een handje helpen. De larven van de schol zwemmen recht op na hun geboorte en zien er dan ook uit als andere vissen. Na ongeveer 6 weken ondergaan ze een gedaanteverwisseling, waarbij een van hun ogen naar de andere kant groeit en ze zich tot platvis ontwikkelen en een jonge schol worden. Voor de schol werden er twee modellen ontworpen:
- Model A: Er worden jaarlijks 5 miljoen larven en 200.000 schollen ouder dan 1 jaar uitgezet in het Grevelingenmeer.
- Model B: Er worden jaarlijks 2 miljoen larven en 100.000 schollen ouder dan 1 jaar uitgezet in het Grevelingenmeer.
Voor beide modellen geldt dat de sterfte onder jonge schollen (jonger dan 1 jaar) 90% per jaar is en onder schollen ouder dan 1 jaar 33% per jaar. Alle larven worden jonge schollen.
- Maak op grond van model A een tabel van het aantal schollen ouder dan 1 jaar gedurende de eerste 10 jaren na 1985. Neem aan dat er in 1985 nog 500.000 schollen ouder dan 1 jaar in het Grevelingenmeer zaten.
Ga er van uit dat in 1985 het aantal schollen van 1 jaar of ouder 300.000 bedroeg.
- Teken een grafiek van het aantal schollen `S` ouder dan 1 jaar in de loop van de jaren.
- Voor `S` geldt een groeimodel van de vorm `S(t) = G - a * e^(bt)`. Welke waarde voor `G` schat je op grond van de grafiek bij b)? Bereken nu ook de waarden van `a` en `b`.
- Er is in dit model nog geen rekening gehouden met bevissing. De visserijmortaliteit is 23% per jaar. Wat betekent dit?
- Pas je model aan en onderzoek wat dit betekent voor het aantal schollen op den duur.
CV-installatie
Het verloop van de temperatuur van een huis is veel complexer dan dat van een afkoelende kop koffie of een opwarmend blikje cola. Denk bijvoorbeeld aan zonne-instraling, cv, tocht, etc. Toch spelen ook aan de basis hiervan exponentiële functies een rol.
Je kijkt eerst naar een ruimte in de vorm van een balk, en verwaarloost tocht en zonnestraling. Hoe reageert de temperatuur van zo’n huis op het aan- en uitzetten van de cv?
Ga uit van de situatie dat de buitentemperatuur constant gelijk is aan 10°C, en de binnentemperatuur gelijk aan 20°C. Als de cv niet aanstaat, dan heb je ongeveer de situatie van de afkoelende kop koffie: de snelheid waarmee de temparatuur `T` in huis daalt is recht evenredig met het temperatuursverschil met de buitentemperatuur.
- Voor een bepaald huis is de waarde van de evenredigheidsconstante `c` gelijk aan `-0,0018` (eenheid: min–1). Hoe lang duurt het voor het binnen is afgekoeld tot 15 graden Celsius?
En hoelang duurt het voor de temperatuur een halve graad is gezakt?
- Hoeveel graden neemt de temperatuur in het begin af per minuut, en hoeveel na een uur?
Bij 19,5 graden zet je de cv aan. Dit zorgt voor een temperatuurstijging. Hoe groot zal deze worden? Dat hangt af van veel factoren, waarvan de belangrijkste zijn: de grootte van de cv-ketel, en de grootte van het warmteverlies naar de omgeving. Bij een grotere cv-ketel zal de eindtemperatuur ook hoger zijn. Stel dat de eindtemperatuur Tc voor dit huis 35 graden is (je zult lang daarvoor de cv natuurlijk uitschakelen, maar het gaat nu om de "evenwichtssituatie" die zal ontstaan als je de cv steeds aan laat staan). Hoe zal het temperatuurverloop zijn?
Er geldt: `(text(d)T)/(text(d)t) = c * (T - T_c)` (waarbij `c` de zelfde evenredigheidsconstante is als in de situatie zonder cv!), en `T_c` de eindtemperatuur is in het geval dat de cv blijft aanstaan.
- Ga na dat de temperatuur volgens de formule inderdaad stijgt.
- Hoelang duurt het voor het weer 20 graden Celsius is?
Je wilt de temperatuur nu zo dicht mogelijk bij die 20 graden houden. Met een besturingssysteem zet je de cv nu steeds aan- en uit als je hier een halve graad van afzit. Je kunt dan de temperatuurkromme tekenen. Er ontstaat een soort zaagtand.
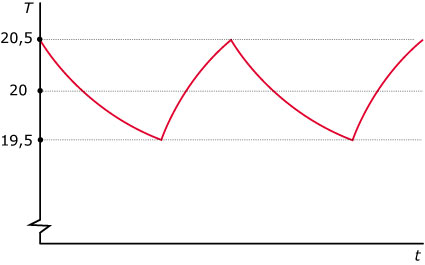
- Hoe lang duurt het voor de cv weer afslaat? Hoe lang duurt het vervolgens voor hij opnieuw aanspringt? Wat is dus de periode van de temperatuurregeling? Welk deel van de tijd brandt de cv?
- Stel je voor dat je de cv-ketel sneller kunt aansturen, door de cv te schakelen bij een kwart graad afwijking van de gewenste temperatuur. Hoelang wordt de periode dan?
Welk deel van de tijd brandt de cv? Licht de antwoorden toe.
Als het buiten kouder wordt, kan de cv de ruimte minder goed verwarmen. De “evenwichtstemperatuur” zakt dan ook: de cv kan de ruimte tot maximaal 25 graden boven de buitentemperatuur verwarmen.
- 's Avonds koelt het buiten af tot 3 graden Celsius. Bereken nu in beide gevallen de periode en het percentage dat de cv brandt. De waarde van `c` blijft gelijk.
Verouderende populaties
Van een zekere populatie neemt met een toenemende leeftijd `x` van het individu
het aantal individuen van die leeftijd meestal af. Die afname wordt door demografen uitgedrukt in het sterftecijfer `m` (van "mortality"), dat is het deel van het aantal individuen van een bepaalde leeftijd dat er jaarlijks sterft. Bij een constant sterftecijfer neemt het aantal individuen van een bepaalde leeftijd `S(x)` (van "survivors") exponentieel af.
- Verklaar waarom dat zo is.
 Bij verouderende populaties blijft het sterftecijfer niet constant, maar wordt het bij hogere leeftijden steeds groter. In dat geval geldt de zogenaamde Gompertzvergelijking:
Bij verouderende populaties blijft het sterftecijfer niet constant, maar wordt het bij hogere leeftijden steeds groter. In dat geval geldt de zogenaamde Gompertzvergelijking:
`m(x) = M * text(e)^(G * x)`
waarin `M` het sterftecijfer van volgroeide individuen voorstelt en `x` de leeftijd is
van een individu. `G` heet de Gompertz-constante. Deze Gompertz-constante is een maat voor de verouderingssnelheid.
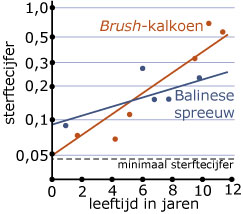
Hier zie je de grafieken van `m(x)` voor de Australische Brush-kalkoen en de Balinese spreeuw. Van Australische Brush-kalkoenen is `M = 0,05` en `G = 0,21`.
- Ga na hoe deze getallen zijn terug te vinden in de grafieken van het sterftecijfer.
- Stel voor deze soort een Gompertz-vergelijking voor het sterftecijfer op en ga na of hij past bij de getekende grafiek.
- Als een populatie Brush-kalkoenen 100 volgroeide 0-jarige individuen kent, hoeveel 10-jarige individuen zou die populatie dan moeten hebben?
- Schat nu zelf met behulp van de grafiek de waarden van `M` en `G` die gelden voor de Balinese spreeuw. Stel ook voor deze soort de Gompertz-vergelijking op.
Een andere maat voor de veroudering van een populatie is de verdubbelingstijd van het sterftecijfer, de `SCVT`.
- Toon aan dat `SCVT = (ln(2))/G`.
- Bereken ook de `SCVT` voor zowel de Brush-kalkoen als de Balinese spreeuw.
- `S(x)` stelt het aantal volwassen individuen van een populatie met de leeftijd `x` voor. Teken grafieken van `S(x)` voor een populatie Australische Brush-kalkoenen en voor een populatie Balinese spreeuwen.
Ga bij beide populaties uit van 100 volgroeide 0-jarige individuen. Vergelijk beide grafieken en de verouderingsprocessen van beide populaties.
Examenopgaven
Aardbevingen
Aardbevingen worden geregistreerd met een seismograaf, die aardbevingsgolven weergeeft in een seismogram.
Verspreid over de aarde staan veel seismografen opgesteld. De uitwijking van een seismograaf hangt af van de afstand van dit instrument tot de plaats aan de oppervlakte van de aarde waar de beving het eerst optreedt. Deze plaats noemt men het epicentrum van de aardbeving. Om aardbevingen met elkaar te kunnen vergelijken gebruikt men seismogrammen die op een afstand van 100 km van het epicentrum zijn gemaakt (standaard seismogrammen).
De kracht van een aardbeving wordt meestal uitgedrukt in een getal op de schaal van Richter. Bij deze schaal wordt de logaritme (met grondtal 10) gebruikt van de grootste uitwijking in micrometer die in het seismogram voorkomt.
- Leg uit, dat de kracht op de schaal van Richter met 1 toeneemt als de maximale uitwijking van de seismograaf 10 keer zo groot wordt.
De aardbeving in Nederland van 13 april 1992 had een kracht van 5,5 op de schaal van Richter. De kracht van de aardbeving op 27 februari 2010 in Chili was 8,8.
- Bereken de verhouding tussen deze twee grootste uitwijkingen.
Als op een bepaald waarnemingsstation een seismogram gemaakt is en je weet de plaats van het epicentrum, dan kun je met de volgende formule de kracht van de aardbeving berekenen:
`R = log(A/T) + 1,66 * log(D) + 3,30`
Hierin is:
- `R` de kracht van de aardbeving uitgedrukt in een getal op de schaal van Richter;
- `A` de grootste uitwijking in het seismogram in μm (1 μm = 0,001 mm);
- `T` de tijd in seconden van de trilling met de grootste uitwijking;
- `D` de grootte in graden van de hoek tussen de verbindingslijnstukken `ME` en `MW`, waarin `M` het middelpunt van de aarde, `E` het epicentrum van de aardbeving en `W` de plaats van het waarnemingsstation is.
Uit de formule volgt inderdaad dat de kracht op de schaal van Richter met 1 toeneemt als de maximale uitslag van de seismograaf 10 keer zo groot wordt (bij dezelfde `T` en `D`).
- Toon dit aan.
Van de Chileense aardbeving van 2010 werd een seismogram opgenomen. De trillingen gaven daar een maximale uitslag van 1500 μm; de trillingstijd `T` bedroeg 20 s.
Na invulling van `D` werd `R = 8,8` gevonden. Neem aan dat de omtrek van de aarde 40000 km is.
- Bereken de afstand over de aardbol tussen de plaats waar het seismogram werd opgenomen en het epicentrum in Chili in honderden kilometers nauwkeurig.
Ook op diverse andere plaatsen werd in 2010 een seismogram van de Chileense aardbeving opgenomen. Op al die plaatsen berekende men dat de kracht van de aardbeving 8,8 was.
- Toon aan dat hieruit volgt dat tussen `A`, `T` en `D` een verband bestaat van de vorm: `D = p * (T/A)^q` en bereken `p` en `q` in twee decimalen nauwkeurig.
(bron: examen wiskunde B havo 1994, eerste tijdvak, aangepast)
-
Als een patiënt een dosis van een medicijn toegediend krijgt, zal de concentratie van dit medicijn in het bloed eerst toenemen en daarna afnemen.
Van een bepaald medicijn wordt de concentratie `C` (in mg/cm3) in het bloed gegeven door de formule:
`C(t) = 0,12 * t * text(e)^(-0,5t)`
Hierbij is `t` het aantal uren na het toedienen van één dosis van het medicijn.
Van dit medicijn is bekend dat het werkzaam is zolang `C` groter is dan 0,035 mg/cm3.
De tijd dat het medicijn werkzaam is bij 1 keer toedienen is minder dan 6 uur.
- Bereken in minuten nauwkeurig hoe lang het medicijn in dit geval werkzaam is.
Er geldt: `C'(t) = 0,12(1 - 0,5t)text(e)^(-0,5t)`
- Toon dit aan.
Er is een tijdstip waarop de concentratie het sterkst afneemt.
- Bereken dit tijdstip.
Het medicijn wordt in gelijke doses toegediend met tussenpozen van 6 uur.
Omdat 6 uur na de eerste keer toedienen van het medicijn een tweede dosis wordt toegediend, geldt vanaf `t = 6` tot `t = 12` de volgende formule voor de concentratie
`C^(text(*))` (in mg/cm3) van het medicijn in het bloed:
`C^(text(*))(t) = C(t) + C(t - 6)`
Bij elke nieuwe dosis verandert de formule voor de concentratie van het medicijn in het bloed.
In elke periode van 6 uur heeft de concentratie van het medicijn in het bloed een maximale waarde. De maximale waarde wordt in elke volgende periode van 6 uur iets groter.
Het medicijn kan schadelijke gevolgen hebben als de concentratie boven de 0,11 mg/cm3 komt.
- Onderzoek of dit het geval is binnen 24 uur na het begin van het toedienen van het medicijn.
(bron: examen wiskunde B vwo 2007, tweede tijdvak)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Exponentiële en logaritmische functies > Totaalbeeld > Samenvatten
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Exponentiële en logaritmische functies > Totaalbeeld > Samenvatten![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Exponentiële en logaritmische functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Exponentiële en logaritmische functies > Totaalbeeld > Achtergronden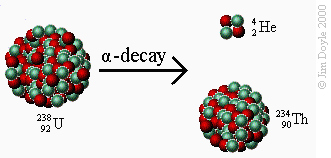 Radioactiviteit is een eigenschap van bepaalde instabiele zeer zware metalen. Bekende voorbeelden zijn radium en uranium. Het gaat daarbij om stoffen waarvan de atoomkern straling (in de vorm van bepaalde deeltjes) uitzendt. Soms is deze straling schadelijk voor leven.
Radioactiviteit is een eigenschap van bepaalde instabiele zeer zware metalen. Bekende voorbeelden zijn radium en uranium. Het gaat daarbij om stoffen waarvan de atoomkern straling (in de vorm van bepaalde deeltjes) uitzendt. Soms is deze straling schadelijk voor leven.
 In 1985 werd voor enkele vissoorten het verloop van hun populatiegrootte in modellen beschreven. Omdat enkele vissoorten zoals de schol zich in het afgesloten Grevelingenmeer niet meer konden voortplanten moest de mens een handje helpen. De larven van de schol zwemmen recht op na hun geboorte en zien er dan ook uit als andere vissen. Na ongeveer 6 weken ondergaan ze een gedaanteverwisseling, waarbij een van hun ogen naar de andere kant groeit en ze zich tot platvis ontwikkelen en een jonge schol worden. Voor de schol werden er twee modellen ontworpen:
In 1985 werd voor enkele vissoorten het verloop van hun populatiegrootte in modellen beschreven. Omdat enkele vissoorten zoals de schol zich in het afgesloten Grevelingenmeer niet meer konden voortplanten moest de mens een handje helpen. De larven van de schol zwemmen recht op na hun geboorte en zien er dan ook uit als andere vissen. Na ongeveer 6 weken ondergaan ze een gedaanteverwisseling, waarbij een van hun ogen naar de andere kant groeit en ze zich tot platvis ontwikkelen en een jonge schol worden. Voor de schol werden er twee modellen ontworpen:

 Bij verouderende populaties blijft het sterftecijfer niet constant, maar wordt het bij hogere leeftijden steeds groter. In dat geval geldt de zogenaamde Gompertzvergelijking:
Bij verouderende populaties blijft het sterftecijfer niet constant, maar wordt het bij hogere leeftijden steeds groter. In dat geval geldt de zogenaamde Gompertzvergelijking: