Integralen

Inleiding

Nu je exponentiële en logaritmische functies kunt differentiëren, kun je ook primitieven van dergelijke functies afleiden. Die heb je nodig om oppervlaktes onder vlakdelen, inhouden van omwentelingslichamen, lengtes van krommen, en dergelijke exact te kunnen berekenen als bij het beschrijven ervan exponentiële en/of logaritmische functies worden gebruikt.

Je leert nu:

• de primitieven van exponentiële en logaritmische functies kennen;
• integralen berekenen waarin exponentiële en/of logaritmische functies voorkomen.

Je kunt al:

• werken met exponentiële en logaritmische functies;
• differentiëren met alle basisregels;
• de afgeleiden van exponentiële en logaritmische functies opstellen.

Verkennen

Uit de afgeleiden van de exponentiële en de logaritmische functies kun je een hele lijst met primitieven samenstellen.

> Welke primitieven kun je zelf verzinnen?
> Licht toe dat uit f(x) = $\frac{1}{x}$ volgt: F(x) = ln(|x|) + c.
(Waarom die absoluutstrepen???)

Uitleg

Uit de afgeleiden van de exponentiële en de logaritmische functies kun je een hele lijst met primitieven samenstellen.

• Als f(x) = e^x, dan is f'(x) = e^x.
  Dus: als f(x) = e^x, dan is F(x) = e^x + c.
• Als f(x) = g^x, dan is f'(x) = g^x · ln(g).
  Dus: als f(x) = g^x, dan is F(x) = $\frac{1}{\ln (g)}\cdot g^x$ + c.
• Als f(x) = ln(x), dan is f'(x) = $\frac{1}{x}$ (met x > 0).
  Dus: als f(x) = $\frac{1}{x}$ (met x > 0), dan is F(x) = ln(x) + c.
  Is echter x < 0, dan is f(x) = –$\frac{1}{-x}$.
  De primitieve is dan: F(x) = –ln(–x) · –1  + c = ln(–x) + c.
  Dit kun je samenvatten tot: als f(x) = $\frac{1}{x}$, dan is F(x) = ln(|x|) + c.
  Nu worden de haakjes van de ln-functie vaak weggelaten!

Moeilijker is het vinden van de primitieve van f(x) = ln(x).
Maar je kunt wel bewijzen dat F(x) = x ln(x) – x + c als afgeleide heeft: F'(x) = ln(x).
En dan heb je toch een geschikte primitieve gevonden.
Vervolgens is f(x) = ^glog(x) ook niet moeilijk meer te primitiveren...

‡

Opgaven

1. Bekijk de Uitleg. Er worden primitieven bepaald van exponentiële en logaritmische functies.
   1. Als `f(x) = g^x` dan is `F(x) = 1/(ln(g)) * g^x + c`. Laat zien dat dit klopt door `F` te differentiëren.
   2. Leid de primitieve van `g(x) = text(e)^x` af uit die van `f(x) = g^x`.
   Neem nu de functie `h(x) = 2 + 0,5text(e)^(2x)`.
   3. Bereken `int_0^2 h(x) text(d)x`.
   4. Wat heb je met de integraal uit c uitgerekend?


2. In de Uitleg wordt verteld dat `F(x) = ln|x| + c` de primitieve is van `f(x) = 1/x`.
   1. Laat met behulp van differentiëren zien dat dit juist is.
   2. Welke primitieve heeft `g(x) = 4/(x + 2)`?
   3. Welke primitieve heeft `h(x) = 4/(2x + 4)`?


3. In de Uitleg wordt verteld dat `F(x) = xln(x) - x + c` de primitieve is van `f(x) = ln(x)`.
   1. Laat met behulp van differentiëren zien dat dit juist is.
   2. Welke primitieve heeft `f(x) = ^(g) log(x)`?

Theorie

Om te kunnen werken met integralen waarin exponentiële en logaritmische functies voorkomen heb je een lijst nodig met primitieven van exponentiële en logaritmische functies.

• Als f(x) = e^x, dan is F(x) = e^x + c.
• Als f(x) = g^x, dan is F(x) = $\frac{1}{\ln (g)}\cdot g^x$ + c.
• Als f(x) = $\frac{1}{x}$, dan is F(x) = ln|x| + c.
  Je ziet dat de haakjes van de ln-functie zijn weggelaten!
• Als f(x) = ln(x), dan is F(x) = x ln(x) – x + c.

Functies waarin de hierboven genoemde functies voorkomen kun je nu af en toe ook primitiveren. Maar omdat het aantal methoden dat je leert voor het primitiveren beperkt is, moet je bij het berekenen van een integraal nog regelmatig terugvallen op je grafische rekenmachine voor een benadering.

‡

Voorbeeld 1

Hier zie je hoe enkele functies worden geprimitiveerd:

• f(x) = 5^x geeft F(x) = $\frac{1}{\ln 5}$ · 5^x + c

• f(x) = 5^2x geeft F(x) = $\frac{1}{\ln 5}$ · 5^2x · $\frac{1}{2}$ + c = $\frac{1}{2\ln (5)}$ · 5^x + c

• f(x) = ⁵log(x) = $\frac{\ln (x)}{\ln (5)}=\frac{1}{\ln (5)}\cdot \ln (x)$ geeft F(x) = $\frac{1}{\ln (5)}$(x ln(x) – x) + c

• f(x) = e^–0,5x geeft F(x) = e^–0,5x · $\frac{1}{\mathrm{0,5}}$ + c = 2 e^–0,5x + c

• f(x) = (e^x + $\frac{1}{{\text{e}}^x}$)² = e^2x + 2 + e^–2x geeft:
  F(x) = 0,5 e^2x + 2x – 0,5 e^–2x + c

‡

Voorbeeld 2

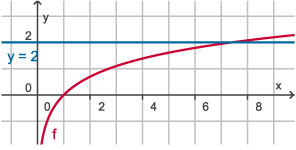
Het vlakdeel V wordt ingesloten door de grafiek van f(x) = ln(x), de lijn y = 2 en de beide coördinaatassen.
Bereken de exacte oppervlakte van V.

Antwoord

De grafiek van f snijdt de x-as in (1,0).
De grafiek van f snijdt de lijn y = 2 in (e²,2).

Opp(V) = ${\displaystyle \underset{0}{\overset{{\text{e}}^2}{\int }}2\text{d}x}-{\displaystyle \underset{1}{\overset{{\text{e}}^2}{\int }}\ln (x)\text{d}x}$ = ${[2x]}_0^{{\text{e}}^2}-{[x\ln (x)-x]}_1^{{\text{e}}^2}$ = e² – 1.

‡

Voorbeeld 3

Het vlakdeel V uit voorbeeld 2 wordt gewenteld om de y-as. Bereken de exacte inhoud van het omwentelingslichaam dat zo ontstaat.

Antwoord

Omdat voor de grafiek van f geldt y = ln(x), wordt x = e^y.

Inh(V) = ${\displaystyle \underset{0}{\overset{2}{\int }}\text{π}}{({\text{e}}^y)}^2\text{d}y=\text{π}{\displaystyle \underset{0}{\overset{2}{\int }}{\text{e}}^{2y}\text{d}y}=\text{π}{[\frac{1}{2}{\text{e}}^{2y}]}_0^2$ = π(e⁴ – 1).

‡

Voorbeeld 4

Bereken de omtrek van het vlakdeel V uit voorbeeld 2 in twee decimalen nauwkeurig.

Antwoord

De grafiek van f snijdt de x-as in (1,0).
De grafiek van f snijdt de lijn y = 2 in (e²,2).

De gevraagde omtrek bestaat uit de lengtes van drie lijnstukken en de lengte van de grafiek van f tussen x = 1 en x = e² samen.
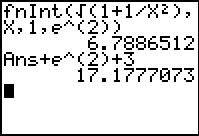
Dus: Omtrek(V) = 1 + 2 + e² + ${\displaystyle \underset{1}{\overset{{\text{e}}^2}{\int }}\sqrt{1+{(f\text{'}(x))}^2}\text{d}x}$ = 3 + e² + ${\displaystyle \underset{1}{\overset{{\text{e}}^2}{\int }}\sqrt{1+\frac{1}{x^2}}\text{d}x}$ ≈ 17,18.

‡

Opgaven

4. Primitiveer de volgende functies, zie Voorbeeld 1.
   1. `f(x) = text(e)^(x + 1)`
   2. `f(x) = 5 + 3 * 2^(4x)`
   3. `f(x) = 2x + 1/x`
   4. `f(x) = 3/(2x + 1)`
   5. `f(x) = ln(3x)`
   6. `f(x) = 2/(text(e)^(4x))`


5. Bepaal de volgende integralen met behulp van primitiveren.
   1. `int_ 0^2 3/(3x + 4) text(d)x`
   2. `int_0^4 0,5^(2x - 1) text(d)x`
   3. `int_1^2 (x^4 + 5x^2)/(x^3) text(d)x`
   4. `int_(0,25)^(text(e)) ln(4x) text(d)x`


6. Gegeven is de functie `f(x) = text(e)^x`. Het vlakdeel `V` wordt ingesloten door de grafiek van `f`, de lijn `x = 2` en de twee coördinaatassen.
   1. Bereken de oppervlakte van `V`. Bekijk eventueel eerst Voorbeeld 2.
   2. Het vlakdeel `V` wordt om de `x`-as gewenteld. Bereken exact de inhoud van het omwentelingslichaam dat daardoor ontstaat.
   3. Het vlakdeel `V` wordt om de `y`-as gewenteld, zie ook Voorbeeld 3. Bereken met behulp van de grafische rekenmachine de inhoud van het omwentelingslichaam dat daardoor ontstaat in twee decimalen nauwkeurig.
   4. Bereken de omtrek van vlakdeel `V` in twee decimalen nauwkeurig, zie ook Voorbeeld 4.


7. Gegeven is de functie `f` door `f(x) = x + 1/x`.
   `V` is het vlakdeel ingesloten door de grafiek van `f` en de lijn `y = 2 1/2`.
   1. Bereken met behulp van primitiveren de oppervlakte van `V`.
   2. Het vlakdeel `V` wordt gewenteld om de `x`-as. Bereken met behulp van primitiveren de inhoud van het omwentelingslichaam dat daardoor ontstaat.
   3. Bereken met behulp van de grafische rekenmachine de omtrek van `V`.

Verwerken

8. Bereken de volgende integralen exact en controleer je antwoord met de grafische rekenmachine.
   1. `int_0^1 1/(2x + 1) text(d)x`
   2. `int_0^1 x^(2 text(e)) - text(e)^(2x) text(d)x`
   3. `int_(0,25)^1 ln(4x) text(d)x`
   4. `int_1^4 (x + 4)/(2x) text(d)x`
   5. `int_0^1 2 + 5 * 10^(0,5x) text(d)x`
   6. `int_1^2 log(3x) text(d)x`


9. Bepaal de primitieve functie `F(x)` als bekend is dat:
   1. `f(x) = -0,25text(e)^(-1/2x) + text(e)` en `F(0) = 1`
   2. `f(x) = 1 - log(x)` en `F(1) = 0`


10. Gegeven is de functie `f` met `f(x) = (x^2 - 4)/(2x)`.
    `V` is het vlakdeel ingesloten door de grafiek van `f`, de `x`-as en de lijn `x = 4`.
    1. Bereken exact de oppervlakte van `V`.
    2. Bereken de omtrek van `V` in twee decimalen nauwkeurig.
    3. `V` wordt gewenteld om de `x`-as. Bereken de exacte inhoud van het omwentelingslichaam dat daardoor ontstaat.


11. Gegeven is de functie `f(x) = (2text(e)^x)/(text(e)^x + 1)`.
    1. Laat zien dat `f'(x) = (2text(e)^x)/((text(e)^x + 1)^2)`.
    2. Bepaal de oppervlakte van het gebied tussen de `x`-as en de functie `g(x) = (2text(e)^x)/((text(e)^x + 1)^2)` op het interval `[0,2]`.
    Voor `a > 0` is `G_a` het gebied ingesloten door de grafiek van `f` en de `x`-as op `[-a,a]`.
    3. Bereken de exacte waarde van `a` waarvoor de oppervlakte van `G_a` gelijk is aan `1`.


12. Gegeven zijn de functies `f_p` door `f_p(x) = pxtext(e)^(-x^2)`.
    `V_p` is het vlakdeel ingesloten door de grafiek van `f`, de `x`-as en de lijn `x = 2`.
    1. Toon aan dat `F(x) = -0,5ptext(e)^(-x^2) + c` de primitieve is van `f`.
    2. Bereken de oppervlakte van `V_1`.
    3. Voor welke `p` is de oppervlakte van `V_p` gelijk aan 10?

Testen

13. Bereken de volgende integralen met behulp van primitiveren.
    1. `int_1^2 (2/x + text(e)^x) text(d)x`
    2. `int_0^1 (text(e)^x + text(e)^(2x))/(text(e)^x) text(d)x`
    3. `int_1^2 4/(2x + 3) text(d)x`
    4. `int_1^2 (1 - 3/x)^2 text(d)x`
    5. `int_2^4 ln(x - 1) text(d)x`
    6. `int_0^2 2^(3x) text(d)x`


14. Gegeven is `f(x) = text(e)^(x/3) - 2x + 5`.
    Bereken de oppervlakte van het gebied ingesloten door de grafiek van `f`, de `y`-as, de lijn `y = 5 - 2x`, de `x`-as en de lijn `x = 6`.
    


15. Gegeven is de functie `f` door `f(x) = text(e)^(x) + text(e)^(-x)`.
    `V` is het vlakdeel ingesloten door de grafiek van `f` en de lijnen `y = 4`.
    1. Bereken algebraïsch de extremen van `f`.
    2. Los op: `f(x) < 4`.
    3. Bereken exact de oppervlakte van `V`.
    4. Bereken exact de inhoud van het lichaam dat ontstaat door `V` om de `x`-as te wentelen.