Logaritmische functies

Inleiding

Je kunt functies met een voorschrift van de vorm f(x) = g^x differentiëren. En met behulp daarvan leer je nu logaritmische functies differentiëren. Daarbij maak je gebruik van de definitieformules van logaritmen.

Je leert nu:

• de afgeleide van een logaritmische functie bepalen;
• van dergelijke functies de hellingen, de extremen en de buigpunten berekenen.

Je kunt al:

• exponenten en logaritmen gebruiken;
• differentiëren met alle basisregels en dit toepassen bij het berekenen van hellingen, extremen en buigpunten;
• de afgeleide van f(x) = g^x bepalen.

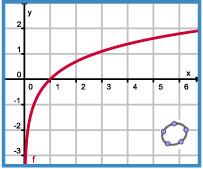
Verkennen

Je ziet hier de grafiek van `f(x) = ln(x)`. Je wilt de bijbehorende afgeleide bepalen.

> Breng de afgeleide van `f(x) = ln(x)` (bij benadering) in beeld.
> Waarom heeft de grafiek van deze afgeleide bij x = 0 een verticale asymptoot?
> De grafiek van de afgeleide heeft ook een horizontale asymptoot. Welke?
> Kun je een functievoorschrift voor de afgeleide verzinnen?

Uitleg

De afgeleide van `f(x) = ln(x)` kun je vinden door te gebruiken dat `text(e)^(ln(x)) = x`.
Bekijk de functie `g(x) = text(e)^(ln(x))`.
Omdat `g(x) = text(e)^(ln(x)) = text(e)^u` met `u = ln(x)` is `g'(x) = text(e)^u * u'(x)`.
Omdat `g(x) = x` geldt ook `g'(x) = 1`.
Dus is `text(e)^u * u'(x) = 1`, dus `u'(x) = 1/(text(e)^u) = 1/(text(e)^(ln(x)) = 1/x`.
Conclusie: uit `u(x) = ln(x)` volgt `u'(x) = 1/x'.

• De afgeleide van `f(x) = ln(x)` is `f'(x) = 1/x`.

Nu je de afgeleide van `f(x) = ln(x)` hebt gevonden, kun je die van `f(x) = `^g`log(x)` er uit afleiden door te gebruiken dat ^g`log(x) = (ln(x))/(ln(g))` .

‡

Opgaven

1. In de Uitleg wordt de afgeleide van `f(x) = ln(x)` bepaald.
   Differentieer de volgende functies en bereken de richtingscoëfficiënt van de raaklijn aan de grafiek van `f` voor `x = 10`.
   1. `f(x) = ln(5x)`
   2. `f(x) = 3ln(4 - x)`
   3. `f(x) = ln(1/x)`


2. Bepaal nu zelf de afgeleide van `f(x) = `²`log(x)`. Gebruik daarbij ²`log(x) = (ln(x))/(ln(2))`.
   


3. Bepaal de afgeleide van `f(x) = `^g`log(x)`. (Neem aan dat `g > 0` en `g != 1`.)
   

Theorie

De afgeleide van de natuurlijke logaritmische functie f(x) = ln(x) is f'(x) = $\frac{1}{x}$.

De afgeleide van de g-logaritme f(x) = ^glog(x) is hieruit af te leiden door te gebruiken dat ^glog(x) = $\frac{\ln (x)}{\ln (g)}$.
Je vindt:

Als f(x) = ^glog(x), dan is f'(x) = $\frac{1}{\ln (g)\cdot x}$.

Verder kun je nu allerlei functies waarin vormen als ln(x) en/of ^glog(x) voorkomen differentiëren met de differentieerregels. Daarmee kun je van functies die ingewikkelder zijn dan zuiver logaritmische functies ook de karakteristieken bepalen.

‡

Voorbeeld 1

Hier zie je voorbeelden van het differentiëren van functies waarin logaritmen voorkomen:

• f(x) = ⁵log(x) geeft f'(x) = $\frac{1}{\ln (5)\cdot x}$

• f(x) = ⁵log(2x) geeft f'(x) = $\frac{1}{\ln (5)\cdot 2x}$ · 2 = $\frac{1}{\ln (5)\cdot x}$

• f(x) = x · ⁵log(2x) geeft f'(x) = 1 · ⁵log(2x) + x · $\frac{1}{\ln (5)\cdot x}$ = ⁵log(2x) + $\frac{1}{\ln (5)}$

• N(t) = 6000 – 2000 · log(–0,5t) geeft N'(t) = –2000 · $\frac{1}{\ln (10)\cdot \mathrm{0,5}t}$ · 0,5 = $\frac{-2000}{\ln (10)\cdot t}$

• K(q) = 100 · ln(q^–1) + 12 · ln(2q) = –100 ln(q) + 12 ln(2q) geeft:
  K'(q) = $\frac{-100}{q}+\frac{12}{2q}\cdot 2=\frac{-88}{q}$

• f(x) = $\frac{3{\ln }^2(x)}{x}$ geeft: f'(x) = $\frac{6\ln (x)\cdot \frac{1}{x}\cdot x-3{\ln }^2(x)\cdot 1}{x^2}=\frac{6\ln (x)-3{\ln }^2(x)}{x^2}$

‡

Voorbeeld 2

De luchtdruk p (in hectopascal hPa) hangt af van de hoogte h in km boven het aardoppervlak. In een luchtballon is de luchtdruk gemakkelijk te meten en wordt daaruit de hoogte berekend met de formule:
h = –6,5 log$\left(\frac{p}{p_0}\right)$
Hierin is p₀ de luchtdruk op zeeniveau. Neem aan dat p₀ = 1000 hPa.
Bereken nu de hoogte en de snelheid waarmee h(p) verandert als p = 920 hPa wordt gemeten.

Antwoord

Als p₀ = 1000 hPa dan is h = –6,5 log(0,001p).

Als p = 920 hPa dan is h ≈ 0,235 km.
Je zit dan 235 m boven zeeniveau.

h'(p) = –6,5 · $\frac{1}{ln(10)}$ · $\frac{1}{\mathrm{0,001}p}$ · 0,001 = $\frac{-\mathrm{2,823}}{p}$.

Als p = 920 hPa dan is h' ≈ –0,003.
Bij een toename van de luchtdruk daalt de hoogte met ongeveer 3 m/hPa.

‡

Voorbeeld 3

Gegeven is de functie f met f(x) = x ln²(x).

1. Bereken algebraïsch de extremen van f.
2. Bereken de coördinaten van de punten op de grafiek van f waarin de raaklijn evenwijdig is aan de lijn met vergelijking y = 3x.

Antwoord

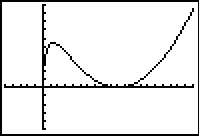
Om de grafiek te kunnen tekenen stel je vast dat het domein $\langle \mathrm{0,}\to \rangle$ en het nulpunt (1,0) is.

De afgeleide van f is: f'(x) = ln²(x) + 2 ln(x).

De extremen vind je uit ln²(x) + 2 ln(x) = 0.
Dit geeft ln(x) · (ln(x) + 2) = 0, dus ln(x) = 0  V  ln(x) = –2 en dus x = 1  V  x = e^–2.
Dus zijn de extremen min.f(1) = 0 en max.f(e^–2) = 4e^–2.

In de tweede vraag is het gegeven te vertalen in f'(x) = 3.
Dit geeft: ln²(x) + 2 ln(x) = 3 en dus ln²(x) + 2 ln(x) – 3 = 0.
Dit levert op: ln(x) = 3  V  ln(x) = –1 en dus x = e³  V  x = e^–1.
De gevraagde punten zijn (e³,9e³) en (e^–1,e^–1)

‡

Opgaven

4. Bepaal van de volgende functies de afgeleide en los op: `f'(x) = 10`. Bekijk eventueel eerst Voorbeeld 1.
   1. `f(x) = ln(4x)`
   2. `f(x) = `³`log(x)`
   3. `f(x) = 5 log(x)`
   4. `f(x) = 50 ln(2x) + 100`
   5. `f(x) = `²`log(50 + x^2)`
   6. `f(x) = 2/(ln(3x))`


5. Bekijk Voorbeeld 2. Neem nu aan dat `p_0 = 1020`.
   1. Bepaal voor deze waarde van `p_0` de afgeleide van `h(p)`.
   2. Bereken `h` en de veranderingssnelheid van `h` als er 900 hPa wordt gemeten in de ballon.
   3. Hoe kun je aan de afgeleide van `h` zien dat de grafiek van `h` voor elke waarde van `p` dalend is?


6. Gegeven zijn de functies `f(x) = ln(2x + 4)` en `g(x) = ln(-x)`.
   1. Bepaal van beide functies het domein. Bij welke instellingen van het venster van de grafische rekenmachine krijg je van beide functies de karakteristieken goed in beeld?
   2. Los algebraïsch op: `f(x) <= g(x)`.
   3. De grafieken van `f` en `g` snijden elkaar in punt `S`. Hoe groot is de hoek die de raaklijnen aan de grafieken van `f` en `g` in `S` met elkaar maken?


7. In Voorbeeld 3 wordt de functie `f` met `f(x) = x ln^2(x)` bekeken.
   1. Bepaal zelf de afgeleide van `f` en bereken de extremen van `f`.
   2. Bereken het buigpunt van de grafiek van `f` en stel een vergelijking op van de raaklijn aan die grafiek in dit buigpunt.


8. Gegeven is de familie van functies `f_n` met het voorschrift `f_n(x) = x^n ln(x)` met `n` een positief geheel getal.
   1. Waarom is er geen functie van deze familie waarvan de top op de lijn `y = 2` ligt?
   2. Bereken de hoek waaronder de grafiek van elke functie `f_n` de `x`-as snijdt.
   3. Druk de buigpunten van de grafieken van `f_n` uit in `n`. Hoeveel buigpunten heeft elke grafiek?
   4. Op de grafiek van `f_2` ligt een punt `P` waarin de raaklijn aan die grafiek door de oorsprong van het assenstelsel gaat. Bereken de coördinaten van `P`.

Verwerken

9. Bepaal `f'(x)` en stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 1`.
   1. `f(x) = `²`log(2 - x)`
   2. `f(x) = ln(x^2 + 4x)`
   3. `f(x) = x ln(2x)`
   4. `f(x) = (ln(x))/x`
   5. `f(x) = ^(x + 1) log(text(e))`


10. Gegeven is de functie `f` met voorschrift `f(x) = 2/x + ln(2x)`.
    1. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 1`.
    2. Bereken algebraïsch het minimum van `f`.
    3. Voor welke `x` heeft de raaklijn aan de grafiek van `f` een richtingscoëfficiënt van `-1`?


11. Bekijk de grafieken van de functies `f(x) = ^2 log(6 - x)` en `g(x) = - ^2 log(x)` met domein `[0, 6]`.
    1. Bereken in twee decimalen nauwkeurig de coördinaten van de snijpunten van de grafieken van `f` en `g`.
    Op de grafieken van `f` en `g` liggen punten `A` en `B` beide met `x`-waarde `k`. Neem aan dat `1 < k < 4`.
    2. Toon aan dat de lengte van `AB` dan maximaal `2 * ^2 log(3)` is.
    Op de grafieken van `f` en `g` liggen punten `C` en `D` beide met `y`-waarde `p`.
    3. Toon aan dat voor de lengte `l` van `CD` geldt: `l(p) = 6 - 2^p - 1/(2^p)`.
    4. Bereken de maximale lengte van `CD`.


12. Gegeven is de functie `f(x) = x(ln(x) - 1)`.
    1. Bereken algebraïsch de karakteristieken van de grafiek van `f`.
    2. Teken een nauwkeurige grafiek van `f` voor `0 <= x <= 3`. Laat daarin duidelijk zien hoe de grafiek van `f` er in de buurt van `(0, 0)` uitziet.
    3. Er ligt een punt op de grafiek van `f` waarin de raaklijn aan die grafiek door het punt `(0, 1)` gaat. Bereken de coördinaten van dat punt.


13. Gegeven zijn de functies `f_p` door `f_p(x) = x^2 - ln(px)` met `p > 0`.
    1. Toon aan dat de grafieken van alle functies `f_p` door verschuiving in de `y`-richting uit elkaar kunnen ontstaan.
    2. De grafiek van `f_p` heeft een extreme waarde van `1`. Bereken `p`.
    3. Toon aan dat de grafieken van `f_p` geen buigpunt hebben.



14. Geluidsdrukniveau

    Voor het geluidsdrukniveau `L` geldt de formule:

    `L = 10 * log(I/(I_0))`

    Hierin is l de geluidsintensiteit in W/m² (Watt per m²). De grootheid `L` wordt veel gebruikt om geluidshinder te meten. Hij wordt uitgedrukt in decibel (dB).
    1. Bij de gehoorgrens (`L = 0`) is de geluidsintensiteit `10^(-12)` W/m². Bij de pijngrens is de geluidsintensiteit 10 W/m². Bereken het geluidsdrukniveau bij de pijngrens.
    Op een bepaalde afstand produceren twee personenauto’s elk een geluidsdrukniveau van 80 dB. Nu kun je hun gezamenlijke geluidsdrukniveau niet krijgen door beide afzonderlijke geluidsdrukniveaus op te tellen. Dat kan echter wel met hun afzonderlijke geluidsintensiteiten.
    2. Bereken met behulp daarvan hun gezamenlijke geluidsdrukniveau.
    De geluidshinder in de buurt van een snelweg hangt onder meer af van de afstand tot die weg. Voor niet te grote afstanden (van ongeveer 20 m tot 1000 m) wordt de formule: `L = L0 - 10 log(2pi R)` gebruikt, waarin `R` de afstand tot de as van de weg in m is en `L` het geluidsdrukniveau in dB is.
    `L_0` is het geluidsdrukniveau van het verkeer op de as van de weg.
    3. Als op 20 m een geluidsdrukniveau van 77 dB wordt gemeten, hoe groot is dan het geluidsdrukniveau op 100 m afstand van die weg?
    4. Op welke afstand van die weg is het geluidsdrukniveau 60 dB?
    5. Geef de formule voor `L` als functie van R als `L(20) = 80` dB.

Testen

15. Bepaal van de volgende functies de afgeleide en los op `f'(x) = 10`.
    1. `f(x) = `³`log(x)`
    2. `f(x) = 2 log(11 - x)`
    3. `f(x) = ln(x/4)`


16. Gegeven is de functie `f(x) = (2 + 2 ln(x))/x`.
    1. Bereken algebraïsch de karakteristieken van de grafiek van `f`.
    2. Bereken de coördinaten van het buigpunt van de grafiek van `f`.
    3. De raaklijn in een punt `P` van de grafiek van `f` gaat door `O(0,0)`. Bereken de hoek die deze raaklijn met de positieve `x`-as maakt.



17. Helderheid van sterren

    De helderheid van sterren wordt vanouds aangegeven door de grootteklasse of magnitude `m`. Heldere sterren zijn van de eerste grootte: `m = 1`. Sterren die met het blote oog nog net zichtbaar zijn, hebben magnitude 6. Die magnitude wordt echter nog fijner onderverdeeld. De ster "Castor" in het sterrenbeeld "Tweelingen" heeft een magnitude van 1,58.
    Volgens de wet van Fechner is de magnitude afhankelijk van de lichtsterkte l volgens de formule: `m = a ln(l) + b`.
    Daarin is de lichtsterkte van een ster met magnitude 6 gelijk aan 1: dus voor `l = 1` geldt `m = 6`. Een ster van de eerste grootte is echter 100 keer zo lichtsterk: dus voor `l = 100` geldt `m = 1`.
    1. Bereken met behulp van deze gegevens `a` en `b`.
    2. Voor de ster "Regulus" geldt dat `l = 73`. Bereken de magnitude van Regulus.
    3. De helderste ster is "Sirius" met een magnitude van `m = -1,6`. Bereken de bijbehorende lichtsterkte.
    4. Schrijf `l` als functie van `m`.
    De lichtsterktes van twee sterren die samen een dubbelster vormen kun je optellen, hun magnitudes echter niet. De ster ε in het sterrenbeeld "Lier" is zo’n dubbelster. De magnitudes van de afzonderlijke sterren zijn 4,5 en 4,7.
    5. Hoe groot is de magnitude van de dubbelster?