Exponentiële functies

Inleiding

Je hebt het getal e leren kennen en de natuurlijke logaritme.
Je kunt nu functies van de vorm f(x) = e^x differentiëren. Maar je wilt ook f(x) = g^x en alle functies waarin g^x in het voorschrift voorkomt kunnen differentiëren. Dan kun je van dit soort functies de karakteristieken berekenen met behulp van de afgeleide en de tweede afgeleide.

Je leert nu:

• de afgeleide van f(x) = g^x bepalen
• de regels voor het differentiëren toepassen op functies waarin de onbekende in de exponent voorkomt;
• van dergelijke functies de hellingen, de extremen en de buigpunten berekenen.

Je kunt al:

• exponenten en logaritmen gebruiken;
• differentiëren met alle basisregels en dit toepassen bij het berekenen van hellingen, extremen en buigpunten;
• de afgeleide van f(x) = e^x bepalen.

Verkennen

Je wilt f(x) = 2^x differentiëren.
Je weet dat de afgeleide van y = e^x is y' = e^x.
Verder ken je de eigenschappen van exponenten en logaritmen.

> Leg uit waarom 2 = e^ln(2).
> Laat zien, dat f(x) = e^ln(2) · x.
> Differentieer nu f met behulp van de kettingregel.
> Welke afgeleide heeft f(x) = 2^x?

Uitleg

Je wilt f(x) = 2^x differentiëren.
Je weet dat de afgeleide van y = e^x is y' = e^x.
Verder ken je de eigenschappen van exponenten en logaritmen.

Met behulp van deze eigenschappen kun je van grondtal veranderen.
In het algemeen is g^glog(2) = 2.
Dit geldt ook voor grondtal g = e, dus e^ln(2) = 2.

Hieruit volgt: f(x) = (e^ln(2))^x = e^ln(2) · x.
Nu kun je f met behulp van de kettingregel differentiëren, het grondtal is nu namelijk e.
Je vindt: f'(x) = e^ln(2) · x · ln(2).
En dit kun je weer schrijven als f'(x) = 2^x · ln(2).

Deze redenering kun je ook op elk ander grondtal toepassen. Doe je dit op grondtal g dan blijkt de afgeleide van f(x) = g^x te zijn: f'(x) = g^x · ln(g).

‡

Opgaven

1. In de Uitleg wordt de afgeleide van `f(x) = 2^x` bepaald.
   1. Bepaal op dezelfde manier de afgeleide van `g(x) = 3^x`.
   2. Bepaal op dezelfde manier de afgeleide van `h(x) = 0,5^x`.
   3. Bepaal nu zelf de afgeleide van `f(x) = g^x`.


2. Je hebt in de voorgaande opgave de afgeleide van `f(x) = g^x` bepaald.
   Ga na dat deze afgeleide ook geldt voor `f(x) = text(e)^x`.
   

Theorie

Voor de afgeleide van de exponentiële functie geldt:

• Als f(x) = g^x dan is f'(x) = g^x · ln(g).

Hierbij maak je gebruik van het veranderen van grondtal: g = e^ln(g).
Dit is één van de definitieformules van logaritmen, toegepast op het getal e.

Hiermee kun je elke exponentiële functie N met groeifactor g per tijdseenheid t op meerdere manieren schrijven:

• N(t) = N(0) · g^t
• N(t) = N(0) · e^kt waarin k = ln(g)
• N(t) = N(0) · 10^kt waarin k = log(g)

Dat is handig als je met meerdere exponentiële functies met verschillende groeifactoren te maken hebt. Je kunt ze dan toch steeds hetzelfde grondtal geven, e of 10.

Verder kun je nu allerlei functies waarin vormen als e^x en/of g^x voorkomen differentiëren met de differentieerregels. Daarmee kun je van functies die ingewikkelder zijn dan zuiver exponentiële functies ook de karakteristieken bepalen.

‡

Voorbeeld 1

In dit voorbeeld gaat het om het differentiëren van exponentiële functies met behulp van de differentieerregels die je tot nu toe hebt geleerd. Probeer eerst zelf de juiste afgeleiden te vinden (opgave 3) en bekijk daarna pas de oplossingen. Ga naar

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Toegepaste analyse > Exponentiële en logaritmische functies > Exponentiële functies > Voorbeeld 1

‡

Voorbeeld 2

Radioactieve stoffen zijn stoffen die straling uitzenden. Bij dergelijke stoffen zijn de atoomkernen instabiel, bijvoorbeeld doordat er te veel protonen en/of neutronen in zitten. Een natuurlijke radioactieve stof is de radiumisotoop ²²⁶₈₈Ra. Bij deze stof zend elke atoomkern een α-deeltje (een heliumkern) uit, waardoor hij overgaat in een atoom van het element radon: ²²²₈₆Rn. De halfwaardetijd van dit radium is ongeveer 1600 jaar. In die tijd wordt de helft van de radiumatomen omgezet in radon. Het percentage radium neemt voortdurend af (vanaf 100%).
Beschrijf het verval van radium op drie manieren met een formule.

Antwoord

Neem nu t = 0 op 1-1-1900 en t in jaren en noem het percentage radium N. Het verval van dit radium kun je nu beschrijven met een formule van de vorm:

• N(t) = N(0) · g^t met N(0) = 100 en g¹⁶⁰⁰ = 0,5.
  Dit wordt: N(t) ≈ 100 · 0,9996^t
• N(t) = N(0) · e^kt met N(0) = 100 en e^1600k = 0,5.
  Dit wordt: N(t) ≈ 100 · e^–0,00043t
• N(t) = N(0) · 10^kt met N(0) = 100 en 10^1600k = 0,5.
  Dit wordt: N(t) ≈ 100 · e^–0,00019t

‡

Voorbeeld 3

Bereken algebraïsch de extremen van de functie f met f(x) = (x² + 2x) · e^–x.

Antwoord

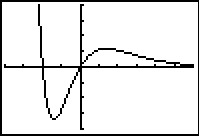
Bekijk eerst zelf de grafiek van f, bijvoorbeeld met de GR.

f'(x) = (2x + 2) · e^–x + (x² + 2x) · e^–x · –1 = (2 – x²) · e^–x.

Voor de extremen los je op: f'(x) = 0.
Ga na, dat je vindt: x = –$\sqrt{2}$  V  x = $\sqrt{2}$.
De extremen zijn: min.f(–$\sqrt{2}$) = (2 – 2$\sqrt{2}$)e^$\sqrt{2}$ en max.f($\sqrt{2}$) = (2 + 2$\sqrt{2}$)e^{–$\sqrt{2}$}.

‡

Opgaven

3. Probeer bij de functies in Voorbeeld 1 eerst zelf de afgeleiden te vinden.
   Gebruik alle tot nu toe geleerde differentieerregels. Controleer pas je antwoord als je ze allemaal hebt gemaakt. Heb je fouten gemaakt? Bekijk dan goed wat je fout deed!
   


4. Bepaal de afgeleide van:
   1. `f(x) = 5 * 3^x`
   2. `f(x) = 5 * 2^(0,5x)`
   3. `f(x) = 50 - 48 * 10^(0,1x)`
   4. `f(x) = 100text(e)^(-0,1x) + 200`


5. Bekijk Voorbeeld 2.
   1. Reken de drie gevonden vervalformules zelf na.
   2. Bereken met elk van de drie gevonden vervalformules de vervalsnelheid op `t = 0`.
   3. Bereken ook de vervalsnelheid op `t = 90`. Wat gebeurt er met de vervalsnelheid als `t` toeneemt?
   4. In welk jaar is er nog 20% van de beginhoeveelheid radium over als er verder niemand aan komt?


6. Differentieer de volgende functies en stel de vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 1`.
   1. `f(x) = 4 * 3^(2x - 4) - 12`
   2. `f(x) = (text(e)^(2x) - 1)/(text(e)^x)`
   3. `f(x) = text(e)^(1/x)`
   4. `f(x) = (text(e)^(-x^2))/(x^3)`


7. Gegeven is de functie `f` met `f(x) = xtext(e)^(-x)`.
   1. Bereken algebraïsch alle karakteristieken van de grafiek van `f`. Bekijk eventueel eerst Voorbeeld 3.
   2. Bereken het buigpunt van de grafiek van `f` en stel een vergelijking op van de raaklijn aan de grafiek in dit buigpunt.
   De functie `f_a` wordt gegeven door `f_a(x) = axtext(e)^(-x)`.
   3. Hebben alle functies `f_a` een uiterste waarde? Zo ja, druk die uiterste waarde dan uit in `a`.
   4. Op welke rechte lijn liggen alle toppen van functies `f_a`?
   5. Voor welke `a` is de uiterste waarde van `f_a` gelijk aan `80`?
   6. Voor welke `a` gaat de raaklijn aan de grafiek van `f_a` in `(0,0)` ook door het punt `(2,15)`?
   7. Voor welke `a` ligt het buigpunt van de grafiek van `f_a` op de lijn `y = 20`?


8. Bij benzinestations is vaak een extra service beschikbaar om de autobanden op te pompen. De automatische pomp levert een druk van 3,5 atmosfeer. De luchtdrukverandering in de band is recht evenredig met het drukverschil tussen de luchtdruk in de band en de luchtdruk van de pomp. De luchtdruk in de band begint met 1,4 atmosfeer en is na 10 seconden pompen opgelopen tot 2,0 atmosfeer.
   1. De luchtdruk `p` in de band (in atmosfeer) hangt gedurende het oppompen af van de tijd `t` in seconden. Schets een passende grafiek bij dit verband.
   `p(t)` kan worden beschreven door een formule van de vorm: `p(t) = 3,5 - a * g^t`.
   2. Bereken `a` en `g`.
   3. Je stopt de pomp als de druk in de band 2,6 atmosfeer bedraagt. Na hoeveel seconden is dat het geval?
   4. Bereken de snelheid waarmee de druk in de band toeneemt op `t = 0`.


9. Zowel in de atmosfeer als in levende organismen bevindt zich een bepaald percentage aan radioactieve koolstof C-14. Zodra een organisme sterft vindt er geen uitwisseling met de koolstof uit de atmosfeer meer plaats. Het percentage C-14 neemt vanaf dat moment exponentieel af met een halveringstijd van ongeveer 5600 jaar. Omdat alle levende organismen eenzelfde gehalte aan C-14 hebben, stelt dit ons in staat de ouderdom te bepalen van natuurlijke materialen als perkament, leren kleding, houten palen en dergelijke.
   Het gehalte `C(t)` aan C-14 is gegeven als percentage van het gehalte in levende organismen. `t` is de tijd in jaren met `t = 0` op het moment dat het organisme is gestorven.
   1. Stel een formule op voor `C(t)` van de vorm `C(t) = 100 * text(e)^(kt)`. Bereken `k` in zes decimalen nauwkeurig.
   2. Van de Dode-Zeerollen is het gehalte aan C-14 nog 79%. Hoe oud zijn ze?
   3. Van een mummie is nog 65% van het gehalte aan C-14 over. Hoe oud is die mummie?
   4. Van een Indianensandaal uit een grot in Amerika is nog 33% van het gehalte aan C-14 over. Hoe oud is die sandaal?

Verwerken

10. Bekijk de grafiek van de functie `f` met `f(x) = x + 2^(-x)`.
    1. Bereken het minimum van de grafiek van `f` in twee decimalen nauwkeurig.
    2. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 0`.


11. Gegeven is de functie `f` met `f(x) = xtext(e)^(-x^2)`.
    1. Bereken algebraïsch de karakteristieken van de grafiek van `f`.
    2. Bereken de buigpunten van de grafiek van `f`.
    3. De lijn met vergelijking `y = px` heeft precies één punt met de grafiek van `f` gemeen. Welke waarden kan `p` aannemen?


12. Gegeven een familie van functie `f_p` door `f_p(x) = (x - p)^2 text(e)^x`, waarin `p > 0`.
    1. Bereken algebraïsch de karakteristieken van `f_0`.
    2. Bereken het snijpunt van de grafieken van `f_0` en `f_1`.
    3. Het snijpunt van de grafieken van `f_0` en `f_p` ligt op de lijn `y = 1`. Bepaal voor welke `p` dit het geval is.
    4. Toon aan dat `f_p` precies één maximum heeft en druk dit maximum uit in `p`.
    5. Onderzoek hoeveel buigpunten de grafieken van `f_p` hebben.


13. Melk bewaar je in de koelkast op een temperatuur van 6°C. Als je een glas melk inschenkt heeft dit op `t = 0` dan ook deze temperatuur. Vanaf dat moment warmt de melk op tot kamertemperatuur, zeg 20°C. Die opwarming gaat volgens de warmtewet van Newton zo, dat de snelheid van opwarmen recht evenredig is met het temperatuursverschil met de omgeving.
    1. Maak een schets van het verloop van de temperatuur `T` van de melk als functie van de tijd `t` in minuten.
    2. Leg uit dat de functie `T` die de temperatuur van de melk in het glas beschrijft moet voldoen aan `T'(t) = c * (T(t) - 20)`.
    3. Toon aan dat een functie van de vorm `T(t) = 20 + a * text(e)^(ct)` voldoet.
    4. Neem aan, dat na 12 minuten de melk is opgewarmd tot 18°C. Stel een daarbij passende formule voor `T(t)` op.
    5. Bereken de opwarmsnelheid van de melk op `t = 0` en op `t = 15`. Verklaar het verschil tussen beide waarden.


14. Bij onderzoek in het menselijk lichaam gebruiken artsen de stof jodium-131. Die stof is namelijk radioactief en daardoor kunnen deeltjes van die stof in het menselijk lichaam van buitenaf worden gevolgd. De halveringstijd (of halfwaardetijd) van jodium-131 is 8,06 dagen. Omdat radioactief verval exponentieel verloopt, kan de hoeveelheid jodium-131 in mg worden beschreven door:

    `m = m_0 * text(e)^(-kt)`

    `t` is daarin de tijd in dagen en `m_0` is de hoeveelheid op tijdstip `t = 0`.
    1. Bereken `k`, dat is de zogenaamde desintegratieconstante.
    2. Als iemand een stof krijgt ingespoten die 5,00 mg jodium-131 bevat, hoeveel is daar na 15 dagen dan nog van terug te vinden?
    3. Toon aan dat in dit model de vervalsnelheid recht evenredig is met de hoeveelheid radioactieve stof. Hoe groot is de bijbehorende evenredigheidsconstante?
    4. Na hoeveel dagen is er nog 10% van de beginhoeveelheid over?
    5. Na hoeveel dagen is de vervalsnelheid (de radioactiviteit) verminderd tot 10% van de beginsnelheid?
    6. Als een meetnauwkeurigheid van twee decimalen maximaal haalbaar is, na hoeveel dagen is de ingespoten 5 mg jodium-131 dan niet meer meetbaar?
    7. Is de stof ooit volledig verdwenen?

Testen

15. Differentieer de volgende functies en stel een vergelijking op van de raaklijn aan de grafiek van `f` in het snijpunt met de `x`-as. Geef de raaklijn met benaderingen in twee decimalen nauwkeurig.
    1. `f(x) = 3 * 0,5^(2x - 1) - 4`
    2. `f(x) = 5 - text(e)^(sqrt(x))`


16. Bij het maken van foto’s van je gebit gebruikt de tandarts röntgenstraling. De patiënt krijgt een heel geringe dosis straling toegediend en ondervindt daarvan geen nadelige gevolgen. Maar een tandarts die dit regelmatig doet krijgt te maken met een opeenhoping van straling in zijn lichaam. Daarom beschermt hij zich met behulp van een loden plaat.
    De intensiteit van de straling neemt namelijk af in een stof als lood. Als die stralingsintensiteit wordt voorgesteld door `I`, dan geldt:

    `I(d) = I(0) * text(e)^(-alpha * d)`

    waarin `d` de dikte van de loden plaat in cm is en `alpha` een constante is die afhangt van het materiaal.
    1. Een loden plaat van 1 cm dik houdt ongeveer 60% van de straling tegen. Bereken de materiaalconstante `alpha`.
    2. Hoe dik moet een loden plaat zijn om 99% van de straling tegen te houden?
    3. Hoeveel bedraagt de snelheid waarmee de stralingsintensiteit afneemt op het moment dat die straling de loden plaat bereikt?