Het getal e

Inleiding

Je kunt functies van de vorm f(x) = g^x nog niet differentiëren. Daar ga je nu wat aan doen. Je kunt dan tenminste iets zeggen over de veranderingssnelheid van groeiprocessen.
Bij het differentiëren van exponentiële functies speelt het getal e een belangrijke rol. Daarmee ga je dan ook uitgebreid kennis maken.

Je leert nu:

• de afgeleide van exponentiële functies bepalen;
• het getal e gebruiken bij het bepalen van die afgeleide.

Je kunt al:

• exponenten en logaritmen gebruiken;
• differentiëren met alle basisregels en dit toepassen bij het berekenen van hellingen, extremen en buigpunten.

Verkennen

Met je grafische rekenmachine kun je een functie `f(x)` en een benadering voor de afgeleide van deze functie vergelijken. Daarbij maak je gebruik van het feit dat `f'(x)` kan worden benaderd door de veranderingssnelheid bij een hele kleine toename van `x`.

Voer in je grafische rekenmachine in:
Y1 = 2^X
Y2 = (Y1(X + 0.001) – Y1(X))/0.001
Y3 = Y2/Y1
Gebruik de standaardinstellingen van het venster.

> Leg uit dat Y2 een benadering is van de afgeleide van Y1.
> Wat valt op als je de grafiek van Y2 vergelijkt met die van Y1?
> Hoe kun je nu de grafiek van Y3 verklaren?
> Welke conclusie trek je? Geldt dit ook voor `f(x) = 3^x`? En voor andere exponentiële functies?
> Geldt dit ook voor `f(x) = x^2`? En voor `f(x) = x^3`?

Uitleg

Bij exponentiële groei gaat het om functies van de vorm
f(x) = b · g^x. Neem je b = f(0) = 1, dan hebben deze functies de vorm f(x) = g^x. Ga na dat de helling van de grafiek, de groeisnelheid per eenheid, af hangt van de grootte van g. Neem je bijvoorbeeld x = 1, dan zie je de helling groter worden als g groter wordt.
Neem je bijvoorbeeld g = 2 dan zie je dat de helling voor elke x recht evenredig is met f(x): f'(x) = c · g^x.

• Voor g = 2 geldt: c ≈ 0,69.
  Dus als f(x) = 2^x dan is f'(x) = 0,69 · 2^x.
• Voor g = 3 geldt: c ≈ 1,10.
  Dus als f(x) = 3^x dan is f'(x) = 1,10 · 3^x.

Er lijkt een waarde van g te bestaan (tussen 2 en 3) waarvoor geldt dat c = 1. Ga na, dat dit bij g ≈ 2,7 het geval is. Het getal waarbij dit precies het geval heet, is net zo'n bijzonder getal als π. Dit getal heeft de letter e gekregen: e ≈ 2,71828...
Voor dit getal geldt: als f(x) = e^x, dan is f'(x) = e^x.

Met f(x) = e^x reken je net als met alle exponentiële functies. Er hoort dus ook een logaritme met grondtal e bij...

‡

Opgaven

1. Lees eerst de Uitleg goed door. In het algemeen geldt: Als `f(x) = g^x` dan is `f'(x) = c * g^x`.
   1. Bekijk de grafiek van `f(x) = 3^x` en (een benadering van) zijn afgeleide. Laat zien dat `f'(x) ~~ 1,10 * 3^x`, dus `c ~~ 1,10`.
   2. Bekijk de grafiek van `f(x) = 2,5^x` en (een benadering van) zijn afgeleide. Bepaal nu zelf de bijpassende waarde van `c`.
   3. Doe ditzelfde ook voor `f(x) = 2,7^x` en `f(x) = 2,8^x`.
   4. Is er een getal `g` waarvoor `c = 1`? Hoe groot is dit getal ongeveer?


2. Gegeven de functie `f(x) = g^x`.
   De verandering van `f` op een klein interval `[x, x + h]` is: `(Deltay)/(Deltax) = (g^(x + h) - g^x)/(h)`.
   1. Leg dat met behulp van een figuur uit. (Maak eventueel een eigen applet in GeoGebra!)
   2. Laat zien, dat `(Delta y)/(Delta x) = (g^(h) - 1)/(h) * g^x`.
   3. Waarom kun je hieruit afgeleiden dat `f'(x) = c * g^x`?
   4. Neem `g = text(e)` en bepaal met behulp van het antwoord van b de waarde van e.


3. Bekijk de grafiek van de functie `f(x) = text(e)^x`.
   1. Hoe voer je die grafiek in je grafische rekenmachine in?
   2. Welke asymptoot heeft die grafiek?
   3. Waar in de grafiek vind je het getal e?
   4. Los op `text(e)^x = 10`. Geef je antwoord in twee decimalen nauwkeurig.
   5. De oplossing van `text(e)^x = 10` is gelijk aan `x = ^(text)e log(10)`. Laat zien dat je zo dezelfde waarde voor `x` vindt als bij c.
   In plaats van ^elog(...) wordt in de wiskunde ln(...) gebruikt. Je rekenmachine heeft een speciale toets voor ln(...).
   6. Los nu zowel exact als in drie decimalen nauwkeurig op: `text(e)^x = 20`.
   7. Los op: `1/50 <= text(e)^x <= 50`. Geef benaderingen in drie decimalen nauwkeurig.
   8. Welk hellingsgetal heeft de grafiek van `f(x) = text(e)^x` in het punt `(1,e)`?
   9. Stel een vergelijking op van de raaklijn in dat punt.

Theorie

De afgeleide van de exponentiële functie f(x) = g^x vind je door de functie met een factor afhankelijk van g te vermenigvuldigen.
Als f(x) = g^x dan is f'(x) = c_g · g^x.

Er bestaat een waarde van g waarvoor geldt dat c_g = 1.
Deze natuurlijke groeifactor is het getal e.
Een benadering voor e is: e ≈ 2,71828...

Als f(x) = e^x, dan is f'(x) = e^x.

Met f(x) = e^x reken je net als met alle exponentiële functies. Op je rekenmachine zit er een speciale toets voor. En er hoort ook een logaritme met grondtal e bij...

Ook nu is e^x = a gelijkwaardig met x = ^elog(a).
In plaats van ^elog(a) schrijf je ln(a).
ln(a) is de natuurlijke logaritme van a.
De functies y = e^x en y = ln(x) zijn elkaars inverse functies. De grafieken daarvan zijn elkaars spiegelbeeld bij spiegelen in de lijn y = x.

‡

Voorbeeld 1

Maak met je grafische rekenmachine de grafiek van f(x) = e^x.
Stel een vergelijking op van de raaklijn aan de grafiek van f voor x = 2.
Los op: e$\sqrt{\text{e}}$ ≤ f(x) ≤ 5.

Antwoord

f'(x) = e^x, dus f'(2) = e².
Verder is f(2) = e².
De vergelijking van de raaklijn is daarom y = e²x – e².

Om de ongelijkheid op te lossen, moet je de waarden van x bepalen waarvoor

• e^x = e$\sqrt{\text{e}}$ = e^1,5, dit geeft: x = 1,5
• e^x = 5, dit geeft: x = ln(5)

de oplossing van de gegeven ongelijkheid is 1,5 ≤ x ≤ ln(5).

‡

Voorbeeld 2

Bekijk met je grafische rekenmachine de grafiek van f(x) = ln(x).
Bepaal de karakteristieken van f en los op: f(x) ≤ 10.

Antwoord

Omdat ln(x) = ^elog(x) moet ook nu x > 0.
D_f = $\langle \mathrm{0,}\to \rangle$ en B_f = $ℝ$.
de verticale asymptoot is x = 0.

f(x) = 10 geeft x = e¹⁰ want de e-macht en de natuurlijke logaritme zijn elkaars inverse.
Uit de grafiek lees je de oplossing van de ongelijkheid af: 0 < x ≤ e¹⁰.

‡

Voorbeeld

Gegeven is de functie f met voorschrift f(x) = e^2x – 3 e^x.
Bereken algebraïsch het bereik van f.

Antwoord

f'(x) = 2 e^2x – 3 e^x = 0 als e^x(2 e^x – 3) = 0, dus als e^x = 0  V  e^x = 1,5.
Hieruit volgt: x = ln(1,5).

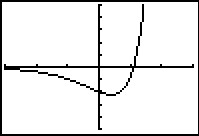Aan de grafiek van f zie je dat er een minimum zit bij x = ln(1,5).
Nu is f(1,5) = (e^ln(1,5))² – 3 e^ln(1,5) = –2,25.
En dus is: B_f = $[-\mathrm{2,25};\to \rangle$.

‡

Opgaven

4. Bekijk Voorbeeld 1.
   1. Stel de vergelijking van de raaklijn aan de grafiek van `f` voor `x = 3` op.
   2. Bekijk de oplossing van de gegeven ongelijkheid. Ga met behulp van de grafiek van `f` na dat deze juist is.
   3. Los nu zelf op: `e^(-20) < f(x) <= 20`.


5. Los de volgende vergelijkingen algebraïsch op:
   1. `2^x = 1/(8 sqrt(2))`
   2. `text(e)^x = 1/(text(e)^3 sqrt(text(e)))`
   3. `5text(e)^x = 125`
   4. `8text(e)^x = (2text(e) sqrt(text(e)))^3`


6. Bekijk Voorbeeld 2.
   1. Waar in de grafiek van `f(x) = ln(x)` vind je het getal e?
   2. Leg uit hoe je het domein en het bereik van `f` kunt afleiden uit het domein en het bereik van `g(x) = text(e)^x`.
   3. Voor welke waarde van `x` is `ln(x) = 5`? Geef je antwoord exact en in één decimaal nauwkeurig.
   4. Los op: `-5 <= ln(x) <= 5`. Geef benaderingen in twee decimalen nauwkeurig.


7. Bepaal de afgeleide van de volgende functies. Maak gebruik van alle bekende differentieerregels. Bepaal ook het bereik van `f`. Bekijk eventueel eerst Voorbeeld 3.
   1. `f(x) = 100 - 2 * text(e)^x`
   2. `f(x) = text(e)^(3x)`
   3. `f(x) = text(e)^(3 - x)`
   4. `f(x) = x text(e)^x`
   5. `f(x) = x/(text(e)^x)`
   6. `f(x) = text(e)^(x^2)`


8. Bij het afkoelingsproces van een kop koffie geldt `V'(t) = c * V(t)`, waarin `V` het temperatuursverschil met de omgeving, `t` de tijd (in minuten) en `c` een constante is.
   1. Laat zien dat een functie zoals `V(t) = text(e)^t` aan deze vergelijking voldoet voor elke `t`. Welke waarde heeft `c` dan?
   2. Waarom kan deze functie geen afkoelingsproces beschrijven?
   3. De afgeleide van `f(t) = (0,5)^t` is gelijk aan `f'(t) = c * (0,5)^t`. Bepaal met de grafische rekenmachine de waarde van `c` in twee decimalen nauwkeurig.
   4. Laat zien, dat een functie zoals `V(t) = 80 * (0,5)^t` ook voor elke `t` (bij benadering) voldoet aan de vergelijking hierboven.
   5. Waarom kan deze functie wel een afkoelingsproces beschrijven?


9. Los algebraïsch op en geef een benadering in twee decimalen nauwkeurig.
   1. `text(e)^(2x) = 0,05`
   2. `ln(x) = 2,06`
   3. `3text(e)^(4x) = 10`


10. Het is nuttig om de rekenregels voor exponentiële en logaritmische functies nog een keer te oefenen. Nu gebruik je daarbij (ook) het nieuwe grondtal e. Je vindt ze via

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Exponentiële functies > Exponenten en machten > Theorie
    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Functies en grafieken > Logaritmische functies > Eigenschappen > Theorie

    Druk bij de volgende formules `y` uit in `x` en vereenvoudig de uitdrukking.
    1. `text(e)^y = 2 * text(e)^x`
    2. `2 * text(e)^(2y) = x^3`
    3. `x = 2 * ln(y) + 3`
    4. `x = 2 * ln(y + 3)`
    5. `ln(y) + 2 * ln(x) = 1`
    6. `(ln(y) + 2) * ln(x) = 1`
    7. `(sqrt(text(e)))^y = 4x`
    8. `(1/(text(e)))^y = 4text(e)^x`

Verwerken

11. Gegeven is de functie `f(x) = 4text(e)^(-0,5x) - 2`.
    1. Welke asymptoot heeft de grafiek van deze functie?
    2. Bereken met behulp van logaritmen het snijpunt van de grafiek van `f` met de `x`-as.
    3. Bepaal de afgeleide van `f` en stel een vergelijking op van de raaklijn aan de grafiek van `f` in het snijpunt van de grafiek van `f` met de `x`-as.
    4. Los op: `f(x) < -1`.


12. Gegeven is de functie `f(x) = 4 ln(-0,5x) - 2`.
    1. Welke asymptoot heeft de grafiek van deze functie?
    2. Schrijf het domein en het bereik van `f` op.
    3. Bereken met behulp van exponenten het snijpunt van de grafiek van `f` met de `x`-as.
    4. Los op: `f(x) < -1`.


13. Los de volgende vergelijkingen algebraïsch op en benader zo nodig de antwoorden in drie decimalen nauwkeurig.
    1. `text(e)^x = 3`
    2. `text(e) * x = 3`
    3. `x^(text(e)) = 3`
    4. `ln(x) = 3`
    5. `log(x) = 3`
    6. `2 * text(e)^(0,1x - 5) = 40`
    7. `2 ln(0,1x - 5) = 40`


14. Los de volgende vergelijkingen algebraïsch op en benader zo nodig de antwoorden in drie decimalen nauwkeurig.
    1. `text(e)^(2x) * text(e)^(x - 6) = 1`
    2. `text(e)^(2x) - text(e)^(x - 6) = 0`
    3. `ln(2x) - ln(x - 6) = 1`
    4. `ln(2x) * ln(x - 6) = 0`
    5. `2^x = text(e)^(x + 2)`
    6. `ln(ln(2x)) = 1`
    7. `3 text(e)^x = 15text(e)^(2 - x)`
    8. `text(e)^x - 2text(e)^(-x) = 1`


15. Druk `N` zo eenvoudig mogelijk uit in `t`:
    1. `ln(N) = 2 * ln(t) - 3`
    2. `log(N) = 2 * log(t) - 3`
    3. `text(e)^(2N) = t + 2`
    4. `10^(2N) = t + 2`
    5. `ln(N) = 2t - 3`
    6. `text(e)^t = 2N - 3`


16. Toon aan dat de volgende formules waar zijn voor elke waarde van `x`.
    1. `(1/(text(e)))^x = text(e)^(-x)`
    2. `text(e)^(2 ln(x)) = x^2`
    3. `text(e)^(ln(x) + ln(2)) = 2x`
    4. `text(e)^(2 - ln(x)) = (text(e)^2)/x`


17. Een kop koffie uit een automaat heeft een temperatuur van 80?C op het moment dat hij wordt ingeschonken. Hij koelt af volgens de formule:

    `T(t) = 20 + 60 * (0,8)^t`

    Hierin is `T` de temperatuur van de koffie en `t` de tijd in minuten vanaf het moment van inschenken.
    1. Ga na dat de koffie volgens de formule bij het inschenken een temperatuur van 80°C heeft.
    2. Hoeveel bedraagt de omgevingstemperatuur?
    3. De afgeleide van `f(t) = (0,8)^t` is `f'(t) = c * (0,8)^t`. Bepaal met je grafische rekenmachine de bijpassende waarde van `c`.
    4. Volgens de warmtewet van Newton is de snelheid waarmee de temperatuur verandert recht evenredig met het temperatuursverschil met de omgeving. Laat met behulp van een berekening zien dat de gegeven functie `T` aan de warmtewet van Newton voldoet.
    5. Hoe kun je aan de afgeleide van `T` zien dat er inderdaad van afkoeling sprake is?

Testen

18. Gegeven is de functie `f(x) = 8 - 4 text(e)^x`.
    1. Welke asymptoot heeft de grafiek van deze functie?
    2. Bereken met behulp van logaritmen het snijpunt van de grafiek van `f` met de `x`-as.
    3. Bepaal de afgeleide van `f` en stel een vergelijking op van de raaklijn aan de grafiek van `f` in het snijpunt van de grafiek van `f` met de `x`-as.
    4. Los op: `f(x) >= 2`.


19. Gegeven is de functie `g(x) = 8 - 4 ln(x)`.
    1. Welke asymptoot heeft de grafiek van deze functie?
    2. Bereken algebraïsch het snijpunt van de grafiek van `g` met de `x`-as.
    3. Los op: `g(x) < 2`.


20. Druk `N` zo eenvoudig mogelijk uit in `t`.
    1. `5 text(e)^N = 2t + 10`
    2. `5 ln(N) = 2t + 10`
    3. `ln(N) = 0,01 ln(t) + 1,15`


21. Los de volgende vergelijkingen algebraïsch op:
    1. `10 text(e)^(x - 2) = 5 text(e)(4x)`
    2. `ln(x) + ln(x + 2) = 1`


22. Differentieer:
    1. `f(x) = text(e)^x - 3text(e)^(2x)`
    2. `f(x) = x^2 text(e)^(x)`