Totaalbeeld

Samenvatten

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Integraalrekening > Totaalbeeld > Samenvatten


Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp "Integraalrekening". Een eigen samenvatting maken is nuttig.

Begrippenlijst:

41: het begrip integraal — het verband tussen integraal en oppervlakte
42: het begrip primitieve (functies)
43: de hoofdstelling van de integraalrekening — somregel, constante-regel en substitutieregel voor integreren
44: oppervlakte van een vlakdeel ingesloten door grafieken en lijnen
45: omwentelingslichaam — inhoud van een omwentelingslichaam

Activiteitenlijst:

41: de integraal van een functie op een bepaald interval berekenen
42: integralen berekenen door primitiveren
43: integreren met behulp van integreerregels en de hoofdstelling van de integraalrekening
44: de oppervlakte van vlakdelen berekenen door integreren, ook met de GR
45: inhoud van omwentelingslichamen berekenen, zowel bij wenteling om de x-as als bij wenteling om de y-as.

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Integraalrekening > Totaalbeeld > Achtergronden

Testen

Opgaven

  1. Gegeven is de functie `f(x) = -1/2 x + 4` op het interval `[-2,2]`.
    1. Verdeel het interval [-2,2] in vier gelijke deelintervallen, en bereken de onder- en de bovensom bij deze verdeling.
    2. Bereken het verschil tussen onder- en bovensom als je het interval in acht gelijke deelintervallen verdeelt.

  2. Bepaal de functie `F` waarvoor geldt:
    1. `F'(x) = x sqrt(x)` met `F(4) = 0`
    2. `F'(x) = 1/(sqrt(1 + 4x))` met `F(2) = 0`
    3. `F'(x) = 1/(x^2) + 1/((3 - 2x)^2)` met `F(2) = 0`

  3. Bepaal de volgende onbepaalde integralen:
    1. `int x^2 sqrt(2x) text(d)x`
    2. `int (x^2 - 4)^2 text(d)x`
    3. `int x sqrt(2 + x^2) text(d)x`

  4. Bereken het exacte antwoord van deze bepaalde integralen en controleer je antwoorden met de rekenmachine:
    1. `int_1^8 7 root[3](x) text(d)x`
    2. `int_0^2 2/((1 + 2x)^2) text(d)x`
    3. `int_1^4 3/(sqrt(x)) - 5 sqrt(x) text(d)x`

  5. Gegeven is de functie `f(x) = 1/2 x^2 - 3x + 4`.
    1. Bereken: `int_0^6 1/2 x^2 - 3x + 4 text(d)x`.
    2. Bepaal de oppervlakte van het gebied ingesloten door `f(x)` en de `x`-as op het interval `[0,6]`.
    3. Waarom heb je bij a en b niet hetzelfde antwoord gekregen? Verklaar het verschil.
    4. Bereken de lengte van de parabool tussen zijn twee snijpunten met de assen in twee decimalen nauwkeurig.

  6. Gegeven is de functie `f(x) = sqrt(3 - x)`.
    Er is een getal `a` zodat de oppervlakte van het gebied dat ingesloten wordt door de grafiek van `f` en de `x`-as op het interval `[a,3]` gelijk is aan `18`.
    1. Bereken `a`.
    Er is ook een getal `b` zodat de oppervlakte van het gebied ingeloten door de grafiek van `f` en de `x`-as op het interval `[0,b]` even groot is dan de oppervlakte van het gebied ingesloten door de grafiek van `f` en de `x`-as op het interval `[b,3]`.
    1. Benader b in twee decimalen nauwkeurig.

  7. Als je de grafiek van de functie `f(x) = 1/x` op het interval `[1, p]` wentelt om de `x`-as dan ontstaat een figuur met de vorm van een soort toeter.
    1. Laat zien dat de inhoud van deze toeter gelijk is aan: `I = pi * (1 - 1/p)`.
    Als `p` oneindig groot wordt dan ontstaat een oneindig lange toeter. Toch is de inhoud van deze toeter niet oneindig groot.
    1. Bepaal de inhoud van deze oneindige toeter.

  8. Gegeven is de functie `f` met `f(x) = x^3`.
    Door de grafiek op `[0,p]` om de `x`-as te wentelen ontstaat een omwentelingslichaam `a`.
    Door de grafiek op `[0,p]` om de `y`-as te wentelen ontstaat een omwentelingslichaam `b`.
    Beide omwentelingslichamen hebben hetzelfde volume. Bereken `p`.

  9. De punten `P(x,y)` die voldoen aan de vergelijking `x^2 + 4y^2 = 16` liggen op een ellips.
    1. Met welke twee functievoorschriften kun je deze ellips beschrijven?
    2. Bereken de oppervlakte van deze ellips in twee decimalen nauwkeurig.
    3. Bereken de omtrek van deze ellips in twee decimalen nauwkeurig.

  10. Benzineverbruik

    Een auto die met een snelheid van `20` m/s rijdt, trekt `5` seconden op met een versnelling van `2` m/s2. Na die `5` sesonden is de snelheid van de auto `30` m/s.
    1. Stel een formule op waarmee je de snelheid tijdens die `5` seconden kunt berekenen.
    2. Hoeveel meter legt de auto in die tijd s af?
    Het benzineverbruik van een auto is afhankelijk van de snelheid. Uit nauwkeurig onderzoek is gebleken dat het verbruik van een rijdende auto beschreven wordt door de formule: `N(v) = 1,3 * 10^(-7) * v^2 - 3,6 * 10^(-6) v + 10^(-4)` met `N` in L/m en `v` in m/s.
    1. Ga na dat de auto in 1 uur 5,75 liter benzine verbruikt als de snelheid tijdens dat uur 20 m/s is.
    Tijdens de eerste vijf seconden verandert de snelheid en dus ook het verbruik voortdurend. Het verbruik kun je benaderen als je de tijd verdeelt in 'kleine' stukjes `Delta t`. In zo’n klein tijdsinterval kun je de snelheid als constant beschouwen.
    1. Laat zien dat het verbruik in de tijdsperiode `[t, t + Delta t]` ongeveer gelijk is aan: `(1,3 * 10^(-7) * (20 + 2t)^2 - 3,6 * 10^(-6) * (20 + 2t) + 10^(-4)) * (20 + 2t) * Delta t`.
    2. Bereken met een integraal het benzineverbruik in die 5 seconden. Gebruik daarbij de grafische rekenmachine.

Toepassen

  1. Arbeid

    Lees over het begrip "arbeid" in de natuurkunde

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Integraalrekening > Totaalbeeld >Toepassingen

    Aan een veer hangt men een massa van 1 kg. Na enige tijd hangt de veer weer stil. Hij is dan 10 cm uitgetrokken. In de onderste stand werken er twee krachten op de massa: de zwaartekracht en de veerkracht. De zwaartekracht is bij benadering gelijk aan `m * g`. De veerkracht is recht evenredig met de uitwijking.
    1. Bereken de veerconstante `C`. Neem `g = 10` m/s2.
    Als je de veer verder naar beneden trekt, dan moet je een extra kracht uitoefenen.
    1. Hoe groot is die kracht als de veer 20 cm uitgetrokken is?
    2. Hoeveel arbeid vericht je als je de massa 30 cm vanuit de evenwichtsstand naar beneden trekt?

  2. Zwaartepunt

    Je weet waarschijnlijk wel wat het zwaartepunt van een voorwerp is. Je kunt het vaak gemakkelijk bepalen. Je houdt het object in een bepaald punt vast en trekt een (denkbeeldige) lijn naar beneden. Dat herhal je een paar keer met verschillende punten van vasthouden. Waar als die lijnen elkaar snijden bevindt zich het zwaartepunt.
    In sommige situaties kun je de coördinaten van het zwaartepunt uitrekenen. Bekijk

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Integraalrekening > Totaalbeeld > Toepassingen

    Ga er van uit dat het vlakdeel wordt begrensd door de `x`-as en een parabool met top `(6,4)` die door `(4,0)` en `(8,0)` gaat.
    1. Voer de berekening die daar wordt beschreven ook daadwerkelijk uit.
    2. Het antwoord van a mag je niet verrassen, hier was zo'n moeilijke berekening overbodig. Licht dat toe.
    Het berekenen van de `y`-waarde van het zwaartepunt gaat op een vergelijkbare manier. Maar nu heb je de functies `x = +-sqrt(4 - y) + 6` nodig. De formule voor de berekening van het zwaartepunt wordt nu

    `y_Z * int_0^4 c * 2sqrt(4-y) text(d)y = int_0^4 y * c * 2sqrt(4-y) text(d)y`

    1. Licht deze formule toe.
    2. Bereken met de grafische rekenmachine de `y`-waarde van het zwaartepunt van het gegeven vlakdeel.
    3. Bereken de coördinaten van het zwaartepunt van het gebied `G` dat wordt ingesloten door de parabool `y = 4 - x^2`, de parabool `y = 3 - x^2` en de `x`-as.
    Een geodriehoek is een gelijkbenige rechthoekige driehoek. Zo'n driehoek kun je zo in het assenstelsel leggen, dat `Delta ABC` met `A(-a,0)`, `B(a,0)` en `C(0,a)` ontstaat.
    1. Laat zien dat `ABC` inderdaad een gelijkbenige rechthoekige driehoek is.
    2. Bewijs nu met behulp van integreren dat het zwaartepunt `Z(0, 1/3 a)` is.

Examenopgaven

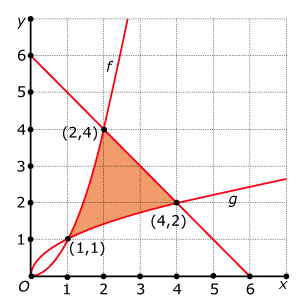
  1. Twee halve parabolen

    Gegeven zijn de functies `f(x) = x^2` en `g(x) = sqrt(x)`, beide met domein `[0,rarr:)`. De lijn `x = p`, met `0 < p < 1`, snijdt de grafiek van `f` in `A` en de grafiek van `g` in `B`.
    1. Bereken de exacte waarde van `p` waarvoor de lengte van het lijnstuk `AB` maximaal is.
    In de figuur zijn de grafieken van `f` en `g` en ook de lijn `y = 6 - x` getekend. Het gebied ingesloten door de grafiek van `f`, de grafiek van `g` en de lijn `y = 6 - x`, is in de figuur grijs gekleurd.
    1. Bereken algebraïsch de exacte oppervlakte van dit gebied.

    (bron: examen wiskunde B vwo 2004, tweede tijdvak)


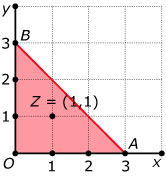
  2. Zwaartepunt

    De hoekpunten van driehoek `OAB` zijn `O(0,0)`, `A(3,0)` en `B(0,3)`.
    1. Toon met de formule voor het berekenen van een zwaartepunt aan dat het zwaartepunt van driehoek `OAB` het punt `(1,1)` is.
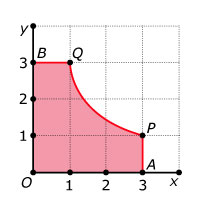
    Het vlakdeel `OAPQB` wordt begrensd door de `x`-as, de `y`-as, de lijn `x = 3`, de lijn `y = 3` en de hyperbool `y = 3/x`.
    1. Bereken de `x`-coördinaat van het zwaartepunt van dit vlakdeel in twee decimalen nauwkeurig.

    (bron: examen wiskunde B vwo 2001, tweede tijdvak, aangepast)


  3. Gebroken functie

    Gegeven is de functie `f(x) = x + 4/x`.
    1. Bereken langs algebraïsche weg de coördinaten van de toppen van de grafiek van `f`.
    `V` is het gebied dat wordt ingesloten door de lijn `y = 5` en de grafiek van `f`.
    1. Bereken de omtrek van `V` in twee decimalen nauwkeurig.

    (bron: examen wiskunde B vwo 2003, tweede tijdvak, aangepast)


  4. Onafhankelijk van `n`

    De grafieken van de functies `y = 1/2 x^2` en `y = x` sluiten een gebied `G` in. Door dit gebied `G` te wentelen om de `x`-as ontstaat een omwentelingslichaam.
    1. Bereken de exacte waarde van de inhoud van dit omwentelingslichaam.
    Voor `n = 1, 2, 3, ...` bekijken we het vierkant `OQ_nP_nR_n`, waarvan twee zijden langs de coördinaatassen vallen en waarvan het punt `P_n(n,n)` een hoekpunt is. De grafiek van de functie `y = 1/n x^2` gaat door `O` en door `P_n`. De richtingscoëfficiënt van de raaklijn aan de grafiek van `y = 1/n x^2` in het punt `P_n` is onafhankelijk van `n`.
    1. Toon dit aan.
    De grafiek van `y = 1/n x^2` verdeelt het vierkant `OQ_nP_nR_n` in twee stukken `V` en `W`.
    De verhouding van de oppervlakten van `V` en `W` is onafhankelijk van n.
    1. Toon dit aan.

    (bron: examen wiskunde B vwo 2005, eerste tijdvak, aangepast)