Omwentelingslichamen

Inleiding

Je ziet hier een draaibank. Er wordt een stuk hout bewerkt door het te draaien om een bepaalde as en dan met een beitel een kromme lijn te beschrijven. De omwenteling doet de rest...
Van het voorwerp dat zo ontstaat is (als het perfect is gelukt) elke doorsnede loodrecht op de draaias een cirkel. Je noemt zoiets een omwentelingslichaam.

Je leert nu:

• het begrip omwentelingslichaam;
• de inhoud van omwentelingslichamen berekenen met integreren zowel bij wentelen om de x-as als bij wentelen om de y-as.

Je kunt al:

• integralen bepalen met behulp van primitiveren;
• integralen bepalen met behulp van je grafische rekenmachine.

Verkennen

Een rechte kegel is een omwentelingslichaam.
Je kunt een kegel met een hoogte van 20 en een grondvlak met straal 5 maken door het vlakdeel ingesloten door de grafiek van f(x) = 0,25x en de x-as op het interval [0,20] te wentelen om de x-as.

> Maak een schets van deze kegel, uitgaande van de grafiek van f op het gegeven interval.
> Verdeel het interval in 10 deelintervallen. Je kunt het stukje kegel op het `k`de deelinterval benaderen door een cilinder met straal `f(0,2k)` en hoogte 0,2. Door de inhouden van die cilindretjes op te tellen krijg je een bovensom voor de inhoud van de kegel. Bepaal die bovensom. (Bekijk eventueel de bijbehorende animatie op de math4allsite.)
> Bepaal op dezelfde manier een ondersom voor de inhoud van de kegel.
> Hoe zou je met behulp van integreren de inhoud van de kegel kunnen berekenen?

Uitleg

Je ziet hier hoe het vlakdeel ingesloten door de grafiek van f(x) = $\sqrt{x}$  en de x-as op het interval [0,4] om de x-as wordt gewenteld.
Het omwentelingslichaam dat zo ontstaat kun je benaderen door smalle cilinders door [0,4] in deelintervallen met een breedte van Δx te verdelen. De inhoud van zo'n cilinder is πy² · Δx. De inhoud van het omwentelingslichaam benader je door Riemannsommen van de vorm:
$\overline{S_n}={\displaystyle \sum _{k=1}^n\text{π}\cdot {(f_{\max }(x))}^2\cdot \Delta x}$  en  $\underset{¯}{S_n}={\displaystyle \sum _{k=1}^n\text{π}\cdot {(f_{\min }(x))}^2\cdot \Delta x}$

Als het aantal deelintervallen oneindig groot wordt, dat gaat Δx naar 0.
De inhoud van het omwentelingslichaam wordt dan:
I = ${\displaystyle \underset{0}{\overset{4}{\int }}\text{π}\cdot {(f(x))}^2\text{d}x}$ = ${\displaystyle \underset{0}{\overset{4}{\int }}\text{π}\cdot {\sqrt{x}}^2\text{d}x}$ = ${\displaystyle \underset{0}{\overset{4}{\int }}\text{π}x\text{d}x}$ = ${\left[\frac{1}{2}\text{π}{x}^2\right]}_0^4$ = 8π

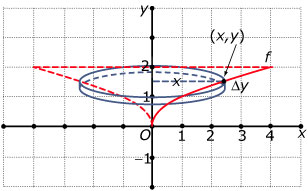
Je ziet hier hoe het vlakdeel ingesloten door de grafiek van f(x) = $\sqrt{x}$  en de y-as op het interval [0,4] om de y-as wordt gewenteld.
Dit vlakdeel wordt ook begrensd door de lijn y = 2. Het omwentelingslichaam dat zo ontstaat kun je benaderen door smalle cilinders door op de y-as het interval [0,2] in deelintervallen met een breedte van Δy te verdelen. De inhoud van zo'n cilinder is πx² · Δy.
Als het aantal deelintervallen oneindig groot wordt, dat gaat Δy naar 0 en de inhoud van het omwentelingslichaam wordt een integraal van de vorm:
I = ${\displaystyle \underset{0}{\overset{2}{\int }}\text{π}{x}^2\text{d}y}$

Deze integraal kun je berekenen door het functievoorschrift y = $\sqrt{x}$ te herschrijven naar x = y².

De inhoud van het omwentelingslichaam wordt dan:
I = ${\displaystyle \underset{0}{\overset{2}{\int }}\text{π}{(y^2)}^2\text{d}y}$ = ${\displaystyle \underset{0}{\overset{2}{\int }}\text{π}{y}^4\text{d}y}$ = ${\left[\frac{1}{5}\text{π}{y}^5\right]}_0^2$ = 6,4π

‡

Opgaven

1. In het eerste deel van de Uitleg zie je hoe je de inhoud kunt berekenen van het omwentelingslichaam dat ontstaat door een grafiek op een bepaald interval om de `x`-as te wentelen.
   Gegeven de functie `f(x) = 4 - x^2`. `V` is het vlakdeel ingesloten door de grafiek van `f` en de `x`-as. Bereken de inhoud van het omwentelingslichaam dat ontstaat door V om de x-as te wentelen.
   


2. Bekijk de vorige opgave nog eens. Het vlakdeel `V` wordt nu om de `y`-as gewenteld. In de rest van de Uitleg staat hoe je dat aanpakt.
   1. Laat zien, dat je de inhoud van het omwentelingslichaam dat zo ontstaat kunt berekenen met de integraal `int_0^4 pi(sqrt(4 - y))^2 text(d)y`.
   2. Bereken deze inhoud met behulp van primitiveren.

Theorie

Een figuur die ontstaat door het wentelen van een functie om een as heet een omwentelingslichaam.

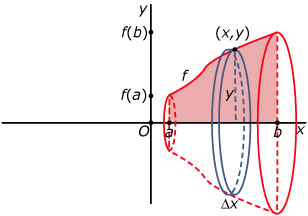
De inhoud I van het lichaam dat je krijgt als je de grafiek van de functie y = f(x) op het interval [a,b] wentelt om de x-as is:

I = ${\displaystyle \underset{a}{\overset{b}{\int }}\text{π}{y}^2\text{d}x}$ = ${\displaystyle \underset{a}{\overset{b}{\int }}\text{π}{\left(f(x)\right)}^2\text{d}x}$

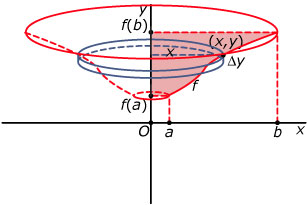
De inhoud I van het lichaam dat je krijgt als je de grafiek van de functie y = f(x) op het interval [a,b] wentelt om de y-as is:

I = ${\displaystyle \underset{f(a)}{\overset{f(b)}{\int }}\text{π}{x}^2\text{d}y}$ = ${\displaystyle \underset{f(a)}{\overset{f(b)}{\int }}\text{π}{\left(f^{\text{inv}}(y)\right)}^2\text{d}y}$
Hierin is f^inv de inverse functie is van f, de functie die ontstaat door y = f(x) te herschrijven tot x = f^inv(y).

‡

Voorbeeld 1

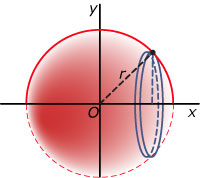
Een bol met straal r en middelpunt O ontstaat door de grafiek van f(x) = $\sqrt{r^2-x^2}$ op het interval [–r,r] om de x-as te wentelen.
Stel een formule op voor de inhoud en één voor de oppervlakte van die bol.

Antwoord

Voor de inhoud van de bol geldt:
I(bol) = ${{\displaystyle \underset{-r}{\overset{r}{\int }}\text{π}\left(\sqrt{r^2-x^2}\right)}}^2\text{d}x$ = ${\displaystyle \underset{-r}{\overset{r}{\int }}\text{π(}{r}^2-x^2)}\text{d}x$ = $\frac{4}{3}$πr³

De oppervlakte A(r) van de bol kun je uit I(r) afleiden.
Bedenk, dat bij toename van r met een heel klein beetje Δr = h de inhoud toeneemt met I(r + h) – I(r). De oppervlakte van deze laag met een dikte h is ongeveer de gevraagde oppervlakte en gelijk aan $\frac{I(r+h)-I(r)}{h}$.
Deze benadering wordt beter naarmate h naar 0 nadert.
En daarom is A(r) = $\underset{h\to 0}{\lim }\frac{I(r+h)-I(r)}{h}$ = I'(r).
Dit betekent dat de oppervlakte van de bol is: A(r) = 4πr².

‡

Voorbeeld 2

Hier zie je het vlakdeel(tje) ingesloten door de grafieken van
f(x) = 4 – x² en g(x) = 4 – x.
Bereken de inhoud van het omwentelingslichaam dat ontstaat door V om de x-as te wentelen.

Antwoord

Eerst bereken je de snijpunten van de grafieken: (0,4) en (1,3).

Vervolgens constateer je dat het omwentelingslichaam een soort van ring wordt: uit het lichaam dat ontstaat door de grafiek van f op [0,1] om de x-as te wentelen wordt het lichaam dat ontstaat door de grafiek van g op [0,1] om de x-as te wentelen weg geboord.
De gevraagde inhoud is daarom:
I = ${\displaystyle \underset{0}{\overset{1}{\int }}\text{π}{(4-x^2)}^2\text{d}x}$ – ${\displaystyle \underset{0}{\overset{1}{\int }}\text{π}{(4-x)}^2\text{d}x}$

Door haakjes uitwerken en primitiveren vind je: I = 1,2π.

‡

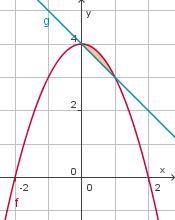
Voorbeeld 3

Hier zie je het vlakdeel(tje) ingesloten door de grafieken van
f(x) = 4 – x² en g(x) = 4 – x.
Bereken de inhoud van het omwentelingslichaam dat ontstaat door V om de y-as te wentelen.

Antwoord

Eerst bereken je de snijpunten van de grafieken: (0,4) en (1,3).

Vervolgens constateer je dat het omwentelingslichaam een soort van hoedje wordt: uit het lichaam dat ontstaat door de grafiek van f op [f(0),f(1)] om de y-as te wentelen wordt de kegel die ontstaat door de grafiek van g op [g(0),g(1)] om de y-as te wentelen weg geboord.
Vervolgens moet je van beide functies de inverse bepalen:

• f(x) = y = 4 – x² wordt: x = $\sqrt{4-y}$
• g(x) = y = 4 – x wordt: x = 4 – y

De gevraagde inhoud is daarom: I = ${\displaystyle \underset{3}{\overset{4}{\int }}\text{π}{\left(\sqrt{4-y}\right)}^2\text{d}y}$ – ${\displaystyle \underset{3}{\overset{4}{\int }}\text{π}{(4-y)}^2\text{d}y}$
Door haakjes uitwerken en primitiveren vind je: I = $\frac{1}{6}$π.

‡

Opgaven

3. In Voorbeeld 1 wordt de inhoud van een bol met straal `r` berekend. Je kunt op dezelfde manier een formule opstellen voor de inhoud van een kegel met straal `r` en hoogte `h`. Je begint dan met de lijn `y = r/h x` op het interval `[0,h]` en wentelt het vlakdeel ingesloten door die lijn, de `x`-as en de lijn `x = h` om de `x`-as.
   1. Leg uit waarom de hierboven gegeven vergelijking geschikt is voor de beschreven kegel.
   2. Stel nu door primitiveren een formule op voor de inhoud van de kegel.
   3. Stel ook door primitiveren een formule op voor de inhoud van een cilinder met straal `r` en hoogte `h`.


4. In Voorbeeld 1 wordt ook een formule afgeleid voor de oppervlakte van een bol met straal `r`.
   1. Hoe volgt de formule voor de oppervlakte van een bol uit die voor de inhoud?
   2. Waarom lukt dit niet bij de kegel en de cilinder? Hoe kun je daar toch de oppervlakte van berekenen?


5. Bestudeer nu eerst Voorbeeld 2.
   1. Schets het omwentelingslichaam dat ontstaat door `V` om de `x`-as te wentelen.
   2. Bereken nu zelf door haakjes uitwerken en primitiveren de inhoud van het omwentelingslichaam.
   3. Waarom is het niet mogelijk om de inhoud van dit lichaam te berekenen met `int_0^1 pi(f(x) - g(x))^2 text(d)x`?


6. Bestudeer nu eerst Voorbeeld 3.
   1. Schets het omwentelingslichaam dat ontstaat door `V` om de `y`-as te wentelen.
   2. Bereken nu zelf door haakjes uitwerken en primitiveren de inhoud van het omwentelingslichaam.

Verwerken

7. Bereken met behulp van primitiveren de inhoud van de omwentelingslichamen, die ontstaan bij wenteling om de `x`-as van de vlakdelen, begrensd door:
   1. de `x`-as en de grafiek van de functie `f(x) = x^2 - 7x + 6`;
   2. de `x`-as, de `y`-as en de grafiek van de functie `f(x) = x + 4 - 4sqrt(x)`;
   3. de `x`-as, de grafiek van de functie `f(x) = 8/x` en de lijnen `x = 2` en `x = 4`.


8. Bereken met behulp van primitiveren de inhoud van de omwentelingslichamen, die ontstaan bij wenteling om de `y`-as van de figuren, begrensd door:
   1. de grafiek van de functie `f(x) = x^3`, de `y`-as en de lijn `y = 4`;
   2. de `y`-as, de grafiek van de functie `f(x) = 0,5x^2 + 8` en een raaklijn uit `O` aan de grafiek van `f`.


9. Gegeven is de functie `f(x) = x + 3 - 4 sqrt(x)`.
   `V` is het vlakdeel begrensd door de grafiek van `f` en de lijn `y = 3`.
   Bereken exact de inhoud van het lichaam dat ontstaat door `V` te wentelen om de lijn `y = 3`.
   


10. Gegeven zijn de functies `f(x) = 6 - (x - 2)^2` en `g(x) = x^2 - 2x + 2`.
    `G` is het gebied dat door beide grafieken wordt ingesloten.
    1. Bereken exact de oppervlakte van `G`.
    2. `G` wordt om de `x`-as gewenteld. Bereken exact de inhoud van het omwentelingslichaam dat zo ontstaat.


11. Een bol ontstaat door de functie `f(x) = sqrt(r^2 - x^2)` om de `x`-as te wentelen op het interval `[-r,r]`.
    Neem nu het positieve getal `a` en neem aan dat `a < r`.
    1. Je wentelt het gebied ingesloten door de grafiek van `f`, de `x`-as en de lijn `x = a` om de `x`-as. Het lichaam dat zo onstaat heet een bolsegment. Stel met behulp van primitiveren een formule op voor de inhoud van zo'n bolsegment.
    2. Wanneer je aan het bolsegment een kegel toevoegt met de top in `O(0,0)`, hoogte `a` en straal `sqrt(r^2 - a^2)` dan heb je een bolsector. Stel met behulp van primitiveren een formule op voor de inhoud van zo'n bolsector.


12. Gegeven is de functie `f` met `f(x) = sqrt(x)`.
    De lijn met vergelijking `x = p` snijdt de grafiek van `f` in `A`. De lijn `y = q` gaat door `A`.
    `V` is het vlakdeel dat wordt begrensd door de grafiek van `f`, de `x`-as en de lijn `x = p`.
    `W` is het vlakdeel dat wordt begrensd door de grafiek van `f`, de `y`-as en de lijn `y = q`.
    De inhoud van het omwentelingslichaam dat onstaat door `V` om de `x`-as te wentelen is gelijk aan de inhoud die ontstaat door `W` om de `y`-as te wentelen.
    Bereken `p`.
    

Testen

13. Gegeven is de functie `f` door `f(x) = 2 - 2/(x^2)` .
    1. Bereken de nulpunten en de asymptoten van `f` en schets de grafiek van `f`.
    2. `V` is het vlakdeel ingesloten door de grafiek van `f`, de lijn `y = x` en de lijnen `x = 1` en `x = 3`. Bereken exact de oppervlakte van `V`.
    3. `V` wordt gewenteld om de `x`-as. Bereken exact de inhoud van het omwentelingslichaam dat zo ontstaat.


14. Gegeven zijn de functies `f(x) - 4 - x sqrt(x)` en `g(x) = 2`.
    `G` is het gebied dat wordt ingesloten door beide grafieken en de `y`-as. Dit vlakdeel wordt om de `y`-as gewenteld.
    Bereken exact de inhoud van het lichaam dat daardoor ontstaat.