Oppervlakte en lengte

Inleiding

Al in de tijd van de Oude Grieken was het berekenen van de exacte omtrek en de exacte oppervlakte van een cirkel een "hot item". Zij ontwikkelden daar methoden voor, maar pas in de 17de eeuw bedachten Isaac Newton en Gottfried Wilhelm Leibniz er onafhankelijk van elkaar een structurele methode voor. Dit was het begin van de integraalrekening.
En hebben zij dan het probleem van het berekenen van de omtrek en de oppervlakte van de cirkel ook opgelost?

Je leert nu:

• oppervlaktes ingesloten door lijnen en grafieken van functies berekenen;
• de lengte van een deel van de grafiek van een functie berekenen.

Je kunt al:

• integralen bepalen met behulp van primitiveren;
• integralen bepalen met behulp van je grafische rekenmachine.

Verkennen

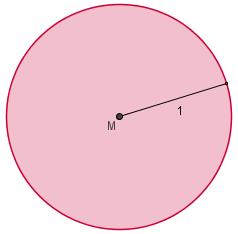
Als je deze cirkel in een xy-assenstelsel plaatst met punt M in de oorsprong, dan geldt voor elk punt op deze cirkel x² + y² = 1.
Je kunt daarom de cirkel beschrijven met twee functievoorschriften.

> Welke twee functievoorschriften?
> Hoe kun je nu de oppervlakte van deze cirkel bepalen?
> Ga na, dat de oppervlakte van de cirkel (ongeveer) gelijk is aan π.
> En kun je iets verzinnen voor het berekenen van de omtrek van deze cirkel?

Uitleg

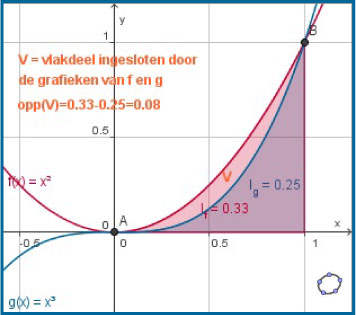
Je ziet hier het vlakdeel V ingesloten door de grafieken van f(x) = x² en g(x) = x³.
De oppervlakte van dit vlakdeel vind je door de integraal van f op [0,1] en de integraal van g op [0,1] van elkaar af te trekken:
opp(V) = ${\displaystyle \underset{0}{\overset{1}{\int }}f(x)\text{d}x}$ – ${\displaystyle \underset{0}{\overset{1}{\int }}g(x)\text{d}x}$.
Vanwege de somregel voor integreren kun je dit schrijven als:
opp(V) = ${\displaystyle \underset{0}{\overset{1}{\int }}(f(x)-g(x))\text{d}x}$
Deze wijze van oppervlakteberekening kun je heel algemeen toepassen.
Geldt op een bepaald interval [a,b] dat f(x) ≥ g(x), dan is de oppervlakte van het vlakdeel V dat door beide grafieken wordt ingesloten op dat interval gelijk aan:
opp(V) = ${\displaystyle \underset{a}{\overset{b}{\int }}(f(x)-g(x))\text{d}x}$
Of de grafieken onder of boven de x-as liggen, maakt daarbij niet uit.

Wil je ook de omtrek van V berekenen, dan moet je de lengte van de grafiek van f op [0,1] en die van de grafiek van g op [0,1] optellen. Maar hoe bereken je zo'n lengte?

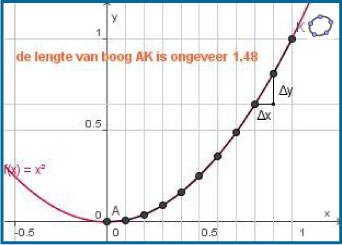
De lengte L van de grafiek van f(x) = x² op [0,1] wordt benaderd door dit interval op te delen in deelintervallen met een breedte van Δx. Op elk deelinterval heeft de grafiek een beginpunt en een eindpunt, het lijnstukje tussen beide benadert de grafiek steeds beter naarmate Δx naar 0 nadert. Als je de lengtes van al die lijnstukjes optelt, krijg je een benadering van L:

L ≈ ${\displaystyle \sum _{k=1}^n\sqrt{{(\Delta x)}^2+{(\Delta y_k)}^2}={\displaystyle \sum _{k=1}^n\sqrt{1+{\left(\frac{\Delta y_k}{\Delta x}\right)}^2}\cdot \Delta x}}$

Laat je nu Δx steeds dichter naar 0 naderen, dan nadert $\frac{\Delta y_k}{\Delta x}$ naar f'(x_k).
De Riemannsom gaat dan over in: L = ${\displaystyle \underset{0}{\overset{1}{\int }}\sqrt{1+{(f\text{'}(x))}^2}\text{d}x}$
Omdat f'(x) = 2x wordt dit: L = ${\displaystyle \underset{0}{\overset{1}{\int }}\sqrt{1+4x^2}\text{d}x}$ ≈ 1,47894...

‡

Opgaven

1. Het berekenen van de oppervlakte van een gebied dat wordt ingesloten door twee of meer krommen (of rechten) kun je met behulp van integreren berekenen. In de Uitleg zie je hoe dit in zijn werk gaat bij het gebied ingesloten door de grafieken van `f(x) = x^2` en `g(x) = x^3`.
   1. Bereken de oppervlakte van het gebied dat wordt ingesloten door de grafieken van `f` en `g` en de lijn `x = 2`.
   2. Bereken de oppervlakte van het gebied dat wordt ingesloten door de grafieken van `f` en `g` en de lijn `y = 2`.


2. Bestudeer hoe in de Uitleg de lengte van een grafiek met behulp van integreren kan worden berekend.
   1. Waar komt de uitdrukking `(Delta x)^2 + (Delta y)^2` in de Riemannsom vandaan?
   2. Neem `Delta x = 0,1` en bereken de bijbehorende Riemannsom.
   3. Controleer zelf de benadering van de lengte van de grafiek van `f(x) = x^2` op het interval `[0,1]` met behulp van de grafische rekenmachine.
   4. Bereken ook de lengte van de grafiek van `g(x) = x^3` op `[0,1]`.

Theorie

Bij het berekenen van oppervlaktes en lengtes kun je gebruik maken van integralen (neem telkens aan dat f op [a,b] bestaat en differentieerbaar is):

• Geldt op [a,b] dat f(x) ≥ 0, dan is de oppervlakte van het vlakdeel V tussen de grafiek van f en de x-as op dat interval gelijk aan:
  opp(V) = ${\displaystyle \underset{a}{\overset{b}{\int }}f(x)\text{d}x}$
  Is f(x) ≤ 0 op [a,b], dan is: opp(V) = ${\displaystyle \underset{a}{\overset{b}{\int }}-f(x)\text{d}x}$

• Geldt op [a,b] dat f(x) ≥ g(x), dan is de oppervlakte van het vlakdeel V dat door beide grafieken wordt ingesloten op dat interval gelijk aan:
  opp(V) = ${\displaystyle \underset{a}{\overset{b}{\int }}(f(x)-g(x))\text{d}x}$

• De booglengte van de grafiek van f op interval [a,b] is:
  L = ${\displaystyle \underset{0}{\overset{1}{\int }}\sqrt{1+{(f\text{'}(x))}^2}\text{d}x}$

‡

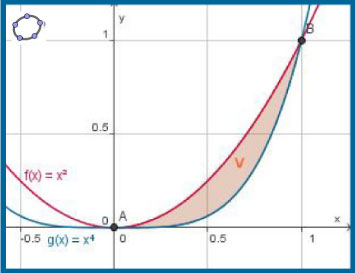
Voorbeeld 1

Bereken de oppervlakte van het vlakdeel V ingesloten door de grafieken van f(x) = x² en g(x) = x⁴ op het interval [0,1].

Antwoord

opp(V) = ${\displaystyle \underset{0}{\overset{1}{\int }}(x^2-x^4)\text{d}x}$ =
           = ${\left[\frac{1}{3}{x}^3-\frac{1}{4}{x}^4\right]}_0^1$ = $\frac{1}{12}$

‡

Voorbeeld 2

Bereken de omtrek van het vlakdeel V ingesloten door de grafieken van f(x) = x² en g(x) = x⁴ op het interval [0,1]. Geef een benadering in drie decimalen nauwkeurig.

Antwoord

De omtrek van V is de som van de lengte L_f van de grafiek van f op interval [0,1] en de lengte L_g van de grafiek van g op datzelfde interval.
Nu is f'(x) = 2x en g(x) = 4x³.
En dus is de omtrek van V:

L_f + L_g = ${\displaystyle \underset{0}{\overset{1}{\int }}\sqrt{1+{(2x)}^2}}\text{d}x+{\displaystyle \underset{0}{\overset{1}{\int }}\sqrt{1+{(4x^3)}^2}}\text{d}x$

Beide integralen zijn alleen met de grafische rekenmachine te bepalen.
Ga na dat de omtrek van V ongeveer 1,479 + 1,600 = 3,079.

‡

Voorbeeld 3

Bereken m.b.v. integreren de oppervlakte en de omtrek van de cirkel c met middelpunt O en straal 1 in twee decimalen nauwkeurig.

Antwoord

Omdat voor elk punt van de cirkel geldt x² + y² = 1, kun je hem beschrijven met twee functies: y₁ = $\sqrt{1-x^2}$ en y₂ = –$\sqrt{1-x^2}$.
Voor de berekening van oppervlakte en omtrek kijk je alleen naar de bovenste helft, dus y₁.

opp(c) = 2 · ${\displaystyle \underset{-1}{\overset{1}{\int }}\sqrt{1-x^2}}\text{d}x$ ≈ 3,14.

L(c) = 2 · ${\displaystyle \underset{-1}{\overset{1}{\int }}\sqrt{1+{\left(\frac{-x}{\sqrt{1-x^2}}\right)}^2}}\text{d}x={\displaystyle \underset{-1}{\overset{1}{\int }}\sqrt{1+\frac{x^2}{1-x^2}}\text{d}x}$ ≈ 6,28.

Denk er om dat je niet hebt bewezen dat de oppervlakte π en de omtrek 2π is. Je hebt ze alleen benaderd met je GR. Je kunt met integreren ook gemakkelijk de oppervlakte van een deel van de cirkel berekenen...

‡

Opgaven

3. Gegeven zijn de functies `f(x) = 4 - x^2` en `g(x) = x + 2`.
   Bereken met behulp van primitiveren de oppervlakte van het vlakdeel `V` ingesloten door de grafieken van `f` en `g`. Bekijk eventueel eerst Voorbeeld 1.
   


4. Gegeven zijn de functies `f(x) = 4 - x^2` en `g(x) = x + 2`.
   1. Bereken lengte van de grafiek van `g` op het interval `[-2,1]` met behulp van integreren. Bekijk eventueel eerst Voorbeeld 2.
   2. Omdat de grafiek van `g` op `[-2,1]` een lijnstuk is, kun je deze lengte ook berekenen met behulp van meetkundige technieken. Ga na, dat je daarmee dezelfde uitkomst krijgt.
   3. Bereken nu de omtrek van het vlakdeel `V` ingesloten door de grafieken van beide functies.


5. In Voorbeeld 3 worden de oppervlakte en de omtrek van een cirkel met straal 1 berekend.
   1. Bereken met behulp van integraalrekening de oppervlakte van een cirkel met straal `2`.
   2. Bereken door integreren de oppervlakte van het vlakdeel ingesloten door de cirkel `x^2 + y^2 = 4` en de lijn `x = 1` in twee decimalen nauwkeurig.
   3. Bereken deze oppervlakte ook meetkundig.
   4. Benader door integreren de omtrek van een cirkel met straal 2. Ga na, dat je uitkomst overeen komt met de formule voor de omtrek van een cirkel.

Verwerken

6. De grafieken van de functies `f(x) = x^2 + 3x + 5` en `g(x) = -x^2 + 5x + 9` zijn parabolen.
   1. Bereken de oppervlakte van het gebied tussen beide parabolen.
   2. Bereken ook de oppervlakte van het vlakdeel dat wordt ingesloten door de grafieken van `f` en `g`, en de lijn `x = 4`.


7. Ten opzichte van rechthoekig assenstelsel `Oxy` is `K` de grafiek van de functie `f(x) = sqrt(3 - x)`.
   Er is een getal `a`, zo dat `K`, de `x`-as en de lijn `x = a` een vlakdeel begrenzen, waarvan de oppervlakte gelijk is aan 18. Bereken `a`.
   


8. Bereken de booglengte van de grafiek van de functie `f` op het gegeven interval:
   1. `f(x) = x^3 + 1/(12x)` op `[1,2]`
   2. `f(x) = x sqrt(x)` op `[1,4]`.


9. Gegeven is de functie `f(x) = x^4 - 13x^2 + 36`.
   1. Breng de grafiek van deze functie zo in beeld dat alle karakteristieken duidelijk te zien zijn.
   De grafiek van `f` en de `x`-as sluiten drie vlakdelen in. De grootste van die drie vlakdelen is `V`.
   2. Bereken door primitiveren de oppervlakte van `V`.
   3. De raaklijn aan de grafiek van `f` voor `x = 3`, de `y`-as en de grafiek van `f` sluiten een vakdeel `W` in. Bereken de oppervlakte daarvan.


10. Gegeven is de functie `f(x) = x + 1/(x)`.
    Bereken de oppervlakte van het vlakdeel ingesloten door de grafiek van `f` en de lijn `y = 2,5`.
    


11. Bekijk de grafieken van de functies `f(x) = (x^2 - 4)(2x + 1)` en `g(x) = x^2 - 4`. De lijn met vergelijking `x = p` met `-2 < p < 0` snijdt de grafiek van `f` in `A` en de grafiek van `g` in `B`.
    1. Bereken de waarden van `p` waarvoor de oppervlakte van driehoek `OAB` gelijk is aan 3.
    Met domein `RR` zijn nu voor elke `a > 0` gegeven de functies:

    `f_a(x) = (ax^2 - 4)(2x + 1)` en `g_a(x) = ax^2 - 4`.

    De grafieken van `f_a(x)` en `g_a(x)` hebben drie gemeenschappelijke punten en sluiten twee vlakdelen `V_1` en `V_2` in.
    2. Bewijs dat de oppervlakten van `V_1` en `V_2` gelijk zijn.


12. Gegeven is de functie `f(x) = x + 3 - 4 sqrt(x)` met domein `[0,rarr:)`.
    Ten opzichte van een assenstelsel `Oxy` is `K` de grafiek van `f`.
    1. Gebruik de rekenmachine om `K` te tekenen.
    2. Bereken de oppervlakte van de driehoek gevormd door de `x`-as en de raaklijnen aan `K` in de punten waar `K` de `x`-as snijdt.
    3. Gebruik de rekenmachine om de lengte van `K` tussen `x = 1` en `x = 9` te bepalen.

Testen

13. Gegeven is de functie `f` door `f(x) = 4 - 4/((x-3)^2)`.
    1. Bereken in de nulpunten van `f` en breng de grafiek zo in beeld dat alle karakteristieken zichtbaar zijn.
    2. De grafiek van de functie `f` en de beide coördinaatassen sluiten een gebied `G` in. Bereken door primitiveren de oppervlakte van `G`.
    3. Bereken de omtrek van `G` in twee decimalen nauwkeurig.


14. Gegeven zijn de functies `f(x) = 4 - x sqrt(x)` en `g(x) = 2`.
    1. Teken het gebied `G` dat door de grafieken van `f` en `g`, en de `y`-as wordt ingesloten.
    2. Bereken de oppervlakte van het gebied `G`.
    3. Bereken de lengte van de grafiek van `f` tussen `x = 1` en `x = 4`.