Integreren

Inleiding

Het berekenen van integralen door middel van primitiveren noem je wel integreren. Omdat primitiveren weinig anders is dan terugrekenen vanuit een afgeleide, spelen bij het integreren de differentieerregels een belangrijke rol. Bijvoorbeeld kun je er de somregel voor integralen uit afleiden en een regel die vaak de substitutieregel wordt genoemd. En uit de productregel leid je de methode van partieel integreren af. Met name deze laatste methode is geen verplichte leerstof voor vwo, je vind er iets over bij de Toepassingen in het Totaalbeeld van dit onderwerp.

Je leert nu:

• het begrip integreren en de hoofdstelling van de integraalrekening;
• een paar belangrijke integreerregels;
• integreren toepassen bij het berekenen van oppervlaktes onder de grafiek van een functie.

Je kunt al:

• alle differentieerregels gebruiken
• eenvoudige functies primitiveren;
• integralen bepalen met behulp van je grafische rekenmachine.

Verkennen

Bekijk de functie f met f(x) = $\frac{x}{{(1+x^2)}^3}$.
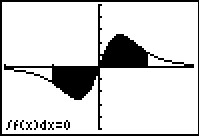Je kunt met je grafische rekenmachine gemakkelijk de intergraal van f op het intrval [–1,1] berekenen, uitkomst 0. Verder kun je de oppervlakte berekenen van het vlakdeel V ingesloten door de grafiek van f, de x-as en de lijnen x = –1 en x = 1.
Het gaat daarbij echter om (behoorlijk nauwkeurige) benaderingen...

> Probeer nu met behulp van primitiveren aan te tonen dat de oppervlakte van V exact 3/8 is.
TIP: Denk aan de kettingregel voor differentiëren.

Uitleg

Onder integreren versta je het berekenen van een integraal met behulp van primitiveren. Je maakt daarbij gebruik van de hoofdstelling van de integraalrekening, die zegt dat: ${\displaystyle \underset{a}{\overset{b}{\int }}f(x)\text{d}x}$ = F(b) – F(a) waarin F(x) een primitieve van f is.
Meestal noteer je F(b) – F(a) als ${\left[F(x)\right]}_a^b$.
De kunst hierbij is het vinden van F(x) door "omgekeerd differentiëren", door omkeren van de differentieerregels...

Bekijk de functie f met f(x) = $\frac{x}{{(1+x^2)}^3}$.
Je kunt met je GR gemakkelijk de integraal van f op het interval [–1,1] berekenen, uitkomst 0. Verder kun je de oppervlakte berekenen van het vlakdeel V ingesloten door de grafiek van f, de x-as en de lijnen x = –1 en x = 1. Het gaat daarbij echter om benaderingen... Wil je die oppervlakte exact bepalen, dan moet je een primitieve vinden van f(x) = x(1 + x²)^–3.
Het vinden van die primitieve kan door terugrekenen vanuit de kettingregel. Je moet dan herkennen, dat x = $\frac{1}{2}$ · 2x en dat 2x de afgeleide is van g(x) = 1 + x².
Dus is x(1 + x²)^–3 = $\frac{1}{2}$(g(x))^–3 · g'(x) en is de primitieve F(x) = $\frac{1}{2}$ · –$\frac{1}{2}$(g(x))^–2.
De oppervlakte van V is: 2 · ${\displaystyle \underset{0}{\overset{1}{\int }}\frac{x}{{(1+x^2)}^3}\text{d}x}$ = 2 · ${\left[-\frac{1}{4}{(1+x^2)}^{-2}\right]}_0^1$ = $\frac{3}{8}$.

‡

Opgaven

1. In de Uitleg wordt de hoofdstelling van de integraalrekening genoemd, maar niet bewezen. Een volledig bewijs hiervan valt ook buiten de leerstof voor het vwo. Maar enige toelichting is wel mogelijk.
   Je weet uit het voorgaande onderdeel dat als `F(x) = int_a^x f(t) text(d)t` geldt `F'(x) = f(x)`. Dat dit alleen opgaat voor mooie brave functies (aaneengesloten grafieken zonder verticale asymptoten) is niet ter sprake gekomen.
   1. Waarom moet `F(a) = 0`?
   2. Leg uit waarom `int_a^b f(t) text(d)t = F(b) - F(a)`
   3. Bereken met behulp van de hoofdstelling voor de integraalrekening `int_(-1)^1 x^2 text(d)x`.
   4. Welk probleem doet zich voor als je `int_(-1)^1 1/(x^2) text(d)x` wilt berekenen? Wat doet je grafische rekenmachine hiermee?


2. Bestudeer hoe in de Uitleg `int_0^1 x/((1 + x^2)^3) text(d)x` wordt berekend door primitieveren.
   1. Controleer de gevonden primitieve door differentiëren.
   2. Bereken op dezelfde manier `int_0^1 6x(1 + x^2)^3 text(d)x`.

Theorie

Onder integreren versta je het berekenen van een integraal met behulp van primitiveren. Je maakt daarbij gebruik van de hoofdstelling van de integraalrekening, die zegt dat: ${\displaystyle \underset{a}{\overset{b}{\int }}f(x)\text{d}x}$ = F(b) – F(a) waarin F(x) een primitieve van f is. Let er wel op dat de functie f geen verticale asymptoten mag hebben op het interval [a,b].
Meestal noteer je F(b) – F(a) als ${\left[F(x)\right]}_a^b$.
De kunst hierbij is natuurlijk het vinden van F(x) door "omgekeerd differentiëren".
Uit de differentieerregels kun je de volgende integreerregels afleiden:

• de constante-regel:
  ${\displaystyle \underset{a}{\overset{b}{\int }}k\cdot f(x)\text{d}x}=k\cdot {\displaystyle \underset{a}{\overset{b}{\int }}f(x)\text{d}x}$
• de somregel:
  ${\displaystyle \underset{a}{\overset{b}{\int }}(f(x)+g(x))\text{d}x}={\displaystyle \underset{a}{\overset{b}{\int }}f(x)\text{d}x}+{\displaystyle \underset{a}{\overset{b}{\int }}g(x)\text{d}x}$
• de substitutieregel (omgekeerde kettingregel):
  ${\displaystyle \underset{a}{\overset{b}{\int }}(f(g(x))\cdot g\text{'}(x))\text{d}x}={\left[F(g(x))\right]}_a^b$

‡

Voorbeeld 1

Gegeven is de functie f met f(x) = 0,5x⁴ – 4x².
Bereken met behulp van integreren de integraal van f op het interval [0,3].

Antwoord

Bij het primitiveren gebruik je in feite twee integreerregels: de constante-regel en de somregel. Maar waarschijnlijk let je daar nauwelijks op, een functie zoals dit is eenvoudig te primitiveren:
F(x) = 0,5 · $\frac{1}{5}$x⁵ – 4 · $\frac{1}{3}$x³ + c = $\frac{1}{10}$x⁵ – $\frac{4}{3}$x³ + c.

De gevraagde integraal is: ${\displaystyle \underset{0}{\overset{3}{\int }}f(x)\text{d}x}$ = ${\left[\frac{1}{10}{x}^5-\frac{4}{3}{x}^3+c\right]}_0^3$ = –11,7.

‡

Voorbeeld 2

Gegeven is de functie f met f(x) = 0,5x⁴ – 4x².
Bereken met behulp van integreren de oppervlakte van het vlakdeel begrensd door de grafiek van f op het interval [0,3], de x-as en de lijn x = 3.

Antwoord

Het primitiveren gaat als bij Voorbeeld 1: F(x) = $\frac{1}{10}$x⁵ – $\frac{4}{3}$x³ + c.

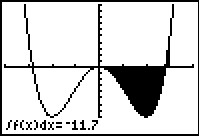
Voor het berekenen van de gewenste oppervlakte moet je nu de grafiek van f bekijken. Want bij een integraal leveren gebieden met negatieve functiewaarden ook een negatieve uitkomst op. In dit geval zie je dat er zowel een gebied met negatieve als een gebied met positieve functiewaarden is. Je berekent dus eerst de nulpunten van f. Ga na dat dat dit (–$\sqrt{8}$,0), (0,0) en ($\sqrt{8}$,0) zijn.
Voor de oppervlakte tel je nu twee integralen bij elkaar op:

opp(V) = ${\displaystyle \underset{0}{\overset{\sqrt{8}}{\int }}-f(x)\text{d}x+{\displaystyle \underset{\sqrt{8}}{\overset{3}{\int }}f(x)\text{d}x}}$

Ga nu zelf na dat de oppervlakte wordt: opp(V) = $\frac{128}{15}\sqrt{8}-\mathrm{11,7}$.

‡

Voorbeeld 3

Gegeven is de functie f met f(x) = $x\sqrt{4-x^2}$.
Bereken met behulp van integreren de oppervlakte van het vlakdeel begrensd door de grafiek van f en de x-as.

Antwoord

Voor het primitiveren van f kun je terugrekenen vanuit de kettingregel.
De afgeleide van g(x) = 4 – x² is g'(x) = –2x.
Als je x = –$\frac{1}{2}$ · –2x toepast, kun je de f schrijven als: f(x) = –$\frac{1}{2}$ · g'(x) · (g(x))^0,5.
En dus is F(x) = –$\frac{1}{2}$ · $\frac{1}{\mathrm{1,5}}$(g(x))^1,5 + c = $-\frac{1}{3}(4-x^2)\sqrt{4-x^2}$ + c.

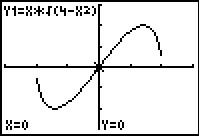
Met behulp van de grafiek zie je dat de gevraagde oppervlakte is:
opp(V) = $2\cdot {\displaystyle \underset{0}{\overset{2}{\int }}f(x)\text{d}x}=2\cdot {\left[-\frac{1}{3}(4-x^2)\sqrt{4-x^2}\right]}_0^2$ = $\frac{16}{3}$

‡

Opgaven

3. Bekijk in de Theorie wat je onder integreerregels verstaat.
   1. Gebruik de hoofdstelling van de integraalrekening om te laten zien dat de eerste twee integreerregels geldig zijn.
   2. Toon ook aan dat `int_a^b f(x) text(d)x + int_b^c f(x) text(d)x = int_a^c f(x) text(d)x`.


4. Gegeven is de functie `f(x) = x^3 - 6x^2 + 11x - 6`.
   1. Bereken de integraal van `f` over het interval `[1,3]`.
   2. Welke integreerregels heb je nu gebruikt? Bekijk eventueel Voorbeeld 1.
   3. Heb je met de integraal uit a de oppervlakte van een gebied berekend? Waarom?
   Breng nu de grafiek van `f` in beeld zo, dat je het gebied ingesloten door de grafiek van `f` en de `x`-as kunt zien.
   1. Welke nulpunten heeft `f`?
   2. Bereken nu de oppervlakte van het beschreven gebied. Bekijk eventueel eerst Voorbeeld 2.


5. Gegeven is de functie `f(x) = 1/4 x^4 - 2x^2 - 2 1/4`.
   1. Bereken de nulpunten van de functie `f`. Breng de grafiek van de functie in beeld.
   2. Bereken de oppervlakte van het gebied `V` dat ingesloten is door de grafiek van `f` en de `x`-as.
   3. De raaklijn aan de grafiek van `f` in het punt van `f` met x-coördinaat `3`, de `y`-as en de grafiek van `f` sluiten een gebied in. Bereken de oppervlakte daarvan.


6. De integraal `int_(-1)^1 sqrt(1 - x^2) text(d)x` kun je zien als de oppervlakte van een bepaald gebied.
   1. Welke vorm heeft dat gebied? Breng het in beeld met je grafische rekenmachine.
   2. Bepaal deze oppervlakte met de grafische rekenmachine.
   3. Waarom kun je deze oppervlakte niet exact berekenen met behulp van de tot nu toe genoemde integreerregels?
   4. Bereken de exacte oppervlakte van dit gebied met behulp van meetkundige kennis.


7. In Voorbeeld 3 wordt bij het integreren ook gebruik gemaakt van de substitutieregel.
   1. Loop het voorbeeld na.
   2. Bereken `int_(-1)^(1) x sqrt(1 - x^2) text(d)x`.
   3. Bereken de exacte oppervlakte van het gebied ingesloten door de grafiek van `f(x) = x sqrt(1 - x^2)` en de `x`-as.


8. De integraal `int_(1)^9 (1 + sqrt(x))/(sqrt(x)) text(d)x` kun je op twee manieren exact berekenen.
   1. Doe dit eerst door van de substitutieregel gebruik te maken.
   2. Je kunt dit ook doen door de deling uit te voeren. Laat zien dat je dan hetzelfde krijgt.

Verwerken

9. Bereken de volgende integralen exact en controleer de antwoorden met de grafische rekenmachine.
   1. `int_0^1 3/((2x + 1)^4) text(d)x`
   2. `int_0^1 x/((x^2 + 1)^4) text(d)x`
   3. `int_1^2 ((x + 1)^2)/(x^4) text(d)x`
   4. `int_(-3)^1 (-2)/(sqrt(3-2x)) text(d)x`


10. Gegeven is de functie `f(x) = 0,5(x - 4)(x^2 - 4)`.
    1. Breng de grafiek van deze functie zo in beeld dat alle karakteristieken duidelijk te zien zijn.
    2. Bereken de oppervlakte van het vlakdeel `V` ingesloten door de grafiek van `f` en de `x`-as.
    3. De raaklijn aan de grafiek van `f` voor `x = 2`, de `y`-as en de grafiek van `f` sluiten een vakdeel `W` in. Bereken de oppervlakte daarvan.


11. Gegeven is de functie `f(x) = 3x - x^3`.
    1. Bereken de oppervlakte van het gebied ingesloten door de grafiek van `f` en de `x`-as.
    2. Het gebied ingesloten door de grafiek van `f` en de `x`-as op het interval `[0,sqrt(3)]` wordt door de lijn `x = p` verdeeld in twee gebieden met gelijke oppervlakte. Bereken `p` in twee decimalen nauwkeurig.


12. Bereken de volgende onbepaalde integralen:
    1. `int (-(x - 3)(x + 1))/(x^4) text(d)x`
    2. `int (2x + 5)^3 sqrt(2x + 5) text(d)x`
    3. `int x^2 sqrt(6 - x^3) text(d)x`
    4. `int (x)/(sqrt(1 + x^2)) text(d)x`


13. Een heel eenvoudig voorbeeld van een functie die je wel kunt differentiëren, maar niet primitiveren is `f(x) = 1/x`.
    1. Welk probleem doet zich voor als je deze functie met de machtsregel wilt primitiveren?
    2. Bereken `int_1^4 1/x text(d)x`.
    3. Waarom heeft `int_(-1)^1 1/x text(d)x` geen betekenis? Zou je toch een waarde aan deze integraal kunnen toekennen? En zo ja, wat is dan je redenering?

Testen

14. Bereken de volgende integralen exact en controleer je antwoorden met de grafische rekenmachine.
    1. `int_0^1 root[5](3x + 1) text(d)x`
    2. `int_1^4 (2x^2 - 1)/(x^2) text(d)x`
    3. `int_(-1)^1 (4x)/((1 + x^2)^2) text(d)x`


15. Gegeven is de functie `f` door `f(x) = -2x + 3 * root[3](x^2)`.
    Bereken met behulp van primitiveren de oppervlakte van het vlakdeel ingesloten door de grafiek van `f` en de `x`-as in twee decimalen nauwkeurig.